Biot-Savart Law Formula, demonstrasjon, applikasjoner, øvelser

De Biot-Savart Law etablerer et forhold mellom magnetfeltet dB  på et punkt P, produsert av en tynn ledning som transporterer en strøm i og hvis differensiallengde er ds. Denne loven brukes til å finne magnetfeltet for nåværende fordelinger gjennom Superposisjonsprinsipp. 

Dette betyr at for å beregne det totale magnetfeltet på punkt P, må vi legge til alle bidragene som hver differensialdel Ds av ledningen bidrar. Og denne summen gjøres gjennom en integrert utført over hele gjeldende distribusjon.

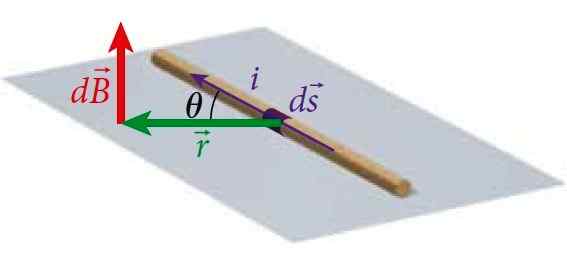
Figur 1. Et trådsegment transporterer en strøm I, som produserer et magnetfelt på et punkt P på en vis. Kilde: Bauer, W. Fysikk for ingeniørfag og vitenskap.

På denne måten kan du beregne feltet som produserer ledninger med strøm av forskjellige geometrier.

Biot-Savarts lov er oppkalt etter de to franske fysikerne som oppdaget det i 1820: Jean Marie Biot (1774-1862) og Felix Savart (1791-1841). For å oppnå dette, måtte de studere intensiteten og formen til magnetfeltet produsert av en rekke strømfordelinger.

[TOC]

Formel

Det matematiske uttrykket av biot-Savart-loven er som følger:

Den opprettholder analogier med tilsvarende for å beregne det elektriske feltet: Coulombs lov, bare at magnetfeltet dB I P er vinkelrett til flyet der ledningen er plassert. Vi kan se dette i figur 1.

Det forrige uttrykket kan også skrives som følger:

I begge uttrykk, r Det er posisjonsvektoren, rettet fra ID -strømelementets til det punktet hvor du vil beregne feltet.

Kan tjene deg: bevaring av det lineære momentumet: prinsipp, eksempler, øvelser.

For sin del, r Med en circumflejo -aksent er det den enhetlige vektoren som er rettet i samme retning og retning, men med en modul lik 1. Vektoren r Det er representert som følger:

Av denne grunn, ved å erstatte i forrige ligning -den som har r³ I nevneren- uttrykket er umiddelbart nådd² I nevneren.

I tillegg til de nevnte vektorene, inneholder formelen konstant μ_enten, anrop Vakuumpermeabilitet og hvis verdi er:

μ_enten = 4π x10^-7 T.m/ a.

Hvis vi ønsker å beregne magnetfeltvektoren, er det nødvendig å integrere all gjeldende distribusjon, som vi trenger dataene om dens geometri:

Vektorproduktet og høyre regel

Biot-Savart Law innebærer et vektorprodukt mellom ID-vektorers og r. Resultatet av et vektorprodukt mellom to vektorer er også en vektor.

I dette tilfellet ID -vektorproduktmodulens x r IS: (IDS) ⋅r⋅senθ, hvor θ er vinkelen mellom IDs og r, Som vist i figur 1.

På denne måten størrelsen på feltet dB Det er gitt av:

Retningen og betydningen kan bestemmes med regelen om høyre hånd, som er illustrert i denne figuren:

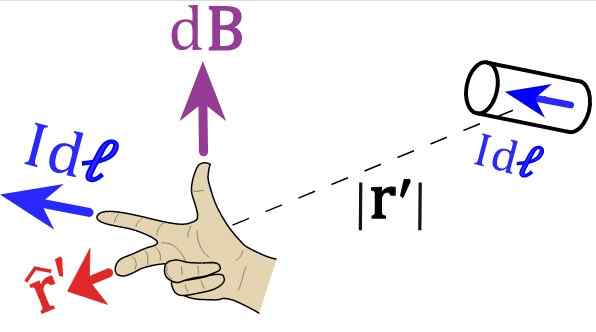Figur 2. Høyre håndregel for biot-Savart Law. Kilde: Wikimedia Commons.

Vi inviterer leseren til å plassere høyre hånd etter vektorene i figur 1 og 2. For figur 1 må pekefingeren peke til venstre, etter IDs eller idl, Langfingeren peker i henhold til vektoren r enhet.

Og til slutt er tommelen rettet opp, og dette er magnetfeltets retning.

Kan tjene deg: ellipsoid: egenskaper og eksempler

Demonstrasjon av Biot-Savart Law

Biot-Savart Law er fremtredende eksperimentell, noe som betyr at formuleringen kommer fra mange observasjoner om oppførselen til magnetfeltet produsert av nåværende ledninger.

Biot- og Savart -observasjoner

Dette var observasjonene fra franske forskere om magnetfeltet dB:

-Størrelsen på dB er omvendt proporsjonal med r².

-Det er også direkte proporsjonalt med størrelsen på det nåværende elementet, som kalles IDs Og også til sen θ, der θ er vinkelen mellom vektorene ds og r.

-dB er vinkelrett på begge ID -enes -Retningen til strømmen- som til r.

-Mangfoldig av dB er tangensiell for en radiokrets r Wire -sentrert. Med andre ord, felt B produsert av et nåværende segment består av konsentriske omkretser til den karrige.

-Betydningen der det dreier seg B Det er gitt av høyre tommelfingerregel: Den høyre tommelen er pekt i retning av strømmen, og de resterende fire fingrene er krøllet rundt ledningen, etter sirkulasjonen av feltet.

Alle disse observasjonene er kombinert i det matematiske uttrykket av loven som tidligere er beskrevet.

Biot-Savart Law Applications

Når den nåværende fordelingen har høy symmetri, kan integral enkelt løses, la oss se noen tilfeller:

Rettlinjet og tynn ledning

En rettlinjet ledning av lengde l transporterer en strøm i, for eksempel den som vises i figuren.

Det illustrerer den nødvendige geometrien for beregning av feltet. Dette er vinkelrett på papirarket, utgående til flyet hvis strømmen flyter fra venstre til høyre, og innkommende ellers (sjekk det med høyre rule).

Kan tjene deg: paramagnetisme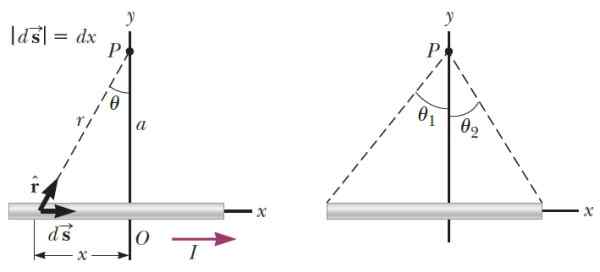Figur 3.- Til venstre geometrien som er nødvendig for å beregne magnetfeltet som produserer et tynt trådsegment på punkt P. Til høyre er vinklene som bestemmer plasseringen av P med hensyn til endene av segmentet. Kilde: Serway, R. Fysikk for vitenskap og ingeniørfag.

Være k  Enhetsvektoren i retning vinkelrett på planet, etter å ha utført prosessen med å integrere, magnetfeltet som ledningen produserer i P er:

Sirkulær spira

Radiosirkulære sløyfen til Den transporterer en strøm som vist på figuren og produserer et magnetfelt dB -i mørk grønn ved punkt P på den aksiale aksen, i en avstand x fra sentrum.

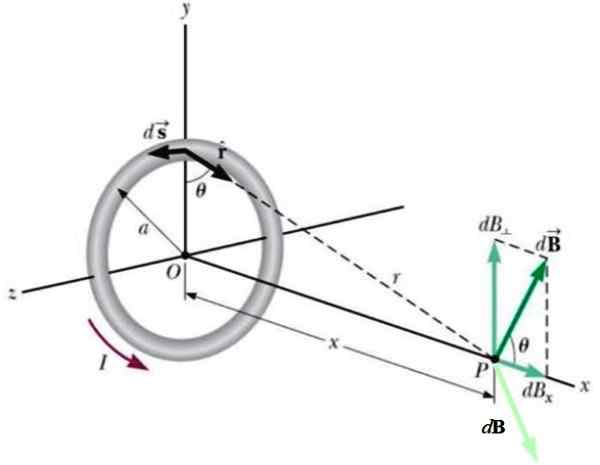Figur 4.- Geometri for beregning av feltet produsert av den sirkulære spasen ved punkt P på den aksiale aksen. Kilde: Wikimedia Commons.

Et annet nåværende element som ligger på motsatt side ville gi et annet bidrag til DB (lysegrønn), slik at den vertikale komponenten blir kansellert med den første.

Resultatet er at nettet magnetfeltet er horisontalt, så det er bare integrert i disse komponentene, noe som resulterer i:

Trening løst

Det er en ekstremt lang ledning som transporterer en strøm på 2 for å strømme som vist på bildet. Beregn størrelsen på magnetfeltet i en radiell avstand på 5 cm fra ledningen.

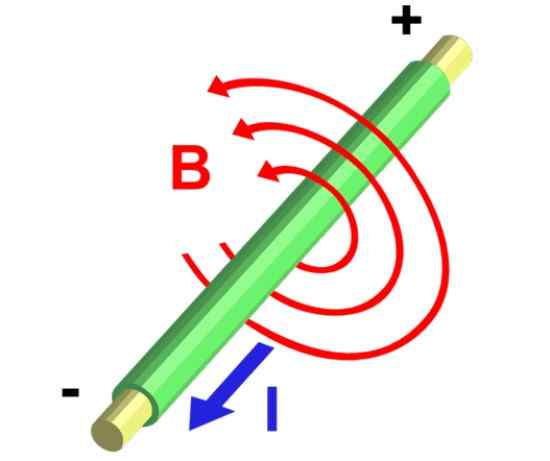Figur 5.- Magnetfeltlinjer i et rettlinjet trådsegment som transporterer strøm. Kilde: Wikimedia Commons.

Løsning

Siden det er en veldig lang ledning, kan vi ta uttrykket for det rettlinjede segmentet og lage θ₁= 0º og θ₂ = 180º for grensevinkler. Dette er nok for lengden på ledningen til å lagre uendelig.

På denne måten vil vi ha feltet:

Som forenkler:

Nå erstatter vi verdiene for uttalelsen:

I = 2 a

R = 5 x10^-2 m

μ_enten= 4π x10^-7 T.m/ a

Retningen og følelsen av B De er vist i figur 5, der retningen som forlater arket er tatt som k.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
6. Serway, r., Jewett, J. 2008. Fysikk for vitenskap og ingeniørfag. Volum 2. 7. Ed. Cengage Learning.