Hooke lovformler, eksempler, applikasjoner, øvelser

De Hooke's Law påpeker at deformasjonen som et elastisk objekt opplever, er direkte proporsjonal med den anvendte kraften på den. Proporsjonalitetskonstanten avhenger av objektets natur, dets geometri og materialet det er produsert.

Alle materialer har elastiske egenskaper i større eller mindre grad, så de overholder Hooke's lov når de kommer tilbake til sine opprinnelige dimensjoner, når styrken er opphører. Elastiske kilder og tannkjøtt er gode eksempler på gjenstander som er i samsvar med Hooke's Law, men det samme er stålkålene som er en del av en bro.

Figur 1. Hooke's Law om våren

Tar som et eksempel en fjær eller en ka. I følge Hooke's Law vil våren oppleve en X -deformasjon:

F ∝ x

Proporsjonalitetskonstanten, som, som en vår, kalles vårstivhet, Det er betegnet som k, derfor:

F = k⋅x

I enhetene i det internasjonale systemet kommer styrken i Newton (N) og deformasjonen i meter (m). Derfor har fjærkonstanten N/M -enheter. Fjærkonstanten representerer kraften som må påføres for å deformere den på 1 m i lengde.

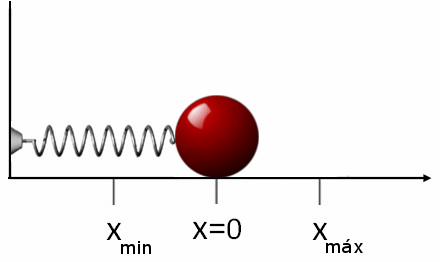Figur 2. Når våren er strukket, er kraften som utøves på objektet i strid med. Det samme skjer hvis våren krymper, i dette tilfellet driver den gjenstanden i motsatt forstand. Kilde: Wikimedia Commons.

Hvis den etter å ha trukket eller komprimert fjæren den frigjøres, vil den bevege seg i motsatt retning av den påførte kraften. Dette betyr at hvis vi strekker det, er det komprimert og omvendt. Det er grunnen til å styrke f_R at Vårøvelsene er:

F_R = -k⋅x

Det negative tegnet indikerer hva som blir sagt: at styrken motsetter seg forskyvning, så denne styrken er kjent som Gjenopprettende kraft.

[TOC]

Formel og ligninger

Forholdet mellom kraft og forskyvning i en vår ble oppdaget av Robert Hooke (1635-1703), en bemerkelsesverdig engelsk fysiker og kjent for sin rivalisering med Isaac Newton. Hooke var en allsidig forsker som med suksess dabbet i forskjellige vitenskapsfelt: mekanikk, biologi, astronomi og arkitektur.

Figur 3. Den engelske fysikeren Robert Hooke, som ikke kjenner datidens portretter. Dette er en gjenoppbygging laget av kunstneren Rita Gerer i 2004 gjennom beskrivelser som ble igjen av de som møtte forskeren. Kilde: Wikimedia Commons. Rita Greer / Fal.

Hooke innså at hvis styrken som brukes på en brygge ikke er veldig stor, er kaien proporsjonalt deformert for å tvinge, og når en gang nevnte kraft forsvinner, har våren sin naturlige lengde igjen.

Kan tjene deg: Jordens magnetosfære: Kjennetegn, struktur, gasser

På denne måten har Hooke's lov grafisk formen som en rett linje, hvis skråning er fjærkonstanten. Følgende bilde viser kraften som utøves på våren for å strekke den - eller komprimere den - avhengig av X -posisjonen. Merk at styrken ikke er avhengig av vårens naturlige lengde, men av dens forskyvning.

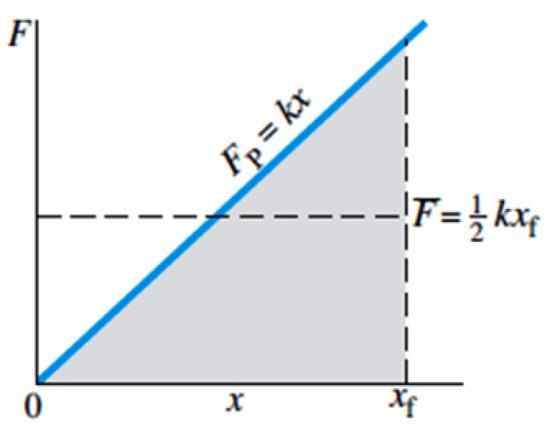Figur 4. Størrelsesorden f av nødvendig kraft for å strekke eller komprimere en fjær, avhengig av x -deformasjonen. Kilde: Giancoli, D. Fysikk med applikasjoner.

Gjennomsnittskraften er indikert i grafen med F med stolpe og tilsvarer ½ kx_F, hvor x_F er vårens endelige plassering.

Både kraften som utøves på våren, og kraften han utøver på et objekt bundet til ham, er varierende krefter. Jo mer du vil strekke deg eller komprimere til våren, jo mer styrke må du bruke for å kunne oppnå det.

Arbeid utført for å strekke eller komprimere en fjær

Når en kraft blir brukt som deformerer våren, blir et verk som er lagret om våren utført, og som kan brukes senere.

Mekanisk arbeid er definert som området under grafen for kraft F, avhengig av posisjon x. For å beregne arbeidet med at en variabel kraft f (x) gjør når du flytter et objekt fra posisjon x₁ til posisjon x₂ Det definerte integralet må beregnes:

I tilfelle av arbeidet som er nødvendig for å bringe en fjær fra likevektsposisjonen til posisjon x_F Det er veldig enkelt, siden området som skal beregnes er det for den grå skyggelagte trekanten i figur 4, hvis formel er kjent:

Trekantområde = ½ base. høyde

Derfor er det nødvendige arbeidet:

W = ½ x_F . (KX_F) = ½ k (x_F)²

Og hvis du vil beregne det nødvendige arbeidet for å bringe våren fra posisjon X til posisjon x_F, Det vil være likeverdig å beregne området for den ripete trapes i figur 5:

W = ½ k (x_F)² - ½ k x²

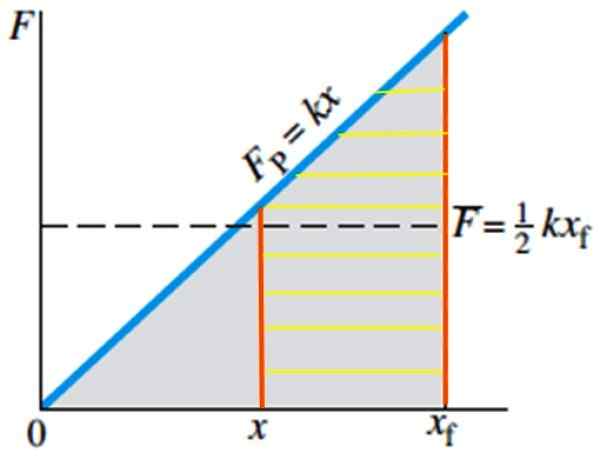Figur 5. Arbeidet som er gjort for å strekke våren fra posisjon X til XF -posisjonen som tilsvarer Rayada -området. Kilde: Giancoli, D. Fysikk med applikasjoner.

Eksempler på fjærer

I henhold til applikasjonen de er ment, kan fjærene være sylindrisk, konisk, spiral, med et sirkulært tverrsnitt (den vanligste), av firkantet eller rektangulær seksjon.

Kan tjene deg: elektriske ledere

En mye brukt klassifisering er i henhold til hvilken type innsats de vil bli utsatt for: det er torsjon, fleksjon, komprimering og forlengelsesfjærer. Sistnevnte brukes mye, og det fungerer også for spenning og komprimering.

Kompresjonsfjær

Et eksempel på kompresjonsfjær er det som brukes i leketøyet som heter Pogo enten Saltoín Palo. Disse fjærene lagrer en ganske potensiell energi når de komprimeres og frigjøres gradvis mens de går tilbake til likevektsposisjonen. På denne måten er ikke reboundene for brå.

Figur 6. Pogo eller Saltoín -pinne er basert på en kompresjonsfjær. Kilde: Wikimedia Commons.

Forlengelse og torsjonsfjærer

Våren for sprems er typen forlengelsesfjærer og er produsert med godt rollede svinger, med to kroker i endene. De er i stand til å beholde nok potensiell energi, som de senere frigjør når noen reiser seg og begynner å hoppe på lerretet, som også har sin egen elastiske respons, som alle materialer.

Torsjonsfjærer er veldig vanlige, fordi de tjener til å lage klærklemmer. I stedet for kroker i endene, bøyer de seg i vinkel, for å motstå kreftene som har en tendens til å utøve torsjon.

Figur 7. Fjærene er en del av utallige mekanismer, for eksempel disse klærne. Kilde: PXFuel.

Materialer for produksjonsfjærer

Det mest passende materialet å lage fjærer er de med en Ultimate motstand (endelig motstand), det vil si at de støtter en stor innsats før de bryter. Det er også praktisk at materialet har et høyt krypepunkt, slik at det ikke mister sine elastiske egenskaper med liten innsats.

INDUSTRIAL BRUK KJADER er produsert med legeringer som inkluderer stål med høyt karbon, kobber, nikkel og bronseinnhold.

Hooke's Law -søknader

Ettersom kildene har dyden med å lagre potensiell energi når de strekker seg eller komprimerer, er de i stand til å gjøre arbeid ved å flytte ting som mekanismer.

På denne måten har fjærene mange applikasjoner, fra små og daglige gjenstander, gjennom biler, til maskiner av alle slag. Fjærene tjener til:

-Sjokk vibrasjoner.

-Produserer uttrekkbare mekanismer: penn, hengende pinsett, hårkroker.

-Lage vår eller dynamometre

Og de er også en del av mekanismen til:

Kan tjene deg: lukket elektrisk krets

-Klokker.

-Trampoliner.

-Låser.

-Leker.

-Våpen.

-Nålmålere, for eksempel galvanometeret, som brukes til å måle strømmer, spenninger og motstand.

Løste øvelser

- Oppgave 1

En styrke i størrelsesorden 5 blir påført.0 n på en fjær, og lager en lengde på 3 strekk.5 cm fra sin naturlige lengde.

a) hvor mye som er strukket når den påførte kraften er 7 n?

b) Finn arbeidet utført av den påførte styrken for å strekke til våren 3.5 cm fra sin naturlige lengde.

Løsning på

Å vite at våren er strekk 3.5 cm gjennom påføring av 5.0 n vi kan beregne konstanten din:

k = f / x = 5.0 n / 3.5 cm = 1.43 N / cm.

Når en 7 n kraft påføres, oppnås følgende strekning:

x = f / k = 7.0 n / 1.43 N/m = 4.9 cm

Løsning b

Det nødvendige arbeidet for å deformere en fjær er gitt av:

W = ½ kx² = 0.5 x 1.43 N / cm x (3.5 cm)² = 8.76 n . CM = 8.76 n . 1 x10 ^-2 m = 0.0876 J.

- Oppgave 2

En vår med foraktelig deig og 10 cm lang henger fra en støtte. Hvis en masse på 2 kg henges, blir fjæren strukket til det når 15 cm. Regne ut:

a) Våren konstant

b) Vårstørrelsen når en masse på 3 kg er suspendert.

Løsning på

Vårstrekk er x = 15 - 10 cm = 5 cm

Siden systemet er i statisk likevekt, er kraften som utøves av våren når strekking rettes vertikalt oppover, for å kompensere for vekt, som er rettet ned, da:

F_R = W → kx = mg

K = 2 x 9.8 N / 5 X10 ^-2 M = 392 n/m

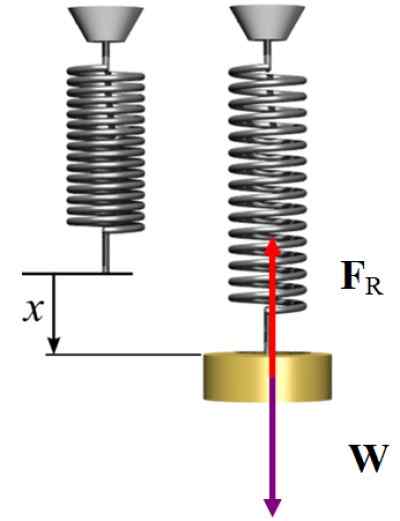Gratis kroppsdiagram for øvelsen løst 2. Kilde: Wikimedia Commons/F. Zapata.

Løsning b

Når en vekt på 3 kg er suspendert, er den nye kraften W = 3 x 9.8 n = 29.4 n

I dette tilfellet er strekningen:

x = mg /k = 29. 4 n / 392 n / m = 0.075 m = 7.5 cm

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Kreative mekanismer blogg. Fire forskjellige typer fjærer. Gjenopprettet fra: Creativemechanisms.com.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 2. Dynamisk. Redigert av Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed. Prentice Hall.
5. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming.  Pearson.