Lenz formel lov, ligninger, applikasjoner, eksempler

De Lenz Law Den slår fast at polariteten til den induserte elektromotoriske kraften i en lukket krets, på grunn av variasjonen i magnetfeltstrømmen, er slik at den motsetter seg variasjonen av nevnte strømning.

Det negative tegnet som blir satt i Faradays lov, tar hensyn til loven om Lenz, og er grunnen til at det kalles Faraday-Lenz Law og som er uttrykt som følger:

Figur 1. En toroidal spole er i stand til å indusere strømmer i andre drivere. Kilde: Pixabay.

[TOC]

Formler og ligninger

ε representerer den induserte elektromotoriske kraften, forkortet som Fem, Φ Det er magnetfeltstrømmen og t Det er tiden. Enheter i det internasjonale systemet (SI) for Fem De er volt (V).

For sin del magnetfeltet Φ Det er definert av følgende skalarprodukt:

Så mye B som n De er vektorstørrelser og kan betegnes med fet skrift eller med en pil på bokstaven. B Det er magnetfeltvektoren og n Det er enhetsvektoren (størrelsen lik 1) vinkelrett på overflaten krysset av B.

I ligningen vist B Den er konstant og enheten for Φ I SI for magnetfeltstrømmen er Weber (W):

1 Weber = 1 Tesla. måler²

En annen måte å uttrykke på Φ Det er den som er oppnådd ved å bruke definisjonen av skalarprodukt:

Φ = b.TIL.cos θ

I denne ligningen, B Det er størrelsen på magnetfeltet (uten fet eller pil, for å skille vektoren fra dens størrelse), er a området på overflaten krysset av feltet og θ er vinkelen mellom vektorene B og n.

Magnetfeltstrømmen kan varieres på forskjellige måter over tid, for å skape en Fem indusert i en sløyfe - en lukket krets - av areal til. For eksempel:

-Gjør magnetfeltet variabel over tid: B = B (T), Holder området og den konstante vinkelen, da:

-Spaseområdet kan variere, og la de andre størrelsene konstant:

 -Vinkelen mellom B Og overflaten varieres av rotasjonen av spasen, på denne måten oppnås en sinusformet generator:

Bedre ennå hvis i stedet for en enkelt sløyfe, brukes nougas, i så fall Fem Multipliser n ganger:

 Selvfølgelig kan magnetfeltstrømmen varieres med en hvilken som helst kombinasjon av disse formene, selv om det ville være noe mer komplisert å beskrive.

applikasjoner

Den umiddelbare anvendelsen av Lenzs lov er å bestemme betydningen av Fem eller indusert strøm uten behov for å utføre noen beregning. Tenk på følgende: Du har en løkke midt i et magnetfelt, for eksempel den som produserer en barmagnet.

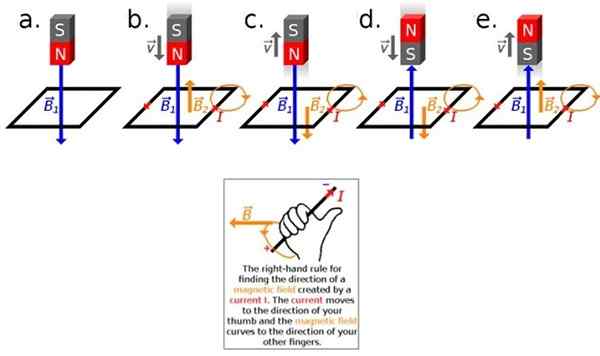
Figur 2. Anvendelse av Lenzs lov. Kilde: Wikimedia Commons.

Hvis magneten og sløyfen er i ro med hensyn til den andre, skjer det ingenting, det vil si at det ikke vil være noen indusert strøm, fordi magnetfeltstrømmen forblir konstant i så fall, (se figur 2A). For å indusere strøm er det nødvendig at strømmen varierer.

Nå, hvis det er en relativ bevegelse mellom magneten og spasen, enten fortrenger magneten mot spasen, eller er mot magneten, vil det være indusert strøm å måle (figur 2B og utover).

Dette induserte strømmen genererer på sin side et magnetfelt, derfor vil vi ha to felt: magneten B₁ i blått og den som er assosiert med strømmen som ble opprettet ved induksjon B₂, i oransje.

Høyre tommelen linjal lar deg vite retningen til B₂, For å gjøre dette plasseres tommelen på høyre hånd i retning og retning som strømmen har. De andre fire fingrene indikerer retningen som magnetfeltet er buet, ifølge figur 2 (nedenfor).

Kan tjene deg: konveks speil

Bevegelse av magneten gjennom spasen

La oss si at magneten blir droppet mot løkken med sin nordpol rettet mot den (figur 3). Magnetens feltlinjer forlater nordpolen N og kommer inn i sørens pol. Så det vil være endringer i φ, flyten skapt av B₁ som krysser sløyfen:Φ øker!  Derfor opprettes det i løkken et magnetfelt B₂ Med motsatt intensjon.

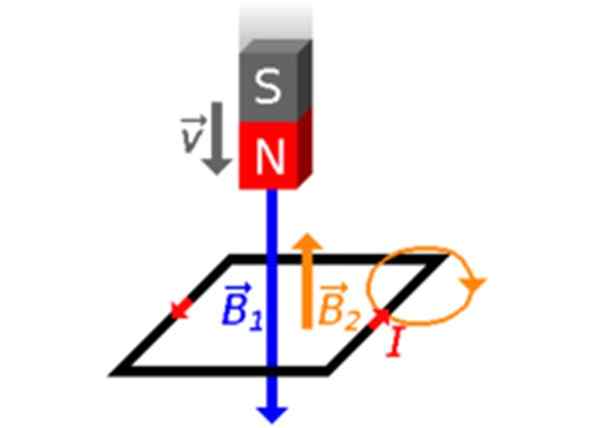Figur 3. Magneten beveger seg mot løkken med sin nordpol til henne. Kilde: Wikimedia Commons.

Den induserte strømmen gir en mening i strid med klokken nåler, -flekkaer røde i figurene 2 og 3-, i henhold til høyre tommelfingerregel.

La oss flytte bort spiras magnet og deretter hans Φ reduseres (figur 2c og 4), derfor er sløyfen rask med å lage et magnetfelt inne B₂ På samme måte, for å kompensere. Derfor er den induserte strømmen tid, som det kan sees i figur 4.

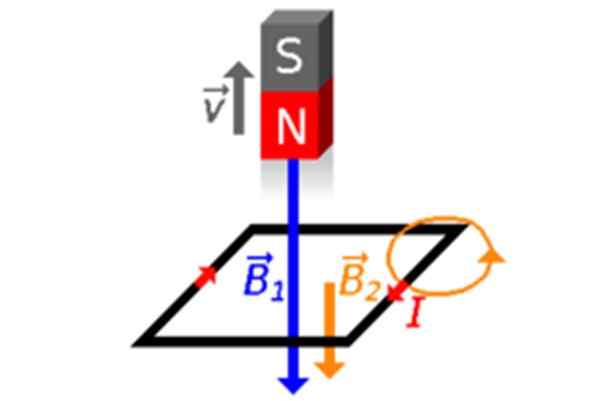Figur 4. Magneten beveger seg bort fra sløyfen, alltid med sin nordpol som peker på henne. Kilde: Wikimedia Commons.

Investerer magnetens plassering

Hva som skjer hvis magnetposisjonen er investert? Hvis sørpolen peker på løkken, peker feltet opp, siden linjene til B I en magnet forlater de nordpolen og kommer inn i Sydpolen (se figur 2D).

Umiddelbart informerer Lenzs lov at dette vertikale feltet opp, utfelling mot sløyfen, vil indusere et motsatt felt i dette, det vil si, B₂ ned og den induserte strømmen vil også være tid.

Til slutt beveger han seg bort magneten av La Espira, alltid med sin sørpol som peker på det indre av dette. Så inne i løkken er det et felt B₂ For å bidra til at magnetens fjerning ikke endrer feltstrømmen i den. Så mye B₁ som B₂ De vil ha samme betydning (se figur 2D).

Leseren vil innse at, som vi lovet, det er ikke blitt gjort noen beregninger for å vite retningen til den induserte strømmen.

Eksperimenter

Heinrich Lenz (1804-1865) utførte mange eksperimentelle verk gjennom hele sin vitenskapelige karriere. Det mest kjente er det vi nettopp har beskrevet, og dedikerer seg til å måle kreftene og magnetiske effekter skapt ved brått å slippe en magnet midt i en løkke. Med resultatene foredlet han arbeidet utført av Michael Faraday.

Dette negative tegnet i Faradays lov viser seg å være eksperimentet som det er mest anerkjent i dag. Imidlertid gjorde Lenz mange jobber innen geofysikk under ungdommen, og i mellomtiden var han dedikert til å slippe magneter inne i svingene og rørene. Han studerte også elektrisk motstand og metallkonduktivitet.

Spesielt på effekten av temperaturøkning i motstandsverdien. Han fortsatte å observere at når han varmet en ledning, reduseres motstanden og forsvinner varmen, noe James Joule også observerte uavhengig.

For alltid.

Kan tjene deg: Thévenin Theorem: Det som består av applikasjoner og eksempler

Lenzs rør

Det er et eksperiment der det demonstreres som en magnet stopper når den frigjøres inne i et kobberrør. Magneten når du faller, genererer variasjoner i magnetfeltet strømmen inne i røret, som tilfellet er med kraftspiralen.

Deretter opprettes en indusert strøm som motsetter seg endringen i strømmen. Røret lager sitt eget magnetfelt for dette, som vi allerede vet, er assosiert med den induserte strømmen. Anta at magneten frigjøres med Sydpolen ned, (2d og 5).

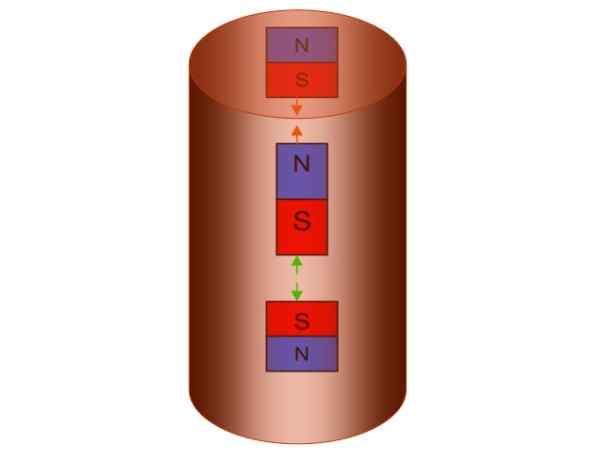Figur 5. Lenzs rør. Kilde: f. Zapata.

Som et resultat lager røret sitt eget magnetfelt med en nordpol ned og en sørpol oppover, som tilsvarer å lage et par fiktive magneter, en over og en annen under den som faller.

Konseptet er nedfelt i følgende figur, men det er nødvendig å huske at magnetiske stolper er uatskillelige. Hvis den nedre fiktive magneten har en nordpol ned, vil den nødvendigvis følge med sørover oppover.

Når de motsatte polene tiltrekker seg og motsetningene frastøter, vil magneten som faller bli frastøtt, og samtidig tiltrukket av den øvre fiktive magneten.

Nettoeffekten vil alltid være bremsing selv om magneten frigjøres med Nordpolen ned.

Joule-Lenz Law

Joule-Lenz-loven beskriver som en del av energien som er forbundet med den elektriske strømmen som sirkulerer av en sjåfør, går tapt i form av varme, en effekt som brukes i elektriske varmeovner, tallerkener, hårføner og elektrisk komfyr, blant andre apparater.

Alle av dem har en motstand, glødetråd eller varmeelement som varmer opp til passering av strømmen.

I matematisk form, det være seg R Motstanden til varmeelementet, Yo den nåværende intensiteten som sirkulerer gjennom den og t Tid, mengden varme produsert av Joule -effekten er:

Q = i². R. t

Hvor Q Det måles i Joules (SI -enheter). James Joule og Heinrich Lenz oppdaget denne effekten samtidig rundt 1842.

Eksempler

Nedenfor viser vi tre viktige eksempler der Faraday-Lenzs lov blir anvendt:

Vekselstrømgenerator

En vekselstrømgenerator transformerer mekanisk energi til elektrisk energi. Stiftelsen ble beskrevet i begynnelsen: en sløyfe roteres midt i et jevnt magnetfelt, for eksempel den som er opprettet mellom de to polene til en stor elektromagnet. Når det brukes N Spiraler, The Fem øker proporsjonalt med N.

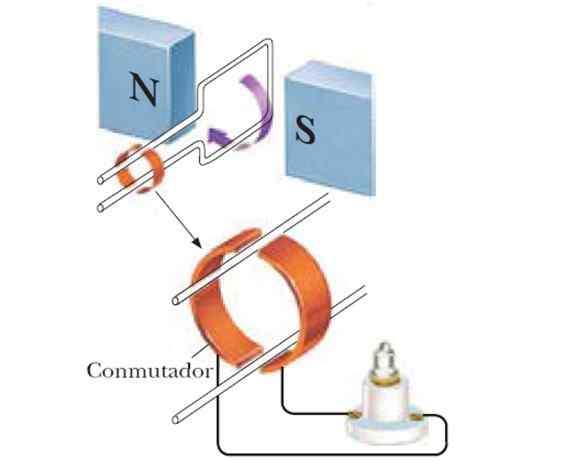Figur 6. Vekselstrømgeneratoren.

Når sløyfen dreies, endrer den normale vektoren til overflaten sin orientering med hensyn til feltet, og produserer en Fem som varierer på en sinusformet måte over tid. Anta at vinkelfrekvensen for rotasjon er Ω, Når du erstatter i ligningen som skjedde i begynnelsen, vil det være:

Transformatoren

Det er en enhet som lar deg få en direkte spenning fra en alternativ spenning. Transformatoren er en del av utallige enheter, for eksempel en mobiltelefonlader, for eksempel.Det fungerer på følgende måte:

Det er to spoler rullet rundt en jernkjerne, en kalles en hoved og den andre sekundær.  Det respektive antall runder er n₁ og n₂.

Primærspole eller vikling er koblet til en alternativ spenning (for eksempel hjemmelaget strøm, for eksempel) av skjemaet V_P = V₁.cos ωt, forårsaker en vekselfrekvensstrøm som sirkulerer Ω.

Denne strømmen har sin opprinnelse et magnetfelt som igjen forårsaker en oscillerende magnetisk fluks i den andre spolen eller viklingen, med en sekundær spenning av skjemaet V_S = V₂.cos ωt.

Imidlertid viser det seg at magnetfeltet inne i jernkjernen er proporsjonal med det omvendte av antall omganger av primærviklingen:

Det kan tjene deg: 13 eksempler på Newtons andre lov i hverdagen

B ∝ 1 /n₁

Og slik blir det V_P, spenningen i den primære viklingen, mens Fem indusert V_S I den andre viklingen er det proporsjonalt, som vi vet, til antall svinger n₂ Og også til V_P.

Så å kombinere disse proporsjonalitetene er det et forhold mellom V_S og V_P som avhenger av kvotienten mellom antall svinger på hver, som følger:

V_S = (N₂ /N₁) V_P

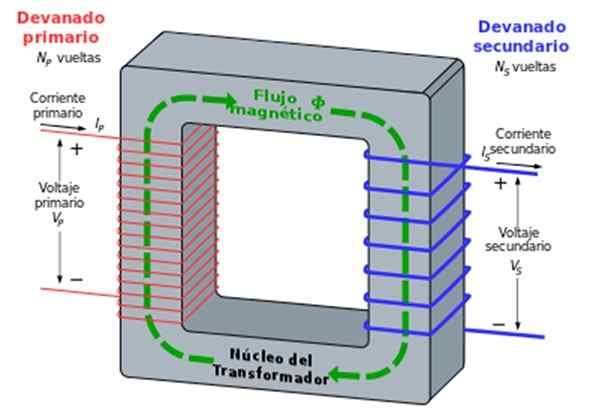Figur 7. Transformatoren. Kilde: Wikimedia Commons. Kundalinizero [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Metalldetektoren

De er enheter som brukes i banker og sikkerhetsflyplasser. De oppdager tilstedeværelsen av noe metall, ikke bare jern eller nikkel. De jobber takket være de induserte strømningene, gjennom bruk av to spoler: en sender og en annen mottaker.

En vekslende høyfrekvensstrøm føres i overføringsspolen, slik at den genererer et alternativt magnetfelt langs aksen (se figur), som induserer en strøm i mottaksspolen, noe mer eller mindre likt det som skjer med transformatoren.

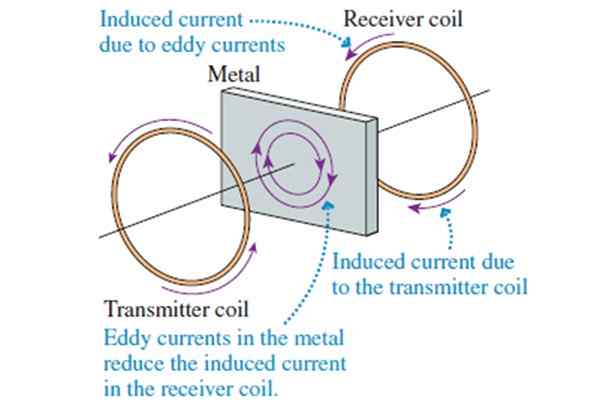Figur 8. Metalldetektoroperasjonsprinsipp.

Hvis et stykke metall er plassert mellom begge spoler, vises små induserte strømmer i det, kalt Foucault -strømmer (som ikke kan strømme i en isolator). Mottakende spole reagerer på magnetfeltene i overføringsspolen og de som er opprettet av Foucaults strømmer.

Foucault -strømmer prøver å minimere magnetfeltstrømmen i metallstykket. Derfor avtar feltet som oppfatter mottaksspolen, avtar når du interponerer et metallstykke mellom begge spoler. Når dette skjer en alarm som advarer tilstedeværelsen av et metall.

Øvelser

Oppgave 1

Det er en sirkulær spole med 250 firmaer på 5 cm radius, som ligger vinkelrett på et magnetfelt på 0.2 t. Bestem Fem indusert hvis i et tidsintervall på 0.1 s, det magnetiske magnetfeltet fungerer og indikerer betydningen av strømmen, i henhold til følgende figur:

Figur 9. Sirkulær spirra midt i et jevnt magnetfelt vinkelrett på spaseplanet. Kilde: f. Zapata.

Løsning

Først vil vi beregne størrelsen på den induserte FEM, deretter vil betydningen av den tilhørende strømmen bli indikert i henhold til tegningen.

N = 250 svinger

A = π. R² = s . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (Vektoren n Det tar parallelt med B)

Når magnetfeltet dobler størrelsesorden, har du:

Erstatte disse verdiene i ligningen for størrelsen på Fem Indusert:

ε = 250. 0.0079 m² . 2 t/s = 3.95 v

Siden feltet har doblet seg, er det også opprettet magnetfeltstrømmen, derfor opprettes en indusert strøm som motsetter seg en nevnte økning i løkken.

Feltet i figuren peker på skjermen. Feltet som er opprettet av den induserte strømmen, må forlate skjermen og bruke riktig tommelregel, det følger at den induserte strømmen er anti -Horary.

Oppgave 2

En firkantet vikling består av 40 svinger på 5 cm side, som svinger 50 Hz ofte midt i et ensartet størrelsesfelt 0.1 t. Opprinnelig er spolen vinkelrett på feltet. Hva vil være uttrykket for Fem indusert?

Løsning

Fra tidligere seksjoner ble dette uttrykket trukket ut:

ε = n.B.TIL. Ω. sin ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 spiraler

Ω = 2π.F = 2π.50 Hz = 100p s^-1

B = 0.1 t

ε = 40 x 0.1 x 0.0025 x 100π  X SEN 50.t =p . Sen 100π.TV

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
3. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. OpenX College. Faradays induksjonslov: Lenzs lov. Hentet fra: OpenTextBc.Ac.
5. FYSIKK LIBRETTEXTS. Lenzs lov. Gjenopprettet fra: Phys.Librettexts.org.
6. Sears, f. (2009). University Physics Vol. 2.