Tilleggsvinkler som er, beregning, eksempler, øvelser

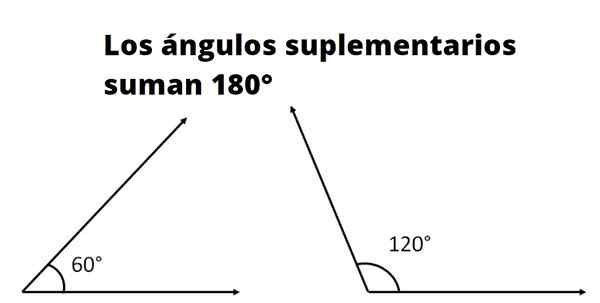
To eller flere er Supplerende vinkler Hvis summen av tiltakene tilsvarer målet på en flat vinkel. Målet på en flat vinkel, også kalt flat vinkel, i grader er 180º og i radianer er π.

For eksempel finner vi at de tre indre vinklene til en trekant er supplerende, siden summen av tiltakene er 180º. Tre vinkler er vist i figur 1. Fra ovenstående følger det at α og β er supplerende, siden de er tilstøtende og deres fulle sum en flat vinkel.

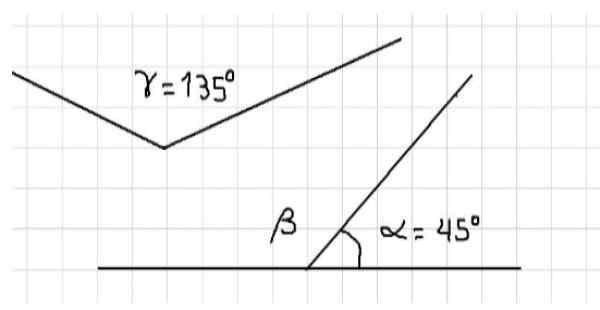
Figur 1: α og β er supplerende. α og γ er supplerende. Kilde: f. Zapata.

Også i den samme figuren er det vinkler α og γ som også er supplerende, fordi summen av tiltakene deres er lik omfanget av en flat vinkel, det vil si 180º. Det kan ikke sies at vinklene β og γ er supplerende fordi det begge er stumpe vinkler som er tiltakene er større enn 90º og derfor overstiger summen 180º.

Kilde: Lafer.com

På den annen side kan det sies at målet på vinkelen β er lik målet på vinkelen γ, siden hvis β er supplerende til α og γ er supplerende av α, så β = γ = 135º.

[TOC]

Eksempler

I de følgende eksempler blir det bedt om å finne de ukjente vinklene, angitt med avhør i figur 2. De spenner fra de enkleste eksemplene til noen litt mer forseggjorte enn leseren bør være mer forsiktige.

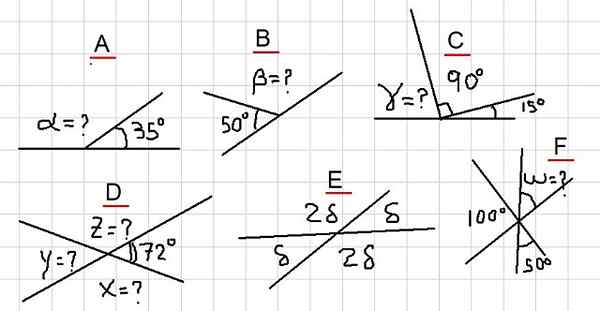Figur 2. Ulike eksempler på tilleggsvinkler. Kilde: f. Zapata.

Eksempel a

I figuren har vi at de tilstøtende vinklene α og 35º legger til en flat vinkel. Det vil si α + 35º = 180º og derfor er det oppfylt at: α = 180º- 35º = 145º.

Eksempel b

Ettersom β er supplerende med vinkelen på 50 º, blir det fulgt at β = 180º - 50º = 130º.

Kan tjene deg: Hva er elementene i lignelsen? (Deler)

Eksempel c

Fra figur 2C blir følgende sum lagt merke til: γ + 90º + 15º = 180º. Det vil si at y er supplerende med vinkel 105º = 90º + 15º + 15º. Det konkluderes da med at: 

γ = 180º- 105º = 75º

Eksempel d

Ettersom x er supplerende med 72º, følger det at x = 180º - 72º = 108º. I tillegg og det er supplerende med x, deretter y = 180º - 108º = 72º.

Og til slutt er z supplerende med 72º, derfor z = 180º - 72º = 108º.

Eksempel e

Vinklene Δ og 2Δ er supplerende, derfor Δ + 2Δ = 180º. Noe som betyr at 3δ = 180º, og dette igjen tillater skriving: Δ = 180º / 3 = 60º.

Eksempel f

Hvis vi kaller vinkelen mellom 100º og 50º, er det da nødvendig å bli supplert til dem, fordi det observeres at deres fulle sum en flat vinkel.

Det følger at u = 150º. Som u er motarbeidet av toppunktet til w, deretter w = u = 150º º.

Øvelser

Tre øvelser er foreslått nedenfor, i alle av dem må verdien av vinkler A og B finnes i grader, slik at forholdene vist i figur 3 er oppfylt. Konseptet med tilleggsvinkler brukes i oppløsningen av dem alle.

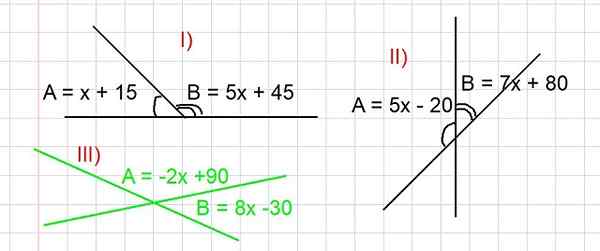Figur 3. Figur for å løse øvelser I, II og III i tilleggsvinkler. Alle vinkler kommer til uttrykk i grader. Kilde: f. Zapata.

- Øvelse I

Bestem verdiene til vinkler A og B i del I) i figur 3.

Løsning

A og B er supplerende, der a + b = 180 grader må erstattes, deretter erstattes uttrykket A og B som en funksjon av x, som det vises i bildet:

(x + 15) + (5x + 45) = 180

En første -bestill lineær ligning oppnås. For å løse det blir begrepene kastet: begrepene:

6 x + 60 = 180

Kan tjene deg: Real numre: Historie, eksempler, egenskaper, operasjoner

Å dele begge medlemmene mellom 6 er:

x + 10 = 30

Og til slutt å rydde, følger det at X er verdt 20º.

Nå må verdien av x erstattes for å finne de bestilte vinklene. Derfra må du vinkel A er: a = 20 +15 = 35º.

Og for sin del er vinkelen B = 5*20 + 45 = 145º.

- Øvelse II

Finn verdiene til vinkler A og B i del II) i figur 3.

Løsning

Som A og B er supplerende vinkler, A + B = 180 grader har. Erstatte uttrykket av a og b som en funksjon av x gitt i del II) i figur 3 er:

(-2x + 90) + (8x - 30) = 180

Igjen oppnås en første grads ligning, som begrepene må være praktisk gruppe:

6 x + 60 = 180

Å dele begge medlemmene mellom 6 er:

x + 10 = 30

Der det følger at X er verdt 20º.

Det vil si at vinkelen a = -2*20 + 90 = 50 °. Mens vinkel B = 8*20-30 = 130.

- Øvelse III

Bestem verdiene på vinkler A og B på del III) i figur 3 (i grønt).

Løsning

Som A og B er supplerende vinkler, A + B = 180 grader har. Uttrykket av A og B må erstattes som en funksjon av x gitt i figur 3, som du har:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Deling av begge medlemmene med 12 for å fjerne verdien av x, har du:

x + 5 = 15

Endelig er det funnet at X er verdt 10 grader.

Fortsett nå å erstatte for å finne vinkel a: a = 5*10 -20 = 30 °. Og for vinkel B: B = 7*10 + 80 = 150º

Kan tjene deg: Hva er statistikkområdet? (Med eksempler)

Supplerende vinkler i to paralleller kuttet av en secant

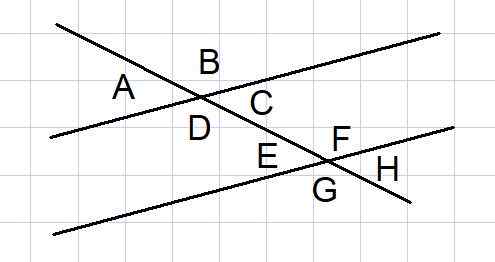Figur 4. Vinkler mellom to paralleller kuttet av en secant. Kilde: f. Zapata.

To parallelle linjer kuttet av en sikring er en vanlig geometrisk konstruksjon i noen problemer. Blant slike linjer dannes 8 vinkler som vist i figur 4.

Av de 8 vinklene er noen par vinkler supplerende, som vi viser nedenfor:

1. De ytre vinklene til og B, og det ytre g og h
2. Interiørvinklene d og C, og interiøret E og F
3. De ytre vinklene A og G, og den ytre B og H
4. De indre vinklene d og e, og de innsatte C og F

Ved fullstendighet blir også de like vinklene navngitt:

1. De interne vekslingene: d = f og c = e
2. De ytre vekslingene: a = h og b = g
3. De tilsvarende: a = e og c = h
4. Motsetningene etter toppunkt a = c og e = h
5. De tilsvarende: b = f og d = g
6. Motsetningene av Vertex B = D og F = G

- Øvelse IV

I referanse til figur 4, der vinklene viser mellom to parallelle linjer kuttet av en secant, bestemmer verdien av alle vinkler i radianer, vel vitende om at vinkelen a = π/6 radianer.

Løsning

A og B er supplerende ytre vinkler derfor b = π - a = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Referanser

1. Baldor, J. TIL. 1973.Flat og romgeometri. Sentralamerikansk kulturell. 
2. Matematiske lover og formler. Vinkelmålingssystemer. Hentet fra: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Gjenopprettet fra: Gutenberg.org.
4. Wikipedia. Supplerende vinkler. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Transportør. Gjenopprettet fra: er.Wikipedia.com
6. Zapata f. Goniometer: historie, deler, drift. Hentet fra: Lifer.com