Kepler -lover Forklaring, øvelser, eksperiment

De Kepler lover Om planeten ble formulert av den tyske astronomen Johannes Kepler (1571-1630). Kepler deducerte dem basert på arbeidet til læreren hans danske astronom Tycho Brahe (1546-1601).

Brahe samlet nøye dataene fra planetariske bevegelser over mer enn 20 år, med overraskende nøyaktighet og nøyaktighet, hvis det tas i betraktning at teleskopet ennå ikke var oppfunnet. Gyldigheten av dataene dine er fortsatt gyldig i dag.

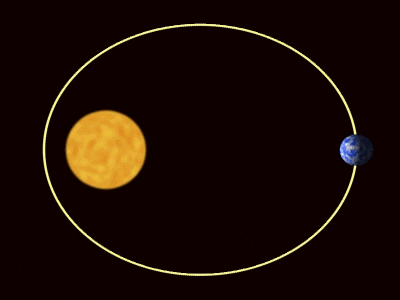Figur 1. Orbits for planetene i henhold til Keplers lover. Kilde: Wikimedia Commons. Willow/CC av (https: // creativecommons.Org/lisenser/av/3.0)

[TOC]

Keplers 3 lover

Keplers lover etablerer:

-Første lov: Alle planeter beskriver elliptiske baner med solen i et av søkelysene.

-Andre lov eller lov av det samme: En linje rettet fra sol til enhver planet (fokal radio), feie like områder i like tider.

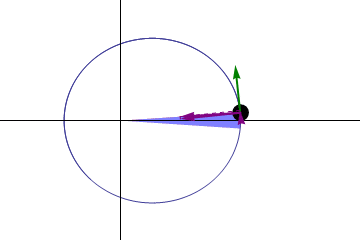Figur 2. Lov om områdene. Kilde: Wikimedia Commons. Gonfer/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)

-Tredje lov: Tidens kvadrat som tar enhver planet orbital rundt solen er proporsjonal med kuben i sin gjennomsnittlige avstand til solen.

Være T sa tid, ringte Orbital periode, og r Den gjennomsnittlige avstanden, da:

T² er proporsjonal med r³

T = k r³

Dette betyr at kvotienten T²/ r³ Det er det samme for alle planetene, noe som gjør det mulig å beregne orbitalradius, hvis orbitalperioden er kjent.

Når T Det kommer til uttrykk i år og r I astronomiske enheter ua*er proporsjonalitetskonstanten verdt k = 1:

T²= r³

*En astronomisk enhet tilsvarer 150 millioner kilometer, som er den gjennomsnittlige avstanden mellom jord og sol. Orbitalperioden på jorden er 1 år.

Universal Gravitation Law og Keplers tredje lov

Den universelle gravitasjonsloven slår fast at størrelsen på gravitasjonsattraksjonskraften mellom to masseobjekter M og m henholdsvis, hvis sentre er separate en avstand r, Det er gitt av:

F = g mm /r²

G er den universelle gravitasjonskonstanten og dens verdi er g = 6.674 x 10 ^-elleve N.m²/kg² .

Nå er planetene til planetene elliptiske med en veldig liten eksentrisitet.

Dette betyr at bane ikke beveger seg mye bort fra en sirkel, bortsett fra i noen tilfeller som dvergpluto. Hvis vi tilnærmer banene til den sirkulære formen, er akselerasjonen av planetens bevegelse:

til_c = v²/r

Gitt F = ma, ha:

G mm /r² = m.v²/r

Her v Det er planetens lineære hastighet rundt solen, statisk og masseforutsetning M, Mens planeten er m. Så:

Kan tjene deg: Viktige figurer: regler, eksempler, løste øvelser

Dette forklarer at planetene lengst fra solen har lavere orbitalhastighet, siden det avhenger av 1/√r.

Ettersom avstanden som planeten reiser er omtrent lengden på omkretsen: l = 2πr og det tar en lik tid t, orbitalperioden, oppnås den:

V = 2πr /t

Utjevning av begge uttrykkene for v Et gyldig uttrykk for t oppnås², Torget i orbitalperioden:

Og dette er nettopp Keplers tredje lov, siden parentesen i dette uttrykket 4π² /Gm Det er konstant, derfor T² er proporsjonal med avstand r forhøyet til kuben.

Den definitive ligningen for orbitalperioden oppnås ved å trekke ut kvadratrot:

Beregning av solens mass

Hvor mye er solens mass? Det er mulig å finne ut av denne ligningen. Vi vet at jordens orbitalperiode er ett år og orbitalradius er 1 UA, tilsvarer 150 millioner kilometer, så vi har alle nødvendige data.

I vår forrige ligning fjerner vi M, Men ikke før du konverterer alle verdier til det internasjonale systemet med enheter hvis:

1 år = 3.16 x 10⁷ sekunder.

1 ua = 150 millioner km = 1.5 x10^elleve m.

Og ved å erstatte dataene i ligningen, oppnår vi et ganske vellykket estimat av solens sol i 2.0 x 10 ³⁰ kg.

Øvelser

Selv om Kepler bare hadde planetene i tankene da han hentet sine berømte lover, er disse også gyldige for bevegelse av satellitter og de andre kroppene i solsystemet, som vi vil se neste gang.

- Oppgave 1

Å vite at Jupiters bane er 5.19 ganger større enn jorden, finn Jupiter -orbitalperioden.

Løsning

I henhold til definisjonen av astronomisk enhet er Jupiter fra Sun 5.19 UA, i henhold til Keplers tredje lov:

T²= r³= (5.19)³ år

Derfor T = (5.19)^3/2  år = 11.8 år

- Oppgave 2

Halley Comet besøker solen hver 75.3 år. Finne:

a) Den viktigste halvhjerting av bane.

b) Målet på apelium, hvis perihelium måler 0.568 Ua.

Løsning

Halley Comet besøker solen hver 75.3 år. Finne:

a) Den viktigste halvhjerting av bane.

b) Målet på apelium, hvis perihelium måler 0.568 Ua.

Løsning på

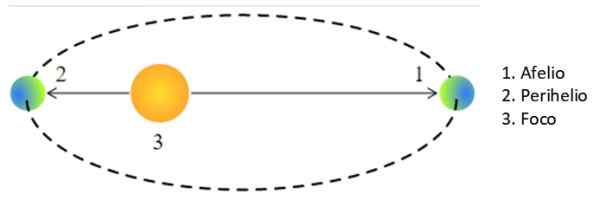
Når en planet eller noen annen stjerne er på sitt punkt nærmest solen, sies det at den er i perihelio, Og når det er videre, i Aphelion. I det spesielle tilfellet med en sirkulær bane, er R i Keplers tredje lov radius for bane.

Kan tjene deg: Antoinkonstanter: Formler, ligninger, eksempler

I den elliptiske bane er imidlertid den himmelske kroppen mer eller mindre borte fra solen, og er semi -major “A” gjennomsnittet mellom pålag og perihelium:

Figur 3. Aflio og Perihelio. Kilde: Wikimedia Commons. Pearson Scott Foresman / Public Domain

Derfor erstatter vi R med en i Keplers tredje lov, som resulterer for Halley i:

T²= a³→ A = (t)²³ → A = (75.3) ²³ UA = 17.832 Ua

Løsning b

A = ½ (perihelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 UA = 35.10 ua.

Eksperiment

Analysere bevegelsen av planetene krever uker, måneder og til og med år med nøye observasjon og registrering. Men i laboratoriet kan et veldig enkelt eksperiment utføres for å bevise at loven om Keplers likestillinger er oppfylt.

For dette kreves det et fysisk system der styrken som styrer bevegelsen er sentral, tilstrekkelig betingelse for at loven om områdene skal oppfylles. Et slikt system består av en masse knyttet til et langt tau, med den andre enden av den faste tråden til en støtte.

Deigen skiller en liten vinkel i likevektsposisjonen og skrives ut en liten impuls, slik at den utfører en oval (nesten elliptisk) bevegelse på det horisontale planet, som om det var en planet rundt solen.

På kurven beskrevet av pendelen, kan vi bevise at den feier like områder i like tider, ja:

-Vi vurderer vektorradioer som spenner fra attraksjonssenteret (innledende likevektspunkt) til massenes plassering.

-Og vi barmos mellom to øyeblikk på rad med lik varighet, i to forskjellige områder av bevegelsen.

Jo lengre pendeltråd og jo lavere vinkel som avviker fra vertikal.

Så nærmer de beskrevne ovale en ellipse, for eksempel den som planetene reiser.

Materialer

-Uutholdelig tråd

-1 deig eller metallkule malt hvit som fungerer som pendellinsen

-Hersker

-Transportør

-Bildekamera med automatisk strobe disk

-Støtter

-To kilder til belysning

-Et ark eller svart papp

Det kan tjene deg: stor knasteori: historie, prinsipper, data for og mot

Fremgangsmåte

Figursamlingen er nødvendig for å ta bilder av flere blinker av pendelen når banen følger. For å gjøre dette må du legge kameraet rett over pendelen og det automatiske strobe -albumet foran linsen.

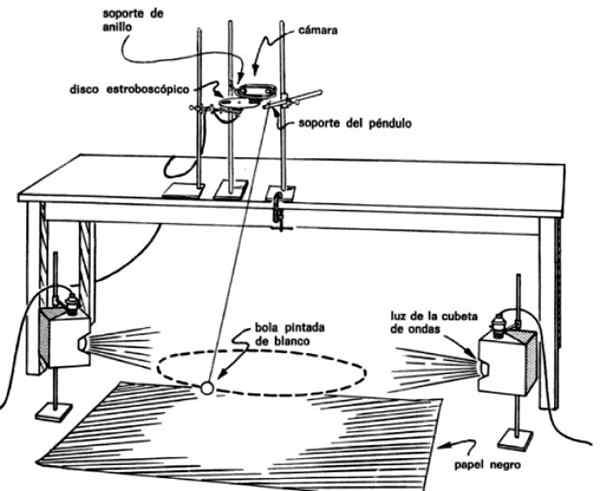Figur 4. Pendelmontering for å bekrefte at den feier like områder i like tider. Kilde: PSSC Laboratory Guide.

På denne måten oppnås bilder med regelmessige tidsintervaller av pendelen, for eksempel hver 0.1 eller hver 0.2 sekunder, som gjør det mulig å vite tiden det tok å flytte fra det ene punktet til det andre.

Du må også belyse massen til pendelen praktisk, sette lysene på begge sider. Linsen må males hvitt for å forbedre kontrasten på bakgrunnen, som består av et utvidet svart papir på bakken.

Nå må du sjekke at pendelen feier like områder i like tider. For dette er det valgt et tidsintervall, og punktene okkupert av pendelen i nevnte intervall er merket på papir.

På bildet er en linje trukket fra midten av det ovale til disse punktene, og derfor vil vi ha det første av områdene feid av pendelen, som er omtrent en elliptisk sektor som den som er vist nedenfor:

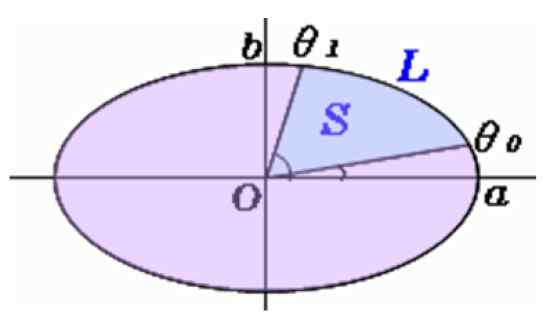Figur 5. Område av en elliptisk sektor. Kilde: f. Zapata.

Beregning av det elliptiske seksjonsområdet

Vinklene måles med transportøren θ_enten og θ₁, Og denne formelen brukes til å finne S, området i den elliptiske sektoren:

S = f (θ₁) - f (θ_enten)

Med F (θ) gitt av:

Noter det til og b De er henholdsvis semi -senijes større og mindre. Leseren skal bare bry seg om å måle semi -messen og vinklene nøye, siden det er online kalkulatorer for å enkelt evaluere dette uttrykket.

Imidlertid, hvis du insisterer på å foreta beregningen for hånd, må du huske at vinkelen θ måles i grader, men på tidspunktet for å legge inn dataene til kalkulatoren, må verdiene uttrykkes i radianer.

Da må du markere et annet par punkter der pendelen har investert samme tidsintervall, og tegne det tilsvarende området, og beregne verdien med samme prosedyre.

Verifisering av loven om like områder

Endelig gjenstår det å bekrefte at loven om områdene er oppfylt, det vil si at i like tider er like områder sveip.

Avviker resultatene litt fra det som forventet? Du må huske på at alle tiltak er ledsaget av deres respektive eksperimentelle feil.

Referanser

1. Keisan online kalkulator. Område av en elliptisk sektor kalkulator. Gjenopprettet fra: Keisan.Casio.com.
2. Opentax. Keplers lov om planetarisk bevegelse. Hentet fra: OpenStax.org.
3. PSSC. Laboratoriefysikk. Redaksjon tilbake. Gjenopprettet fra: Bøker.Google.co.
4. Palen, s. 2002. Astronomi. Schaum -serien. McGraw Hill.
5. Pérez r. Enkelt system med sentral kraft. Gjenopprettet fra: Francesphysics.Blogspot.com
6. Stern, d. De tre Kepler -lovene i planetarbevegelsen. Gjenopprettet fra: phy6.org.