Kirchhoff lov

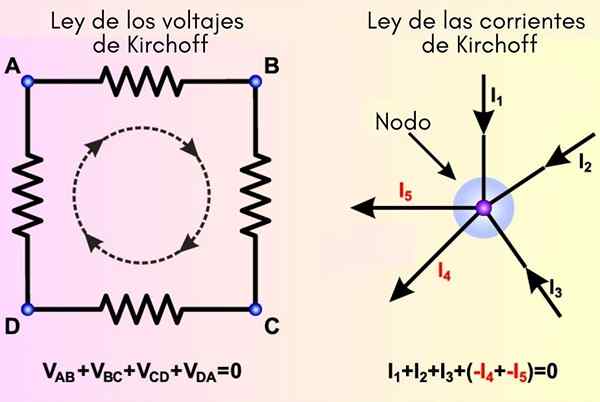
Kirchoffs lover stammer fra henholdsvis prinsippene om energi og belastningsbevaring. Til venstre er loven om masken etablert og til høyre strømmen

Hva er Kirchoffs lover?

De Kirchoff lov De består av å anvende prinsippet om bevaring av den elektriske ladningen og prinsippet om bevaring av energi på elektriske kretsløp, for å løse de som har flere masker.

Disse reglene, siden de ikke er lover i streng forstand, skyldes den tyske fysikeren Gustav Kirchoff (1824-1887). Bruken er viktig når Ohms lov ikke er nok til å bestemme spenninger og strømmer i kretsen.

Før uttalelsen og anvendelsen av Kirchoffs lover, er det praktisk å huske betydningen av noen viktige konsepter på elektriske kretsløp:

• Node: Unionspunkt mellom to eller flere ledende ledninger.
• Gren: Elementer i kretsen som er mellom to påfølgende noder, som den samme strømmen sirkulerer.
• Mesh: bane eller lukket sløyfe sammensatt av to eller flere grener, og som blir reist i samme retning, uten å gå gjennom samme punkt.

Kirchoffs første lov

Det er også kjent som loven om strømmer eller regel om noder, og fastslår det:

Summen av strømningene som kommer inn i en node er lik summen av strømningene som kommer ut av den.

Så på en matematisk måte uttrykkes den første loven som:

∑ i = 0

Der symbolet σ indikerer en sum.

Den forrige ligningen slår fast at ettersom den elektriske ladningen ikke er opprettet eller ødelagt, må hele strømmen (belastning per tidsenhet) som kommer inn i noden være lik den som kommer ut av den.

Kan tjene deg: kunstige satellitter

Eksempel

For å bruke lovens lovpris, tildeles et tegn på innkommende strømninger, og det motsatte tegnet på de utgående strømningene. Valget er helt vilkårlig.

Følgende bilde viser to strømmer som kommer inn i en node, tegnet med rødt: i₁ og jeg₂, og at når de forlater blir de vist i grønt: strømningene i₃, Yo₄ og jeg₅.

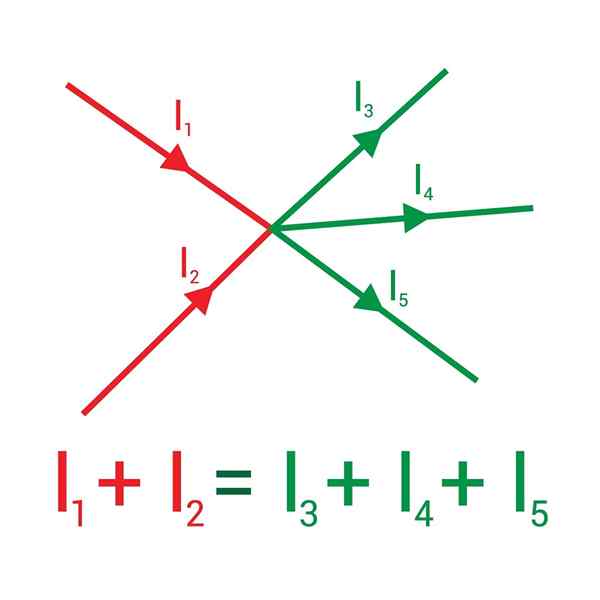Summen av strømningene som kommer inn i en node er lik summen av strømningene som kommer ut av den

Tilordne tegnet (+) til de innkommende strømningene, og (-) til den utgående, den første regelen til Kirchoff fastslår at:

Yo₁ + Yo₂ - Yo₃ - Yo₄ - Yo₅= 0 ⇒ i₁ + Yo₂ = Jeg₃ + Yo₄ + Yo₅

Kirchoffs andre lov

Andre navn på Kirchoffs andre lov er: Spenningsloven, Spenningsloven enten Mesh Law. I alle fall slår den fast at:

Den algebraiske summen av spenning synker langs et nett er lik 0.

Dette er en måte å bruke bevaring av energi i kretsen, siden spenningen i hvert element er endring av energi per lastenhet.

Derfor, når du reiser en lukket del (et nett), øker den algebraiske summen av spenningen og faller 0 og kan skrives:

∑ V = 0

Eksempel

I den følgende figuren har du nettet ABCDA, som en strøm sirkulerer i retning av klokken nåler og ruten kan starte når som helst i kretsen.

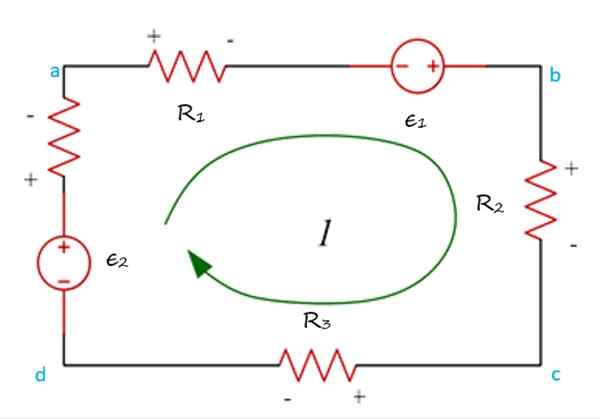Eksempel på et netting turnert i en tidsplan, der økninger og potensielle fall vises til å anvende Kirchoff -spenningsloven. Kilde: f. Zapata.

Det er også nødvendig. Det vanlige er å tilordne så positiv spenningsstigningen, det vil si når strømmen sirkulerer fra ( -) til (+). Deretter er spenningsfallet, som oppstår når strømmen går fra (+) til ( -), negativ.

Kan tjene deg: silisiumoksyd (SiO2): struktur, egenskaper, bruk, skaffelse

Å starte nettruten på punktet "A", er motstanden r₁. I den opplever belastningene en potensiell dråpe, symbolisert av skiltene (+) til venstre og ( -) over motstanden.

Derfor spenningen eller spenningen i r₁ Det har et negativt tegn.

Så når du en direkte spenningskilde, kalt ε₁, hvis polaritet er mindre (-) Mer (+). Der går de elektriske ladningene gjennom en potensiell økning, og denne kilden anses som positiv.

Etter denne prosedyren for den gjenværende motstanden og den andre kilden, oppnås følgende ligning som et resultat:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Hvor v₁, V₂ og v₃ er spenninger i motstand r₁, R₂ og r₃. Disse spenningene finner du fra Ohms lov: v = i · r.

Trening løst

Finn verdien av strømmer i₁, Yo₂ og jeg₃ vist på figuren.

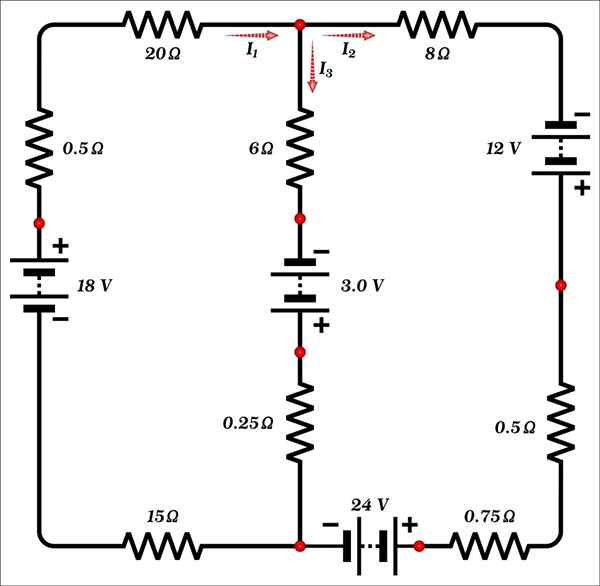
Løsning

Denne kretsen består bare av to masker og har 3 ukjente: strømningene og₁, Yo₂ og jeg₃, Så det kreves minst 3 ligninger for å finne løsningen.

I noden (punkt merket med rødt) som er øverst i kretsen på den sentrale grenen, observeres det at strømmen i₁ er innkommende, mens strømmer jeg₂ og jeg₃ De er utgående.

Derfor fører Kirchoff -strømloven til den første ligningen:

1) i₁ - Jeg₂ - Jeg₃ = 0

Den nedre noden gir samme informasjon, derfor er neste trinn å reise masker.

Første nett

For å etablere følgende ligning blir nettet til venstre reist i en plan, fra øverste venstre hjørne. Dette er den betydningen av at strømmer og strømmer sirkulerer₁ og jeg₃.

Kan tjene deg: optisk komparator: hva er det for og deler

Noter det:

• Yo₁ passerer gjennom motstandene på 20 Ω, 15 Ω og 0.5 Ω og 18 V -batteriet, hvor han opplever en potensiell økning.
• For sin del, jeg₃ Det krysser motstandene til den sentrale grenen på 6 Ω og 0.15 Ω og på 3 batteriet.0 V er en potensiell økning.

På samme måte brukes Ohm V = i ∙ R -loven for å etablere spenningen i hver motstand, i henhold til dette:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Bestiller vilkårene:

(−20 −15 - 0.5) ∙ Jeg₁ - (6 + 0.25) ∙ Jeg₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Andre netting

Den tredje ligningen oppnås ved å turnere nettet til høyre, og starte i noden på toppen av kretsen. Det observeres at:

• Yo₂ Gå gjennom motstandene på 8 Ω, 0.5 Ω og 0.75 Ω, pluss 12 V og 24 V -batterier. I henhold til polariteten til batteriene, er det i ruten en økning i potensialet i 12 V og reduseres i 24 V.
• Viktig: Turen for det andre nettet (i en plan) er imot i₃, Derfor spenningene i motstandene til 6 Ω og 0.25 Ω er potensielle stiger og bærer et positivt tegn. I henhold til polariteten til batteriene er det en økning i 12 V og fall i de på 24 V og 3 V.

Med alt dette når du:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Gjeldende beregning

Ligninger 1), 2) og 3) danner et system med 3 lineære ligninger med 3 ukjente, hvis løsning er:

Yo₁ = 0.381 a; Yo₂ = -0.814 a; Yo₃ = 1.195 a

Det negative tegnet i nåværende i₂ betyr at det flyter i motsatt retning av ordningen.