Relativ bevegelse i en dimensjon, i to dimensjoner, øvelser

Han relativ bevegelse av en partikkel eller et objekt er den som er observert med hensyn til et bestemt referansepunkt som observatøren har valgt, som kan være fikset eller flytting. Hastighet refererer alltid til et eller annet koordinatsystem som brukes til å beskrive det.

For eksempel er co -piloten av en bil i bevegelse og som reiser komfortabelt i setet i ro med hensyn til sjåføren, men han er ikke for en observatør som står på fortauet som ser bilen passere.

Figur 1. Fly opprettholder en viss relativ hastighet mellom dem når du praktiserer akrobatikk. Kilde: Pixabay.

Da er bevegelsen alltid relativ, men det hender at koordinat- eller referansesystemet vanligvis er valgt, og har sin opprinnelse i jorden eller bakken, et sted som anses som stasjonært. På denne måten fokuserer bekymringen på å beskrive bevegelsen av objektet som studeres.

Er det mulig å beskrive hastigheten på den sovende co -driveren med hensyn til en passasjer som reiser i en annen bil? Svaret er ja. Det er frihet til å velge verdien av (x_enten, og_enten, z_enten): Opprinnelsen til referansesystemet. Utvalget er vilkårlig og avhenger av observatørens preferanse, så vel som den enkle du gir for løsningen av problemet.

[TOC]

Relativ bevegelse i en dimensjon

Når bevegelsen går langs en rett linje, har mobiler hastigheter i samme retning eller i motsatt retning, begge sett av en observatør som står på land (T). Flytter observatøren når det gjelder mobiler? Ja, med samme hastighet bærer de, men i motsatt retning.

Hvordan beveger en mobil med hensyn til den andre? For å finne ut hastighetene er lagt til vektor.

Det kan tjene deg: Pluto (dvergplaneten)

-Løst eksempel 1

I referanse til figuren som er vist, angir den relative hastigheten på bilen 1 med hensyn til bilen 2 i hver situasjon.

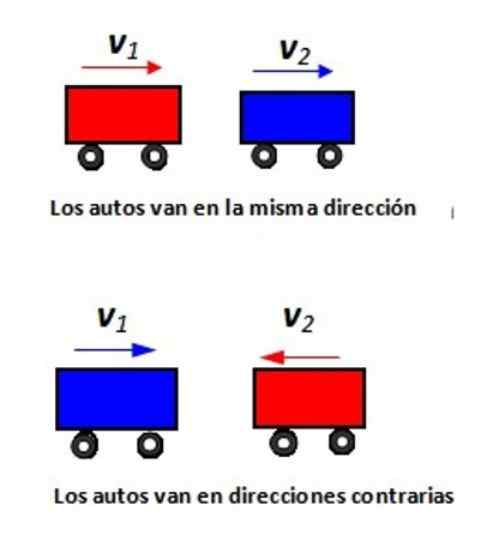Figur 2. To biler går på en rettlinjet vei: a) i samme retning og b) i motsatte retninger.

Løsning

Vi vil tildele positivt tegn til hastighetene til høyre, og negativt tegn til venstre. Hvis en mobil går til høyre ved 80 km/t, ser en passasjer i denne mobilen observatøren på bakken flytter til - 80 km/t.

Anta at alt skjer langs x -aksen. I den følgende figuren beveger den røde bilen seg på +100 km/t (sett fra T) og forbereder seg på å passere den blå bilen som beveger seg på +80 km/t (også sett fra T). Med hvilken hastighet ser du en passasjer nærme seg den røde bilen i den blå bilen?

Etikettene er: v _1/2 Auto 1 hastighet med hensyn til 2, v_1/t bilhastighet med hensyn til t, v_T/2 Tabellhastighet med hensyn til 2. Legge til vektorialt:

v_1/2 = v_1/t + v_T/2 = (+100 km/t - 80 km/t) x= 20 km/t x

Vi kan klare oss uten vektornotasjonen. Legg merke til abonnementene: Multipliser begge til høyre må skaffe den til venstre.

Og når de er i motsatt retning? Nå v_1/t = + 80 km/t og v_2/t = -100 km/t, derfor v_T/2 = + 100 km/t. Passasjeren til bilblå vil se den røde bilen nærme seg:

v_{1/2 =} v_1/t + v_T/2 = +80 km/t +100 km/t = 180 km/t

Relativ bevegelse i to og tre dimensjoner

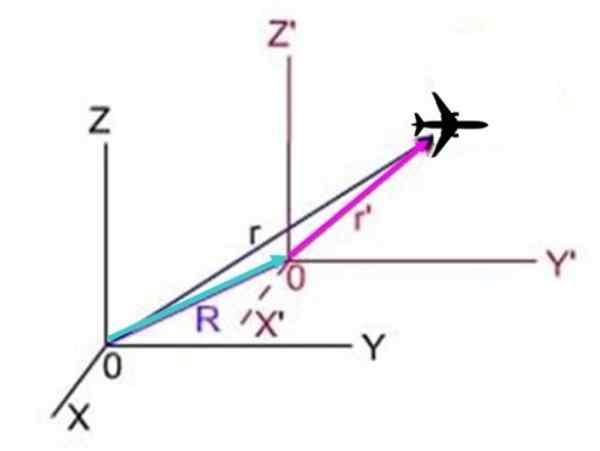
I følgende ordning, r Det er plasseringen av flyet sett fra systemet X og z, r'Det er stillingen fra systemet X og Z ' og R Det er systemets plassering med en premie med hensyn til systemet uten premie. De tre vektorene danner en trekant der R + r'= r, derfor r'= r - r.

Figur 3.- Flyet beveger seg med hensyn til to koordinatsystemer, i sin tur flytter det en av systemene med hensyn til det andre.

Siden derivatet med hensyn til stillingen er nettopp hastigheten, er resultatene:

Kan tjene deg: Parabolsk skudd: Kjennetegn, formler og ligninger, eksempler

v'= v - eller

I denne ligningen v'Det er flyets hastighet med hensyn til systemet X og Z ', v er hastigheten med hensyn til systemet X og z og eller Det er den konstante hastigheten på det viktigste systemet med hensyn til systemet uten premier.

-Trening løst 2 

Et fly er i nord retning med en hastighet med hensyn til luften på 240 km/t. Plutselig begynner det å blåse vind fra vest til øst med en hastighet på 120 km/ i henhold til jorden.

Finn: a) Flyets hastighet med hensyn til jorden, b) Avviket som piloten C) har utført korreksjonen som piloten må gjøre for å kunne peke direkte mot nord og den nye hastigheten med hensyn til land, en gang Korreksjonen er gjort.

Løsning

a) Følgende elementer er hatt: plan (a), jord (t) og vind (v).

I koordinatsystemet der nord er + og og den vest-østlige retningen er + x er det de gitte hastighetene og deres respektive etikett (abonnement):

v _Av = 240 km/t (+og); v _V/t = 120 km/t (+x); v _På = ?

Tilstrekkelige vektorsum er:

v _På = v _Av + v _V/t = 240 km/t (+og) + 120 km/t (+x)

Størrelsen på denne vektoren er: v _På = (240 ²+ 120²)^1/2 km/t = 268.3 km/t

b) θ = arctg (v _Av / v _V/t) = ARCTG (240/120) = 63.4. nord for øst eller 26.6. nordøst.

c) For å fortsette mot nord med denne vinden, må du peke flyets bue mot nordvest, slik at vinden skyver den direkte mot nord. I dette tilfellet vil hastigheten på flyet sett fra bakken være i +, og mens hastigheten på flyet med hensyn til vinden vil være nordvest (det er ikke nødvendigvis 26.6.).

Kan tjene deg: Bernoulli teorem

Av Pythagoras teorem:

v _På = (240 ²- 120²)^1/2 km/h = 207.8 km/t

α = arctg (v _V/t / v _På ) = ARCTG (120/207.8) = 30. nordvest

-Trening løst 3

En person tar 2 minutter å gå nedover en immobil mekanisk trapp. Hvis trappen fungerer, tar personen 1 minutt å gå nedover å være stille. Hvor lang tid tar personen å gå og med trappen som løper?

Løsning

Det er tre elementer å vurdere: personen (p), trappen (e) og bakken (e), hvis relative hastigheter er:

v_P/e : hastigheten til personen med hensyn til stigen; v_ER: trappens hastighet med hensyn til bakken; v_P/s: Personens hastighet med hensyn til bakken.

Som det sees fra bakken av en fast observatør, har personen som senker trappen (e) en hastighet v _P/s gitt av:

v _P/s = v_P/e + v_ER

Den positive sansen går ned trappene. Være t  tiden det tar å gå og gå og L avstand. Størrelsen på personen V _P/s er:

v_P/s = L / t

t₁ Det er tiden det tar å gå ned og gå med stoppet stigen: V _P/e = L / t₁

Og T₂ Den som tar deg fortsatt ned på trappen i bevegelse: V _ER = L / t₂

Kombinere uttrykk:

L / t = l / t₁ + L / t₂

Erstatte numeriske verdier og rydding t:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Deretter t = 1/1.5 minutter = 40 sekunder.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 84-88.
2. Figueroa, d. Fysisk serie for vitenskap og ingeniørfag. Volum 3. Utgave. Kinematikk. 199-232.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th. Ed. Prentice Hall. 62-64.
4. Relativ bevegelse. Gjenopprettet fra: kurs.Lumenarning.com
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 166-168.