Gjennomsnittlig definisjon av vinkelhastighet og formler, løste øvelser

De Gjennomsnittlig vinkelhastighet av rotasjon er definert som vinkelen rotert av vektortidsenhetens stilling til et punkt som beskriver sirkulær bevegelse. Bladene til en takvifte (for eksempel den som er vist i figur 1), følg sirkulær bevegelse og dens gjennomsnittlige vinkelhastighet beregnes ved å ta forholdet mellom den vendte vinkelen og tiden der den vinkelen ble reist.

Reglene etterfulgt av rotasjonsbevegelsen er på en viss måte lik de allerede pårørende til translasjonsbevegelsen. Avstandene som tilbakelagte kan også måles i meter, men vinkelstørrelsene tar på seg spesiell relevans fordi de letter beskrivelsen av bevegelsen i stor grad.

Figur 1. Viftebladene har vinkelhastighet. Kilde: Pixabay

Greske bokstaver brukes vanligvis til vinkelstørrelser og latinske bokstaver for tilsvarende lineære størrelser.

[TOC]

Definisjon og formler

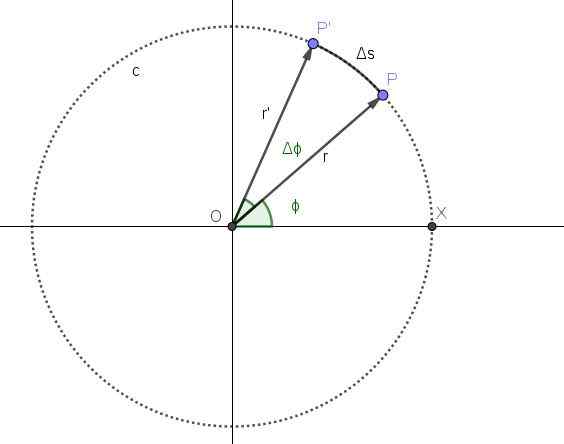
Figur 2 representerer bevegelsen av et punkt på en sirkulær bane C. Posisjonen P for punktet tilsvarer den øyeblikkelige T og vinkelposisjonen som tilsvarer det øyeblikket er ϕ. 

Fra det øyeblikket en periode er forløpt Δt. I den perioden er punktets nye stilling p 'og vinkelposisjonen har økt en vinkel Δϕ.

Figur 2. Sirkulær bevegelse av et punkt. Kilde: Selvlaget

Gjennomsnittlig vinkelhastighet ω er vinkelen som er reist per tidsenhet, slik at kvotienten Δϕ/ΔT vil representere den gjennomsnittlige vinkelhastigheten mellom øyeblikkene T og T+ΔT:

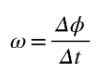
Ettersom vinkelen måles i radianer og tid på sekunder, er enheten til den gjennomsnittlige vinkelhastigheten rad/s. Hvis du vil beregne vinkelhastighet Akkurat på det tidspunktet T, må kvotienten Δϕ/Δt beregnes når Δt ➡0.

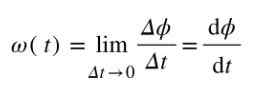Enheten for måling av øyeblikkelig vinkelhastighet er også rad/s.

Kan tjene deg: de 31 typene kraft i fysikk og deres egenskaper

Ensartet rotasjon

En rotasjonsbevegelse er ensartet hvis den til enhver tid observeres, er vinkelen den samme i samme tidsperiode. Hvis rotasjonen er ensartet, sammenfaller den vinkelhastigheten når som helst med den gjennomsnittlige vinkelhastigheten.

I en enhetlig rotasjonsbevegelse kalles tiden hvor en fullstendig sving kalles periode Og det er betegnet med t. 

I tillegg, når vinkelen er full, er den 2π, så i en jevn rotasjon er vinkelhastigheten ω relatert til t -perioden, med følgende formel:

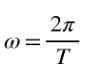
De Frekvens F av en enhetlig rotasjon som forholdet mellom antall svinger og tiden du bruker på å reise dem, det vil si at i tiden Δt er det da frekvensen vil være:

F = n/Δt

Som en omgang (n = 1) blir det reist i en tid t (perioden), er følgende forhold tilgjengelig:

F = 1/t

Det vil si i en enhetlig rotasjon er vinkelhastigheten relatert til frekvensen gjennom forholdet:

Ω = 2π ・ f

Forholdet mellom vinkelhastighet og lineær hastighet

Lineær hastighet v, Det er kvotienten mellom avstanden og tidsperioden som brukes til å reise den. I figur 2 er avstanden som er tilbakelagt lengden på buen Δs. 

Buen ΔS er proporsjonal med den reiste vinkelen Δϕ og radio R, og oppfyller følgende forhold:

ΔS = R ・ Δϕ

Når Δϕ måles i radianer.

Hvis vi deler det forrige uttrykket mellom tidsperioden ΔT, vil vi få:

(ΔS/Δt) = r ・ (Δϕ/Δt)

Det første medlemsforholdet er den lineære hastigheten og kvotienten til det andre medlemmet den gjennomsnittlige vinkelhastigheten:

Kan tjene deg: Mount Olympus (Mars)

v = r ・ ω

Løste øvelser

-Oppgave 1

Tipsene til takviftebladene vist i figur 1 beveger seg med en hastighet på 5 m/s og bladene er 40 cm radius.

Med disse dataene beregner: i) den gjennomsnittlige vinkelhastigheten på hjulet, ii) antall svinger som hjulet gir i et sekund, iii) perioden på sekunder.

Løsning 

i) Den lineære hastigheten er v = 5 m/s.

Radioen er r = 0,40 m.

Fra forholdet mellom lineær hastighet og vinkelhastighet fjerner vi sistnevnte:

v = r ・ ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 Turn / s

iii) t = 1 / f = 1 / (2 sving / s) = 0,5 s per fang.

-Oppgave 2

En leketøys spasertur beveger seg på en 2m radius sirkulært spor. Ved 0s er vinkelposisjonen 0 rad, men etter en tid er den vinkelposisjonen

φ (t) = 2 ・ t .

Med disse dataene 

i) Beregn gjennomsnittlig vinkelhastighet i de følgende tidsintervallene [0s, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5s] og til slutt i perioden [0.0, 1.5s]. 

ii) Basert på resultatene fra del I) hva som kan sies om bevegelsen?

iii) Bestem den gjennomsnittlige lineære hastigheten i samme tidsperiode i seksjon I)

iv) Finn vinkelhastighet og lineær hastighet for ethvert øyeblikk.

Løsning 

i) Gjennomsnittlig vinkelhastighet er gitt av følgende formel:

Vi fortsetter med å beregne den reiste vinkelen og tidsperioden som går i hvert intervall.

Intervall 1: Δϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0s = 1.0 rad

                   Δt = 0.5s - 0.0s = 0.5s

Kan tjene deg: BTU (termisk enhet): ekvivalenser, bruksområder, eksempler

                   Ω = Δϕ/Δt = 1.0Rad/0.5s = 2.0 rad/s

Intervall 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5s = 1.0 rad

                   Δt = 1.0s - 0.5s = 0.5s

                   Ω = Δϕ/Δt = 1.0Rad/0.5s = 2.0 rad/s

Intervall 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0s = 1.0 rad

                   Δt = 1.5s - 1.0s = 0.5s

                   Ω = Δϕ/Δt = 1.0Rad/0.5s = 2.0 rad/s

Intervall 4: Δϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0s = 3.0 rad

                   Δt = 1.5s - 0.0s = 1.5s

                   Ω = Δϕ/Δt = 3.0Rad/1.5s = 2.0 rad/s

ii) Med tanke på de tidligere resultatene, der den gjennomsnittlige vinkelhastigheten ble beregnet i forskjellige tidsintervaller, oppnås det samme resultatet alltid. Det ser ut til å indikere at det er en ensartet sirkulær bevegelse. Imidlertid er disse resultatene ikke avgjørende.

Måten å sikre konklusjonen er å beregne den gjennomsnittlige vinkelhastigheten for et vilkårlig intervall [T, T -t)

                                     Δt = t ' - t

                                     Ω = Δϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Dette betyr at leketøyets spasertur har en konstant gjennomsnittlig vinkelhastighet på 2 rad/s i en hvilken som helst tidsperiode som er vurdert. Men du kan gå lenger hvis øyeblikkelig vinkelhastighet beregnes:

Dette tolkes som lekebilen til enhver tid har konstant vinkelhastighet = 2 rad/s.

Referanser

1. Giancoli, d. Fysikk. Prinsipper med applikasjoner. 6. utgave. Prentice Hall. 30-45.
2. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 117.
3. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 33-52.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Utgave. Mexico. Cengage Learning Editors. 32-55.
5. Wikipedia. Vinkelhastighet. Gjenopprettet fra: Wikipedia.com