Negative tall konsept, eksempler, operasjoner

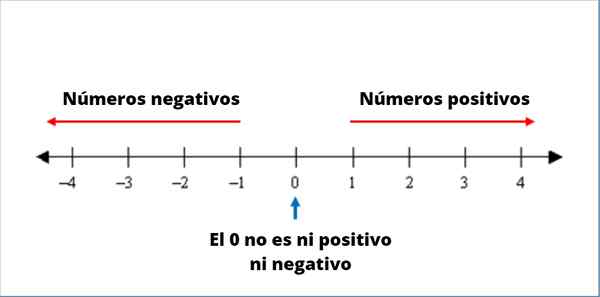
De Negative tall Det er de til venstre for den numeriske linjen, alltid foran et tegn -. Gjennom negativer er det mulig å representere mengder som er under eller til venstre for 0.

Disse tallene deltar aktivt i hverdagen: for eksempel hvis noen har en gjeld på $ 5, men de kan bare betale $ 3, skylder $ 2. Gjelden er betegnet med et negativt tegn for å skille den fra betalt sum.

Figur 1. Ordning med negative og positive tall

Posisjoner med lavt havnivå, temperaturer under frysepunktet til vannet og gulvene som er lavere enn gatenivået, kan betegnes med negative tall.

[TOC]

Hva er negative tall for?

Eksistensen av negativene utvider de mulige numeriske operasjonene. La oss sette eksemplet på subtraksjon av to tall. Hvis disse tallene tilhører de innfødte 1, 2, 3, 4, 5 ... er subtraksjonen bare fornuftig hvis det gjøres ved å trekke fra et annet nummer mindre enn ham.

Resultatet av operasjon 10 - 7 = 3 er rimelig, siden vi i prinsippet ikke kan ta bort ett beløp til enn det representerer.

Imidlertid, med negativene, vil denne andre situasjonen bli beskrevet godt: vi ønsker å kjøpe noe som er verdt $ 20, men vi har bare $ 15 og vi ba om $ 5 til en venn. Gjelden er, som vi har sagt, merket med et negativt tegn og dermed 15 - 20 = -5, som blir lest som "mindre 5".

Settet med negative hele tall knyttet til de innfødte og 0, utgjør det bredeste settet med hele tall z.

Men negativer kan også være brøk eller desimal og tilhører et enda bredere sett: det med reelle R -tall, som inkluderer rasjonelle og irrasjonelle.

Med alle av dem utføres kjente aritmetiske operasjoner, og tar seg av å operere etter enkle tegnregler som er forklart nedenfor.

Operasjoner med negative tall

Før du utfører operasjoner med negative tall, må du etablere noen enkle regler for å håndtere tegnet (-) som alltid må settes før og rekkefølgen på tall.

Kan tjene deg: Forskjell mellom en felles brøkdel og et desimaltall

Tenk på talllinjen vist på figuren, med negativene til venstre for 0 og de positive til høyre.

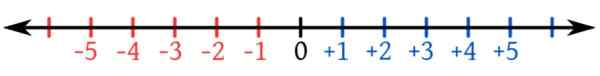Figur 2. Den numeriske linjen med negativene i rødt. Kilde: Wikimedia Commons.

Pilene til den numeriske linjen i begge retninger indikerer at det er uendelige tall. Observer også at det numeriske settet med heltall er et ordnet sett og ethvert negativt tall er mindre enn 0 og at ethvert positivt.

Dermed er -4 mindre enn 1, og -540 er for eksempel mindre enn 84.

Absolutt verdi

Avstanden mellom et hvilket som helst tall og 0 kalles absolutt verdi. Denne avstanden er alltid positiv og betegner av vertikale søyler, på denne måten:

│-5│ = 5

│+√6│ = √6

│-3/4│ = 3/4

│-10.2│ = 10.2

Det vil si den absolutte verdien av et hvilket som helst tall, enten det er positivt eller negativt, er det positive antallet av tallet. Dette konseptet vil tjene oss senere når vi opererer med negative tall.

Skilt

En annen veldig viktig detalj er skillet mellom tegnet på nummeret og tegnet på operasjonen.

Når et tall er positivt, er antallet på tallet vanligvis utelatt og det forstås at det uansett er positivt, men med negativene som ikke er mulig, er det derfor nødvendig å bruke parentes, la oss se:

-Riktig: 17 - (-6) eller også +17 - (-6)

-Feil: 17 - -6

-Feil: -5 + +7

-Riktig: - 5 + (+7) eller også -5 + 7

Når begrepene absolutt verdi, orden og viktigheten av det negative tegnet er klare, kan vi gå videre til elementære operasjoner.

Addisjon

Vi skiller følgende tilfeller, og starter med summen av to positiver, hvis prosedyre allerede er veldig kjent:

-Legg til to positive tall: ( + a) + ( + b) = a + b

Noe som betyr at vi legger til som vanlig, la oss se:

(+8) + (+5) = 8 + 5 = 13

-Legg til to negative tall: (-a) + (-b) =-(a + b)

I dette tilfellet legger vi til de absolutte verdiene av tallene og til resultatet blir et negativt tegn lagt før, som dette:

Kan tjene deg: typer integraler

(-7) + (-11) = - (7+ 11) = - 18

-Legg til et negativt og en positiv: ( + a) + (-b)

For denne operasjonen trekkes de absolutte verdiene, og resultatet bærer tegnet på tallet med den høyeste absolutte verdien. La oss gjøre noen tilfeller:

a) (-16) + (+3)

De respektive absolutte verdiene er 16 og 3, antallet med den høyeste absolutte verdien er 16, hvis tegn er negativt, da:

(-16) + (+3) = - (16 - 3) = -13

b) (+8) + (-3) = + (8-3) = +5 = 5

Summen av negativer er også kommutativ, noe som betyr at orden i annonsene ikke er viktig for resultatet.

De tidligere reglene gjelder hvis du vil legge til mer enn to tall, noe som kan gjøres med den assosiative egenskapen: a + b + c = (a + b) + c = a + (b + c).

Før du ser et eksempel i dette tilfellet, la oss se subtraksjon av to hele tall først.

Subtraksjon

Subtraksjonen er definert som summen av det motsatte. Det motsatte av et tall A er -A, som dette:

-4 er det motsatte av + 4

½ er det motsatte av -½

Hvis de ber oss om å utføre subtraksjon av to tall, uavhengig av skiltet, legger vi ganske enkelt det motsatte av det andre:

a) (-53) -(+8) = (-53)+( -8) = -(53+8) = -61

b) (+7) - (-12) = (+7)+(+12) = 7+12 = 19

c) (+2) - (+π) = (+2)+( - π) = 2 - π

Eksempel

Utfør følgende operasjon (+4) + (-7) + (+19)

Vi skriver det slik slik ved hjelp av firkantede parenteser for å indikere operasjonen som skal utføres først:

(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [-(4 -7)] + 19 = [-(-3)] + 19 = 19 - (-3) = 19 + (+3) = 22

Multiplikasjon

Skiltregelen for multiplikasjon er oppsummert i følgende figur:

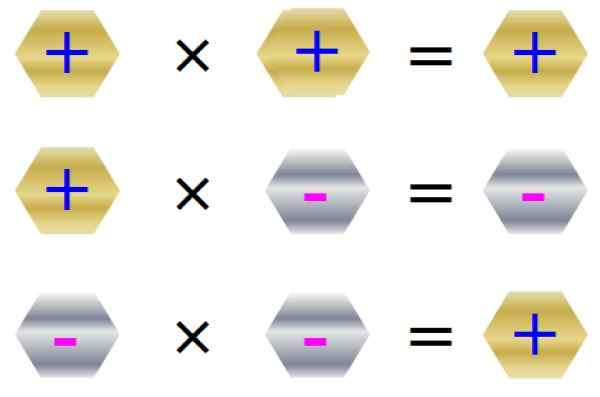Figur 3. Tegnregler for multiplikasjon. Kilde: f. Zapata.

Multiplikasjonsegenskaper

-Commutivity: Rekkefølgen på faktorene endrer ikke produktet, derfor ≠ = b.Hvor A og B er negative, hele eller brøkdemper.

Kan tjene deg: irrasjonelle tall: historie, egenskaper, klassifisering, eksempler

-Assosiativitet: La A, B og C hele tall, det er oppfylt det (a.b). C = a. (b.c)

-Distribusjon angående summen: La A, B og C hele tall, det er gyldig det. (b+c) = a.b +a.c

Eksempel

(-3/2) x [(-5) + (+4)-( + 2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6)/2 = 9/2

Operasjonen mellom firkantede parenteser kunne også ha blitt løst og resultatet multiplisert med (-3/2), som dette:

(-3/2) x [-5 + 4-2] = (-3/2) x (-3) = 9/2

Inndeling

Skiltregelen for divisjon er utsatt i følgende figur:

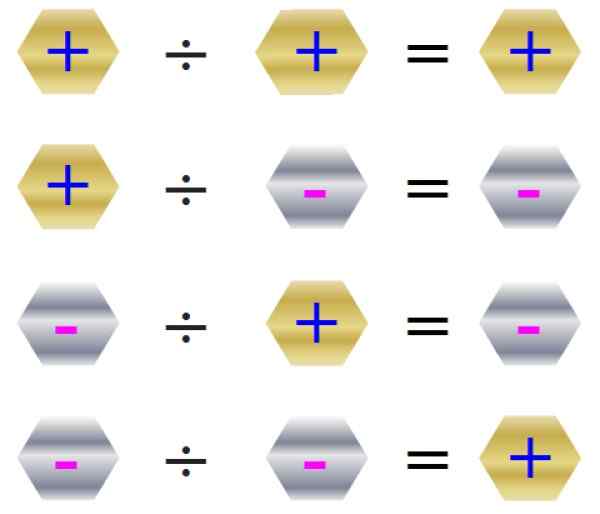Figur 4. Tegn regel for divisjon. Kilde: f. Zapata.

Divisjonen er ikke kommutativ og vanligvis ved ÷ b ≠ B ÷ A, ikke tillatt inndelingen mellom 0. La oss se på et eksempel:

(-54) ÷ (+3) = -18

For å oppnå dette resultatet er kvotienten ganske enkelt gjort, og tegnet er valgt i henhold til tabellen vist på figuren, som tilsvarer det tredje alternativet.

Potensering

Potensering er driften av skjemaet tilⁿ, Hvor er basen og n er eksponenten. Basen og eksponenten kan ha noe tegn.

-Hvis basen er negativ eller positiv og eksponenten er hel, er resultatet av operasjonen alltid positiv.

-Når basen er positiv og eksponenten er helt, er resultatet positivt.

-Og hvis basen er negativ og eksponenten er merkelig, er resultatet negativt.

Fraksjonelle eksponenter vil bli uttrykt vekselvis som rot, for eksempel en kvadratrot som tilsvarer den brøkeksponenten ½, en kubikkrot tilsvarer eksponenten 1/3 og så videre.

La oss se på noen eksempler:

a) (-3)³ = (-3) x (-3) x (-3) = -27

b) 16 ^-1/2 = 1 / √16 = ¼

c) (+8) ^1/3 = kubisk rot på 8 = 2

Referanser

1. Baldor, a. 1986. Aritmetikk. Codex -utgaver og distribusjoner.
2. Figuera, J. 2000. Matematikk 7. plass. Grad. Co-bo-utgaver.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Matematikk er morsomt. Hvordan legge til og trekke fra positiv og negative tall. Gjenopprettet fra: Mathisfun.com
5. Wikipedia. Negative tall. Gjenopprettet fra: er.Wikipedia.org.