Ortoedro -formler, område, volum, diagonal, eksempler

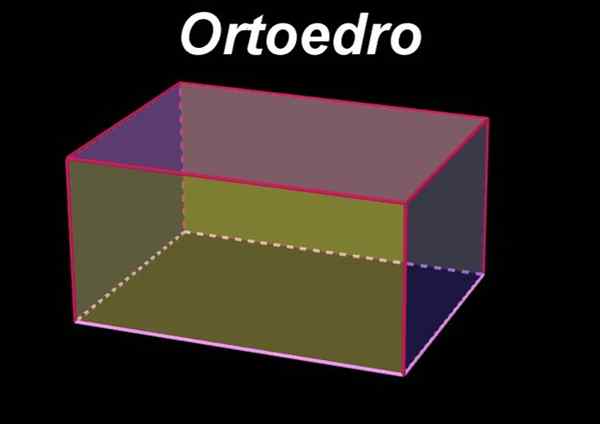
Han Orthoedro Det er en volumetrisk eller tre -dimensjonal geometrisk figur som er preget av å ha seks rektangulære ansikter, slik at motsatte ansikter er i parallelle plan og er identiske eller kongruente rektangler med hverandre. På den annen side er ansiktene ved siden av et gitt ansikt i plan vinkelrett på det i det første ansiktet.

Det kan også vurderes når Orthoedro som et ortogonalt rektangulært baseprisme, der Dihedros vinkler Dannet av de to -sidige planene ved siden av en felles kant, måler de 90º. Den dihedrale vinkelen mellom to ansikter måles i skjæringspunktet mellom ansikter med et vinkelrett og vanlig plan for dem.

Figur 1. Orthoedro. Kilde: f. Zapata med Geogebra.

På samme måte er ortoedroen en Rektangel parallellpiped, Siden dette er definert til parallellpiped som den volumetriske figuren på seks ansikter, som er parallelle to til to.

I ethvert parallellpiped er ansiktene parallellogrammer, men i rektangelet parallellpiped må ansiktene være rektangulære.

[TOC]

Deler av ortoedro

Delene av en polyhedron, for eksempel ortoedro, er:

-Kanter

-Hjørner 

-Ansikter

Vinkelen mellom to kanter av et ansikt av ortoedro sammenfaller med den dihedrale vinkelen dannet av de to andre ansiktene ved siden av hver av kantene, og danner rett vinkel. Følgende bilde tydeliggjør hvert konsept:

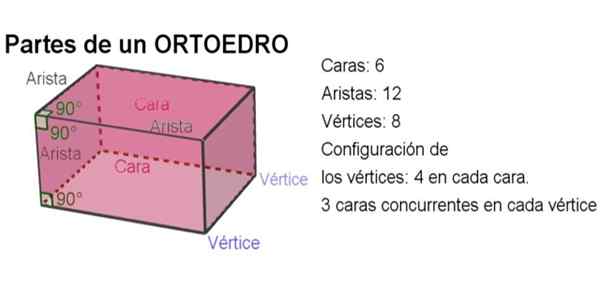Figur 2. Deler av en ortoedro. Kilde: f. Zapata med Geogebra.

-Totalt har en ortoedro 6 ansikter, 12 kanter og 8 hjørner.

-Vinkelen mellom to kanter er en rett vinkel.

-Den dihedrale vinkelen mellom to sider er også rett.

-I hvert ansikt er det fire hjørner, og i hvert toppunkt deltar tre gjensidig ortogonale ansikter.

Kan tjene deg: Hva er et Capicúa -nummer? Egenskaper og eksempler

Ortoedro -formler

Område

Overflaten eller området til en Orthoedro Det er summen av områdene i ansiktene deres.

Hvis de tre kantene som er enige i et toppunkt har tiltak A, B og C, som vist i figur 3, har forsiden et område et område C⋅B Og bakgrunnsansiktet har også et C⋅B -område.

Deretter har de to sidesiktene et område A⋅B Hver. Og til slutt har ansiktene på gulvet og taket område A⋅C Hver.

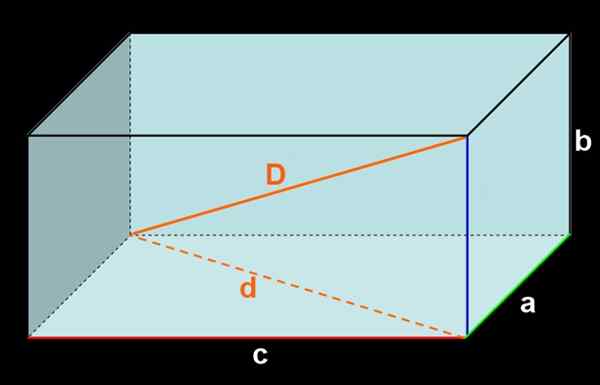Figur 3. Ortoedro av dimensjoner A, B, C. Intern diagonal d og ekstern diagonal d.

Å legge til området for alle ansikter oppnås:

A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a

Tegne vanlig faktor og bestille vilkårene:

A = 2⋅ (A⋅B + B⋅C + C⋅a)

Volum

Hvis Orthoedro antas som et prisme, beregnes volumet som følger:

Volum = prisme baseområde x høyden på prisme

I dette tilfellet blir dimensjonsgulvet tatt som en rektangulær c og til, Så basisområdet er C⋅a.

Høyden er gitt av lengden b Fra ortogonale kanter til sidene til og c.

Multiplisere basisområdet (A⋅C) etter høyde b Du har volumet V Fra Orthoedro:

V = A⋅B⋅C

Intern diagonal

I en ortoedro er det to typer diagonaler: eksterne diagonaler og interne diagonaler.

De ytre diagonalene er på rektangulære ansikter, mens de interne diagonalene er segmentene som blir sammen med to motsatte hjørner, og blir forstått av motsatte hjørner de som ikke deler noen kant.

I en ortoedro er det fire interne diagonaler, alle av like store mål. Lengden på de interne diagonalene kan oppnås ved å bruke Pythagoras -teoremet for rektangler.

Det kan tjene deg: trigonometriske funksjoner: grunnleggende, i det kartesiske planet, eksempler, trening

Lengden d av den ytre diagonalen til ortoedro -gulvet oppfyller det pytagoreiske forholdet:

d² = a² + c²

Tilsvarende den indre målingsdiagonalen til det pytagoreiske forholdet:

D² = d² + b².

Kombinere de to foregående uttrykkene du har:

D² = a² + c² + b².

Til slutt er lengden på noen av de interne diagonalene til ortoedro gitt av følgende formel:

D = √ (a² + b² + c² ). 

Eksempler

- Eksempel 1

En murer bygger en ortoedro -formet tank hvis indre dimensjoner er: 6 m x 4 m base og 2 m høy. Det blir bedt om:

a) Bestem den indre overflaten av tanken hvis den er helt åpen i den øvre delen. 

b) Beregn volumet på det indre rommet til tanken.

c) Finn lengden på en indre diagonal.

d) Hva er kapasiteten til tanken i liter?

Løsning på

Vi vil ta dimensjonene til den rektangulære basen a = 4 m og c = 6 m og høyden som b = 2 m

Området til en ortoedro med dimensjonene som er gitt er gitt av følgende forhold:

A = 2⋅ (A⋅B + B⋅C + C⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

Det er å si:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

Det forrige resultatet er området til ortoedroen lukket med de gitte dimensjonene, men siden det er en tank som er fullstendig oppdaget i den øvre delen, for å oppnå overflaten på innvendige vegger i tanken, området for det manglende lokket det er:

C⋅a = 6 m ⋅ 4 m = 24 m².

Til slutt vil den indre overflaten av tanken være: S = 88 m² - 24 m² = 64 m².

Løsning b

Det indre volumet av tanken er gitt av volumet av en ortoedro av de indre dimensjonene til tanken:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Løsning c

Den indre diagonalen til en oktaedron med dimensjonene til det indre av tanken har en lengde gitt av:

Kan tjene deg: kontinuerlig tilfeldig variabel

√ (a² + b² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Utføre de indikerte operasjonene vi har:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Løsning d

For å beregne tankkapasiteten i liter, er det nødvendig å vite at volumet av en kubikk -desimeter tilsvarer kapasiteten til en liter. Det hadde tidligere blitt beregnet i volum i kubikkmeter, men det må transformeres til kubikk desimeter og deretter til liter:

V = 48 m³ = 48 (10 DM)³ = 4.800 DM³ = 4.800 l

- Oppgave 2

Et glassakvarium har en kubikkform på 25 cm side. Bestem området i M², Volumet i liter og lengden på en indre diagonal i CM.

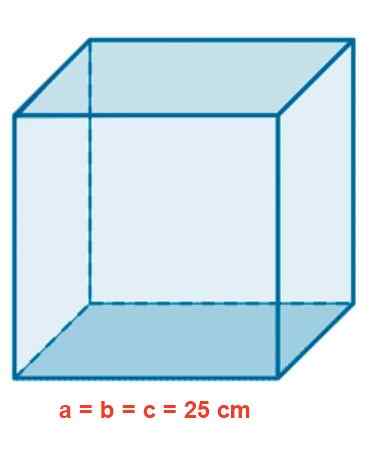Figur 4. Kubikkglass akvarium.

Løsning

Området beregnes av den samme ortoedro -formelen, men tar hensyn til at alle dimensjoner er identiske:

A = 2⋅ (3 a⋅a) = 6⋅ a² = 6⋅ (25 cm)² = 1.250 cm²

Kubens volum er gitt av:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 DM)³ = 15.625 DM³ = 15.625 l.

Lengden d av den indre diagonalen er:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Referanser

1. Arias j. Geogebra: Prism. Gjenopprettet fra: YouTube.com.
2. Beregning.DC. Øvelser og problemer løst i områder og volumer. Gjenopprettet fra: Beregning.DC.
3. Salvador r. Pyramid + Orthoedro med Geogebra (IHM). Gjenopprettet fra: YouTube.com
4. Weisstein, Eric. "Ortoedro". Mathworld. Wolfram Research.
5. Wikipedia. Orthoedro. Gjenopprettet fra: er.Wikipedia.com