Hva er tallene for? De 8 hovedbrukene

De Tall tjener For en uendelig oppgaver i verden. I de fleste prosesser er objekter og steder tallene involvert, selv om de ikke alltid er tydelige. Dets viktigste bruk er at de tillater å telle objekter.

Det er vanskeligere å finne situasjoner der tall ikke er involvert. Dette er en sentral del av mange hverdagssituasjoner i livet.

For eksempel rutene som planene bestemmes av jordens koordinater, som er dannet fra tall; Det samme gjelder blant annet skip og ubåter.

Hovedbruk av tall

1- Tell objekter

Siden barn er den første tingen å lære å gjøre med tall å telle objekter, som gir tilleggsinformasjon i forskjellige situasjoner.

I det følgende bildet er det for eksempel to grupper av epler.

Begge gruppene inneholder epler. Men når det sies at det i den ene gruppen er 3 epler, og i den andre gruppen er det 2 epler, blir en forskjell mellom gruppene nevnt, som er mengden epler i hver.

Dette kan gjøres å fortelle mengden epler, noe som er mulig takket være tallene.

2- Operasjoner algebraisk

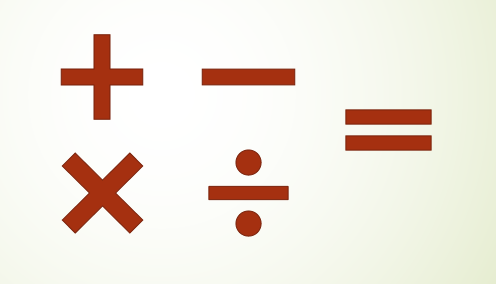
Etter å ha lært å telle, er følgende bruk av tallene som læres til barn relatert til algebraiske operasjoner, for eksempel sum, subtraksjon, multiplikasjon og inndeling.

Disse fire operasjonene brukes hver dag for en veldig stor mengde mennesker, og er en av de vanligste å legge til for å få prisen som skal betales i et supermarked.

3- representerer verdien av pengene

Før det var penger, gjorde folk utvekslinger eller byttehandel mellom gjenstander av deres tilhørighet.

Da ble pengene introdusert, noe som letter denne typen prosedyrer. Antallet som vises i hver billett eller valuta representerer verdien av det samme.

Så for å vite hvor mye verdi en billett har, trenger du bare å se nummeret den har; det vil si mengden av pengeenheter som den representerer.

4- Identifiser objekter

Tall hjelper også med å identifisere objekter. For eksempel vises to busser i følgende bilde.

Den eneste forskjellen de har er identifikasjonsplaten deres, som har tall.

Takket være tallene vil eieren av hver buss vite hvilken som er din. Det samme skjer for eksempel med identitetsdokumentene til folket.

5- Binære tall

En veldig vanlig, men ikke veldig tydelig bruk, er binære tall. Binære tall er representert ved bruk av bare nuller og noen.

For eksempel er nummer 16 i binære tall 10000 -nummeret.

Binære tall brukes i databehandlingsverdenen. Dataene som håndteres av datamaskiner internt er representert av nuller og noen, siden de jobber med to nivåer av spenninger.

Når en datamaskin ønsker å sende et faktum, er disse dataene representert med en binær kode der null representerer et spenningsnivå og en representerer det andre spenningsnivået.

6- mål

For å måle lengden på et objekt, brukes tallene i tillegg til måleenheten (meter, miles).

Det samme skjer når du vil vite vekten til et objekt eller lufttrykket som kan støtte sykkelgummi.

7- De representerer avstander

Tallene har tjent til å universalisere avstandene, enten det er i metriske lengder eller milene til Anglo -Saxon -systemet. Og i antikken hadde hver sivilisasjon sin egen måte å beregne avstandene, og var stort sett veldig unøyaktig og subjektiv.

Det er faktisk fortsatt mulig å finne mennesker som, når de spør hvor langt et sted er, å svare på "hva som tar en sigar", og gir en tid som en representasjon av avstanden og ikke av lengde. 

8- Bestill gatene

Tallene er den internasjonale måten å lokalisere hvert hus, bygning, lokal eller institusjon, siden det ligger på en gate og med et tall. 

For eksempel i Spania er gatene oppført av jevnaldrende og rare. Å være hjemmene til et fortau nummerert med jevnaldrende (2,4,6,8,10 ...) og de av det andre fortauet på samme gate med oddetall (1,3,5,7,9 ...). Dermed kan en person fra Madrid leve på Nicasio Gallego Street nr. 9.

Referanser

1. Barker, l. (2011). Levede tekster for matematikk: Antall og operasjoner. Lærer skapte materialer.
2. BURTON, m., Fransk, c., & Jones, t. (2011). Vi bruker tall. Benchmark Education Company.
3. Doudna, k. (2010). Ingen slumbers når vi bruker tall! ABDO Publishing Company.
4. Fernández, J. M. (nitten nittiseks). Chemical Bond tilnærmingsprosjekt. REVERTE.
5. Hernández, J. d. (s.F.). Matematikknotat. Terskel.
6. Lahora, m. C. (1992). Matematiske aktiviteter med barn fra 0 til 6 år. Narcea -utgaver.
7. Marín, e. (1991). Spansk grammatikk. Redaksjonell progreso.
8. Tocci, r. J., & Widmer, n. S. (2003). Digitale systemer: Prinsipper og applikasjoner. Pearson Education.