Parallellpiped

Parallelepipedene er seks -sidede geometriske figurer, der motsetninger er parallelle med hverandre. Eksempel: en murstein, en skoboks, en bøtte osv.

Hva er en parallellpiped?

EN parallellpiped Det er en geometrisk kropp dannet av seks ansikter, hvis hovedkarakteristikk er at alle ansiktene er parallellogrammer og også de motsatte ansiktene er parallelle med hverandre. Det er en vanlig polyhedron i hverdagen vår, siden vi kan finne den i skobokser, formen på en murstein, formen på en mikrobølgeovn, etc.

Å være en polyhedron, inneholder parallellpiped et begrenset volum og alle ansiktene er flate. Det er en del av gruppen av prismer, som er de polyedraene der alle dens toppunkter er inneholdt i to parallelle plan.

Elementer av parallellpiped

Ansikter

De er hvert av regionene dannet av parallellogrammer som begrenser parallellpiped. En parallellpiped har seks ansikter, der hvert ansikt har fire tilstøtende ansikter og et motsatt. I tillegg er hvert ansikt parallelt med det motsatte.

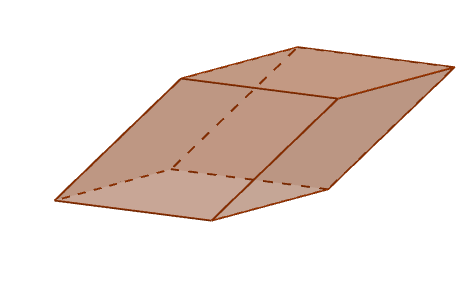Perspektiv på en parallellpiped

Kanter

De er den vanlige siden av to ansikter. Totalt har en parallellpiped tolv kanter.

Toppunkt

Det er det vanlige punktet med tre ansikter som ligger tilstøtende to til to. En parallellpiped har åtte hjørner.

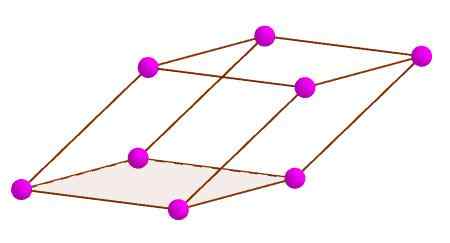Hjørner til en parallellpiped

Diagonal

Gitt to ansikter av en parallellpiped motsatt av hverandre, kan vi tegne et linjesegment som går fra toppunktet til det ene ansiktet til det motsatte toppunktet til det andre.

Dette segmentet er kjent som den parallellpipede diagonalen. Hver parallellpiped har fire diagonaler.

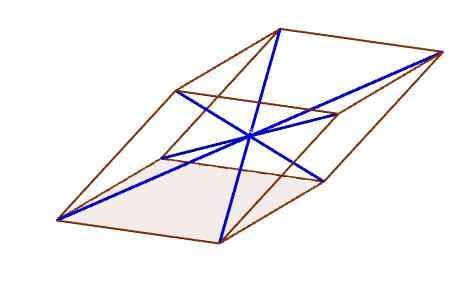Diagonaler av en parallellpiped

Senter

Det er punktet der alle diagonaler krysser hverandre.

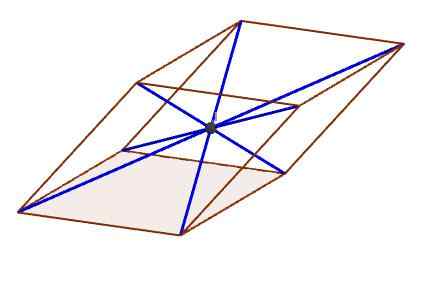Poenget i figuren indikerer sentrum, der alle diagonaler krysser hverandre

Kjennetegn på parallellpiped

Som vi allerede nevnte, har denne geometriske kroppen tolv kanter, seks ansikter og åtte hjørner.

I en parallellpiped kan tre sett dannet av fire kanter identifiseres, som er parallelle med hverandre. I tillegg overholder kantene på disse settene også egenskapen til å ha samme lengde.

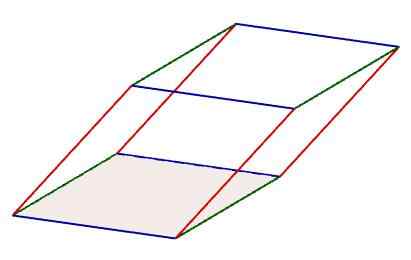Kjennetegn på parallellpiped

En annen eiendom som ble posert.

I tillegg er parallellpipedene, som er konvekse polyhedros, overholder Eulers teorem for polyhedros, noe som gir oss et forhold mellom antall ansikter, antall kanter og antall hjørner. Dette forholdet er gitt i form av følgende ligning:

C + V = A + 2

Denne funksjonen er kjent som Eulers karakteristikk. Hvor C er antall ansikter, og antall hjørner og antall kanter.

Typer paralleepípedos

Vi kan klassifisere parallellepípedos basert på ansiktene deres, på følgende typer:

Orthoedro

De er parallellepípedosene der ansiktene deres består av seks rektangler. Hvert rektangel er vinkelrett på de som det deler kant. De er de vanligste i hverdagen vår, dette er den vanlige formen for sko og murbokser.

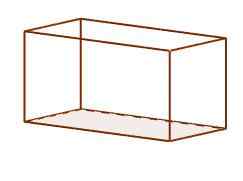Orthoedro parallellpiped

Vanlig kube eller heksaedro

Dette er et spesielt tilfelle av den forrige, der hvert av ansiktene er et firkant.

Kan tjene deg: ellipseVanlig kube eller heksaedro

Kuben er også en del av de geometriske kroppene som kalles platoniske faste stoffer. Et platonisk faststoff er en konveks polyhedron, slik at både dens ansikter og dens indre vinkler er lik hverandre.

Romboedro

Det er en parallellpiped som har en rhombus. Disse rhombuses er alle lik hverandre, siden de deler kanter.

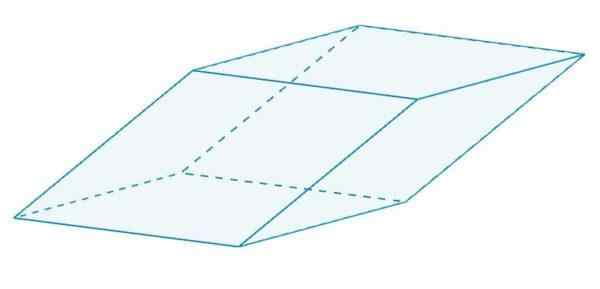En Romboedro

Romboiedro

Hans seks ansikter er rhomboid. Husk at en rhomboid er en firesidig polygon og fire vinkler som er lik to til to. Rhomboidene er parallellogrammer som verken er firkantede eller rektangler eller rhombuses.

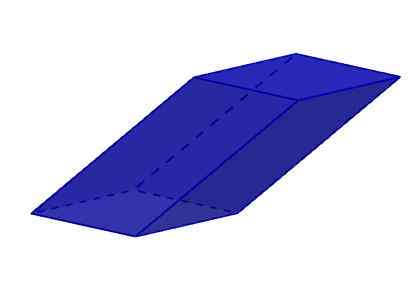Romboiedro

På den annen side er de skrå parallellepipedene de der minst en høyde ikke samsvarer med kanten. I denne klassifiseringen kan vi inkludere rhomboedros og rhomboiedros.

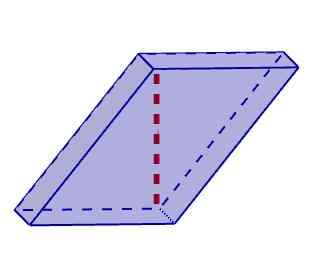Skrå parallellpiped

Diagonal beregning

For å beregne diagonalen til en ortoedro kan vi bruke Pythagoras teorem for r³.

Husk at en ortoedro har kjennetegn på at hver side er vinkelrett på sidene som deler kant. Fra dette faktum kan vi utlede at hver kant er vinkelrett på de som deler Vertex.

For å beregne lengden på en diagonal av en ortoedro fortsetter vi som følger:

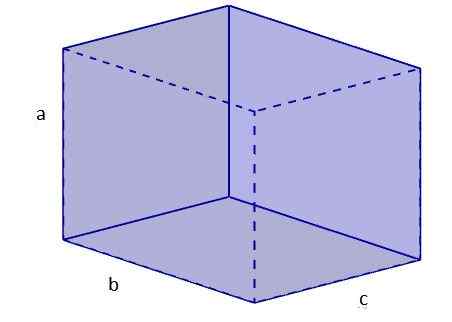
1. Vi beregner diagonalen til et av ansiktene, som vi vil sette med base. For dette bruker vi Pythagoras teorem. La oss navngi den diagonalen D_b.

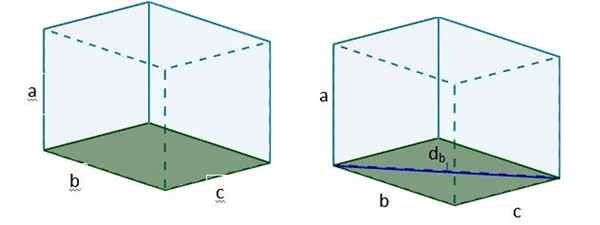
2. Deretter med d_b Vi kan danne en ny rektangel -trekant, slik at hypotenusen til nevnte trekant er den diagonale D søkt.

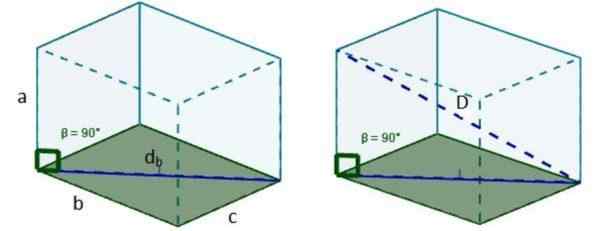
3. Vi bruker Pythagoras teorem igjen, og vi har at lengden på den diagonalen er:

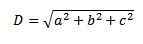
En annen måte å beregne diagonal på en mer grafisk måte er med summen av frie vektorer.

Husk at to frie vektorer A og B tilsettes ved å plassere halen til vektor B med spissen av vektoren a.

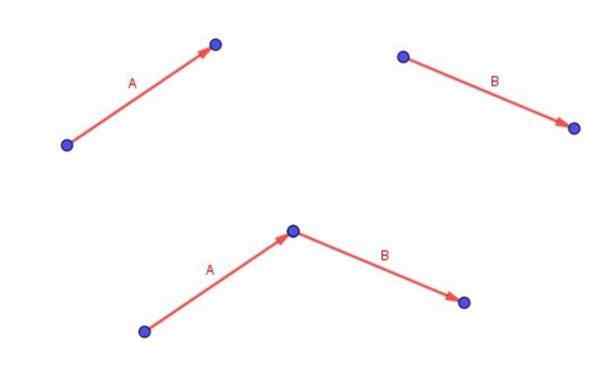
Vektoren (A + B) er den som begynner i halen til A og slutter på spissen av B.

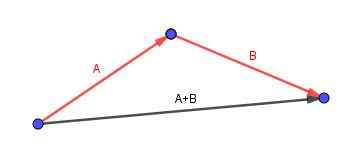
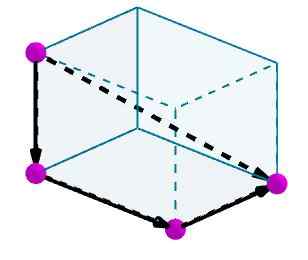
Tenk på en parallellpiped som vi ønsker å beregne en diagonal. Vi identifiserer kantene med praktiske orienterte vektorer.

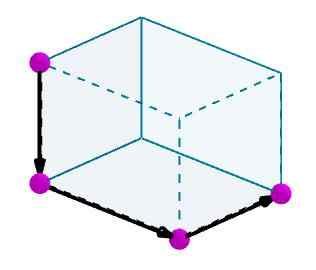
Så legger vi til disse vektorene, og den resulterende vektoren vil være diagonalen til parallellpiped.

Område av en parallellpiped

Området til en parallellpiped er gitt av summen av hvert av områdene i ansiktene.

Hvis vi bestemmer en av sidene som base,

TIL_L + 2_B = Totalt område

Hvor du skal_L Det er lik summen av områdene på alle sider ved siden av basen, kalt sideområdet og til_B Det er basisområdet.

Avhengig av hvilken type parallellpiped som vi jobber, kan vi omskrive nevnte formel.

Område av en ortoedro

Er gitt av formelen

A = 2 (AB + BC + CA).

Eksempel 1

Gitt følgende ortoedro, med sidene A = 6 cm, b = 8 cm og c = 10 cm, beregner det parallellpipede området og lengden på dets diagonal.

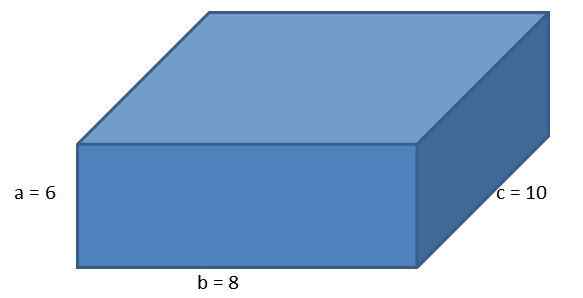
Bruke formelen for området til en ortoedro vi må

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Legg merke til at ettersom en ortoedro er lengden på noen av de fire diagonalene er den samme.

Det kan tjene deg: Ubestemt integral: egenskaper, applikasjoner, beregning (eksempler)

Bruke Pythagoras -teoremet for verdensrommet vi må

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Kubområde

Ettersom hver kant har samme lengde, har vi at A = B og A = C. Erstatte i forrige formel vi har

A = 2 (AA + AA + AA) = 2 (3A²) = 6a²

A = 6a²

Eksempel 2

Boksen til en spillkonsoll har formen som en kube. Hvis vi ønsker å pakke denne boksen med gavepapir, hvor mye papir vil vi bruke på å vite at lengden på kantene på kuben er 45 cm?

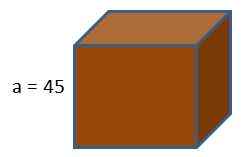
Ved å bruke formelen til kubeområdet får vi det

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Område av en rhomboedro

Ettersom alle ansiktene er de samme, er det nok å beregne området til en av dem og multiplisere det med seks.

Vi har at området til en rhombus kan beregnes av diagonalene med følgende formel med følgende formel

TIL_R = (DD)/2

Ved hjelp av denne formelen følger det at det totale arealet til Rhomboedro er

TIL_T = 6 (dd)/2 = 3DD.

Eksempel 3

Ansiktene til neste rhomboedro dannes av en rhombus hvis diagonal er d = 7 cm og d = 4 cm. Området ditt vil være

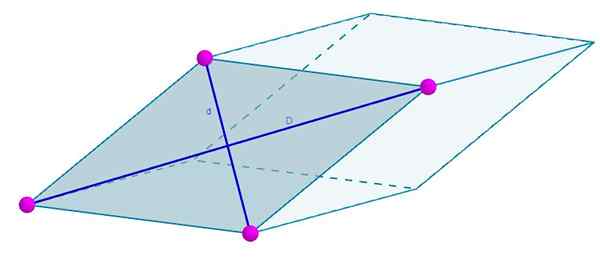
A = 3 (7 cm) (4 cm) = 84 cm².

Område av en rhomboiedro

For å beregne området til en rhomboiedro må vi beregne området til rhomboidene som utgjør det. Ettersom parallellepipedene oppfyller eiendommen som de motsatte sidene har samme område, kan vi knytte sidene i tre jevnaldrende.

På denne måten har vi at ditt område vil være

TIL_T = 2b₁h₁ + 2b₂h₂ + 2b₃h₃

Hvor b_Yo er basene assosiert med sidene og h_Yo dens relative høyde som tilsvarer nevnte baser.

Eksempel 4

Tenk på følgende parallellpiped,

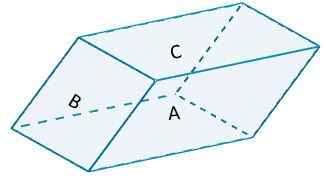
Hvor side A og side A '(deres motsatte side) er basert b = 10 og per høyde h = 6. Det markerte området vil ha en verdi av

TIL₁ = 2 (10) (6) = 120

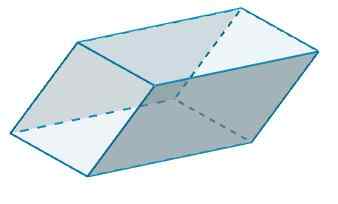
B og b 'har b = 4 og h = 6, deretter

TIL₂ = 2 (4) (6) = 48

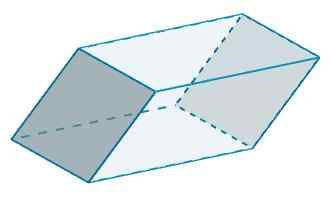
Og C og C 'har B = 10 og H = 5, også

TIL₃ = 2 (10) (5) = 100

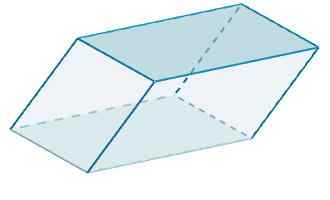
Endelig er Rhomboiedro -området

A = 120 + 48 + 100 = 268.

Volum av en parallellpiped

Formelen som gir oss volumet av en parallellpiped er produktet av området til et av ansiktene på grunn av høyden som tilsvarer nevnte ansikt.

V = a_Ch_C

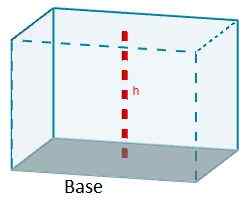
Avhengig av typen parallellpiped, kan denne formelen forenkles.

Dermed har vi for eksempel at volumet av en ortoedro vil bli gitt av

V = ABC.

Hvor A, B og C representerer lengden på ortoedrokantene.

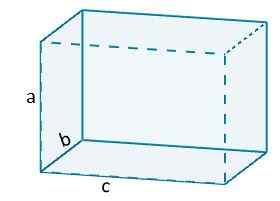
Og i det spesielle tilfellet med kuben er

V = a³

Eksempel 1

Det er tre forskjellige modeller for kakebokser, og du vil ha.

Den første er en kube hvis kant har en lengde på A = 10 cm.

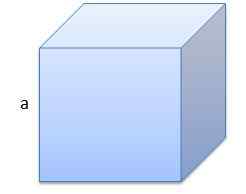
Volumet vil være V = 1000 cm³

Den andre er B = 17 cm, C = 5 cm, d = 9 cm.

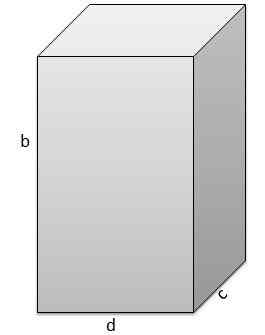
Og derfor er volumet V = 765 cm³

Og den tredje har E = 9 cm, f = 9 cm og g = 13 cm.

Og volumet er V = 1053 cm³

Kan tjene deg: typer vinkler, egenskaper og eksempler

Derfor er boksen med det største volumet den tredje.

En annen metode for å oppnå volumet til en parallellpiped er å ty til vektoralgebra. Spesielt det trippel skalære produktet.

En av de geometriske tolkningene av det trippel skalære produktet er den av volumet av parallellpiped, hvis kanter er tre vektorer som deler samme toppunkt som utgangspunkt.

På denne måten, hvis vi har en parallellpiped og vi vil vite hva volumet er, er det nok til å representere det i et koordinatsystem i R³ sammenfallende en av sine hjørner med opprinnelsen.

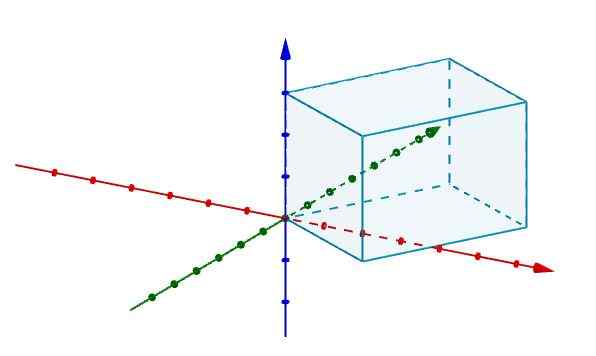
Så representerer vi kantene som stemmer overens med opprinnelsen med vektorer, som vist på figuren.

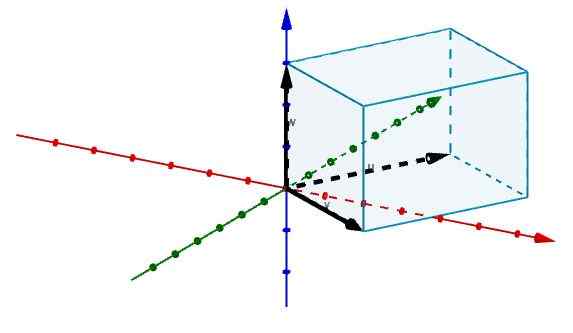
Og på denne måten har vi at volumet av nevnte parallellpiped er gitt av

V = | AXB ∙ C |

Eller tilsvarende, volumet er determinanten for 3 × 3 -matrisen, dannet av komponentene i kantvektorene.

Eksempel 2

Ved å representere følgende parallellpiped i r³ Vi kan se at vektorene som bestemmer at det er følgende

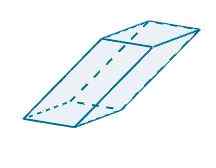
u = (-1, -3.0), v = (5, 0, 0) og w = (-0.25, -4, 4)

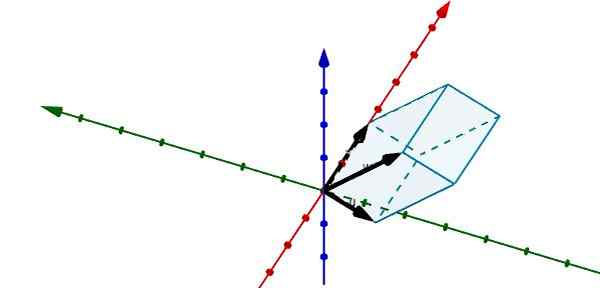
Bruke det trippel skalære produktet vi har

V = | (UXV) ∙ W |

Uxv = (-1, -3.0) x (5, 0, 0) = (0.0, -15)

(Uxv) ∙ w = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Dette konkluderer med at V = 60

Tenk nå følgende parallellpiped i r³ hvis kanter bestemmes av vektorene

A = (2, 5, 0), b = (6, 1, 0) og c = (3, 4, 4)

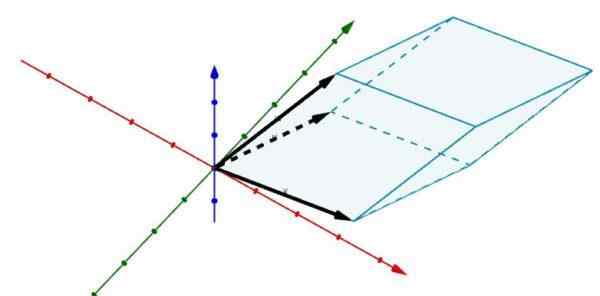
Å bruke determinanter gir oss det

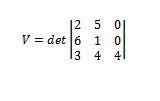
Dermed har vi at volumet av nevnte parallellpiped er 112.

Begge er likeverdige måter å beregne volumet på.

Perfekt parallellpiped

Det er kjent som Euler Brick (eller Euler -blokk) til en ortoedro som oppfyller eiendommen som både lengden på kantene og lengden på diagonalene til hvert av ansiktene er hele tall.

Mens Euler ikke var den første forskeren som studerte ortoedene som oppfyller den eiendommen, fant han interessante resultater om dem.

Den minste Euler-mursteinen ble oppdaget av Paul Halcke (1662-1731) og lengdene på kantene er A = 44, B = 117 og C = 240.

Et åpent problem i tallteorien er som følger:

Er det perfekte ortoeders?

For tiden har dette spørsmålet fortsatt ikke noe svar, siden det ikke har vært mulig å bevise at det ikke er noen kropper, men ingen er funnet.

Det som er demonstrert så langt, er at den perfekte parallellpiped gjør. Den første som blir oppdaget har som lengden på kantene verdiene 103, 106 og 271.

Referanser

1. Fyr, r. (1981). Uløste problemer i tallteori. Springer.
2. Landaverde, f. d. (1997). Geometri. Framgang.
3. Leithold, l. (1992). Beregningen med analytisk geometri. Harla, s.TIL.
4. Rendon, a. (2004). Teknisk tegning: Aktivitet Notatbok 3 2. Baccalaureate. Tebar.
5. Resnick, r., Halliday, d., & Krane, K. (2001). Vol -fysikk. 1. Mexico: Continental.