Pascalina eller Pascal Machine

Vi forklarer hva Pascalina, dens historie, egenskaper og funksjon er

Pascal de Pascal (1652). Kilde: Rama, CC BY-SA 3.0 Fr, via Wikimedia Commons

Hva er Pascalina?

De Pascalina Det er en mekanisk kalkulator, opprettet av den franske forskeren og filosofen Blaise Pascal (1623-1661), rundt 1642, med bare 19 år gammel. Navnet "Pascalina" ble gitt til ære for ham, selv om det også ble kalt "Arithmetic Machine".

Takket være et girsystem laget av jern og nøye artikulert, er Pascalina i stand til å legge til og trekke fra, og dermed være forløper for nåværende kalkulatorer. Og akkurat som disse har Pascalina et grensesnitt for innføring av data som i stedet for nøkler bruker en serie nummererte roterende plater, for å indikere posisjonsverdien til hvert siffer: enheter, titalls, hundrevis og mer.

De nummererte platene er utstyrt med hull, der en stang eller stilett blir introdusert for å snu dem gjennom trinn.

Den interne mekanismen består av en serie delikat koblede tannhjul, som beveger seg, trinn for trinn, sylindere med to tall med tall fra 0 til 9. Noen vinduer som er plassert på platene, tillater å observere verdiene som disse tallene skaffer seg, når du utfører en subtage eller subtraksjonsoperasjon.

Historie

Siden barndommen hadde Pascal allerede demonstrert sine store intellektuelle ferdigheter, så faren, sorenskriveren og matematikeren Etienne Pascal, bestemte seg for å gi ham best mulig utdanning. I 1642 ble Etienne Pascal sendt for å heve skatten i Rouen, Normandie, nord for Frankrike, et verk som ikke var lett.

Blaise Pascal, fast bestemt på å hjelpe faren, designet og bygde en maskin som ved bruk av mekaniske gir, var i stand til å rotere noen hjul for å utføre og vise operasjoner av summer og subtraksjon. Denne enheten ble kalt "Pascalina".

Blaise Pascal

Med Pascalina kunne multiplikasjoner og divisjoner også utføres, men ikke direkte, men gjennom påfølgende summer og subtraksjon.

Kan tjene deg: Sidereal eller Siderh Day

Kostnaden for å produsere Pascalina var imidlertid veldig høy, så oppfinnelsen gikk upåaktet hen av flertallet på den tiden. De som hadde råd til en, foretrakk å forlate den hjemme og ikke bruke det til rutinemessig arbeid, så nesten alle fortsatte å løse sin virksomhet på tradisjonell måte.

Mekanismen til Pascalina skal være veldig presis, slik at kalkulatoren fungerte riktig, men ofte sluttet å fungere. Og Pascal var den eneste som kunne reparere det hver gang dette skjedde.

Pascal fortsatte å forbedre utformingen de neste ti årene, og nådde rundt 50 Pascalinas, hvorav to er bevart: en er i Tyskland, i Zwinger -museet, i Dresde, Tyskland, og en annen i Musée des Arts et Métiers, i Paris.

Kjennetegn og funksjon av Pascalina

Pascalina har egenskaper som er felles for dagens kalkulatorer, som det fremgår av i begynnelsen. Den åpenbare forskjellen er at Pascalina jobber med mekaniske elementer, hvis justering må være perfekt, mens dagens kalkulatorer fungerer av elektronikk.

I utgangspunktet har Pascalina:

• Et grensesnitt for å legge inn dataene, bestående av skiver som drives av en stiletto.
• Den interne mekanismen som ble brukt til å behandle disse dataene, basert på gir og mobile dentas.
• Et panel som viser resultatene, med registreringsvinduer, for å sette pris på bevegelsen introdusert i skiven og observere resultatene.

Summen blir utført direkte, og flytter skiven for å introdusere hvert siffer av tilleggene. Subtraksjon gjøres imidlertid ikke direkte, men på en måte som i prinsippet er ganske nysgjerrig: Pascalino -komplementet, som er forklart nedenfor:

Komplement til 9 eller Pascalino komplement

Komplement til 9 er en numerisk teknikk som konverterer subtraksjoner til summer, lettere å løse med det mekaniske systemet implementert av Pascal.

Kan tjene deg: flytdiagram

For eksempel, hvis du vil løse operasjon A - B, legger det til “A” med Pascalino -komplementet til “B”, og resultatet av denne operasjonen er subtraksjonen som ble søkt.

Først forklares det hvordan du finner komplementet til 9 av et hvilket som helst nummer n. Det er veldig enkelt, det trekkes fra 9 hvert siffer av det tallet, som vist i følgende eksempler:

• La n = 20, komplement til 9 gjør: 99 - 20 = 79
• For n = 347, må du gjøre: 999 -347 = 652
• Hvis n = 7, er komplement til 9 2.

Subtraksjoner gjennom komplement til 9

Anta at du vil utføre følgende operasjon:

1246 - 822

Følgende trinn følges:

Trinn 1: Finn komplementet til 9 av de stjålne, som er 822, som er 999 - 822 = 177.

Steg 2: Utføre summen av minuenden og komplementet til 9 tidligere funnet: 1246 + 177 = 1423, observer godt til venstre i resultatet i resultatet.

Trinn 3: Den forespurte subtraksjonsoperasjonen er 423 + 1 = 424.

Leseren kan sjekke resultatet med en felles kalkulator!

Hvis minuenden er mindre enn avtrekking, fortsett for eksempel å utføre:

267 - 592

Trinn 1: Finn komplementet til 9 i avsnitt 592, som er 999 - 592 = 407.

Steg 2: Legg til minuend og komplement til 9 av de stjålne: 267 + 407 = 674.

Trinn 3: Beregn komplement til 9 av resultatet: 999 - 674 = 325

Trinn 4: Legg til det negative tegnet til resultatet: -325 og dette er den forespurte subtraksjonen.

Ved første øyekast virker det mer komplisert å lage en subtraksjon på denne måten, men med det bultehjulssystemet er det lettere.

Hvordan fungerer Pascalina?

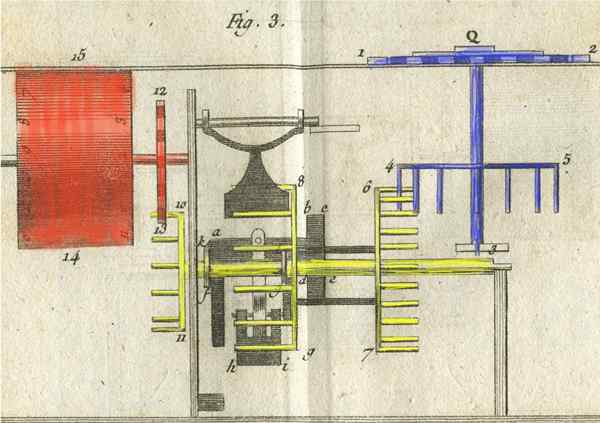
Intern mekanisme av Pascalina

Pascalina består i hovedsak av et girsystem som roterer 10 sylindere som indikerer tallene. Hver sylinder samler to serier med tall, og hver serie går fra 0 til 9.

Sylinderen til den ekstreme høyre indikerer enhetene, som følger dusinvis, følgende hundrevis og så videre. Når en av sylindrene dreier seg en fullstendig sving, gjør mekanismen den på venstre fremgang. Jo flere sifre figuren har, jo flere hjul og sylindere må de bevege seg, noe som gir en ide om den delikate av den indre mekanismen til Pascalina.

Kan tjene deg: 11 eksempler på feltforskning

Oppføringen av tallene gjøres gjennom skiven som er nummerert utenfor enheten, med en nål eller stilett, designet for dette formålet. Det er ringer for enheter, titalls, hundre og mer, tilsvarende hver av sylindrene.

Nå vil du se hvordan du utfører operasjonene.

Legg til

Anta at du vil utføre følgende operasjon med en Pascalina:

25 + 14

Med alle de initialiserte skivene i 0 beveger seg titalls 2 -enheter eller trinn, og enhetene til enhetene beveger seg i 5 trinn. Med dette introduseres det første å legge til.

Deretter beveger skiven på TENS 1 -enheten, og enhetene til 4. Resultatet er: 39.

Når en fullstendig sving blir tatt til 8 og hjulene legger de nødvendige omgangene til de øvre sifrene, for å vise resultatet.

Trekke fra

For å trekke fra, plasseres alle skiver til 9, siden mekanismen påvirker subtraksjonen ved komplement til 9, som indikert i foregående avsnitt. Brukeren trenger ikke å beregne komplementet, mekanismen gjør det av seg selv ved å initialisere DAL -ene med 9.

For eksempel vil du gjøre:

67 - 21

Det fortsetter på samme måte som i summen, det vil si at titallens skive er dreid i 6 trinn og enhetene er dreid i 7 trinn. På denne måten blir verdien av minuenden introdusert. Deretter blir titalls trinn og en av enhetene 1 dreid. Resultatet er 46, hvordan kan leseren sjekke.