Første balansetilstand Forklaring, eksempler, øvelser

De Første balansetilstand Det krever at sumptorvektoren til alle kreftene som virker på et legeme er ugyldig, slik at den er i ro (statisk balanse) eller med ensartet rettlinjet bevegelse (dynamisk likevekt).

Denne summen av krefter er ingen ringere enn nettokraften som virker på kroppen, og uttrykker denne modusen matematisk:

F_Nett = 0

∑ F = 0

Figur 1. Byggerne av antikken har allerede brukt den første likevektstilstanden, som det fremgår av Stonehenge -monumentet. Kilde: Pixabay.

I rommet gir den første likevektstilstanden til tre ligninger, en for hver dimensjon:

∑ f_x = 0; ∑ f_og = 0 og ∑ f_z = 0

Når disse ligningene er fornøyde, beveger objektet seg ikke, eller hvis det gjør det, vil det være med konstant hastighet.

Når vi observerer rundt oss, innser vi at vi kontinuerlig søker å tilfredsstille den første balansetilstanden slik at ting ikke faller.

Derfor søker den å kompensere for jordens gravitasjonsattraksjon gjennom støtte, tau eller støtte av noen, slik at ting forblir på plass og ikke går til bakken.

Andre ganger det som trengs er for å forhindre at eksterne elektromagnetiske felt forstyrrer driften av elektriske kretsløp og kommunikasjonsenheter. I så fall er det de elektriske ladningene som må være i balanse.

[TOC]

Eksempler

Et stort antall hverdagsobjekter tilfredsstiller den første likevektstilstanden, det er et spørsmål om å observere nøye:

Bygninger

Byggere søker stabilitet i konstruksjoner slik at brukere holder seg trygge. Målet med statisk er å studere forholdene for statisk balanse i bygninger, broer, veier og alle slags strukturer.

Higafor og hengende advarsler

Disse signalenhetene må forbli faste for å oppfylle sine funksjoner, derfor er de utsatt for kabler, innlegg og stenger på en slik måte at den første balansetilstanden er oppfylt.

Det kan tjene deg: Tredje lov om termodynamikk: Formler, ligninger, eksemplerFigur 2. Trafikklys og hengende advarsler er gjenstand på en slik måte at det tilfredsstiller den første likevektstilstanden. Kilde: PXFuel.

Elektrostbalansedriverepenthouse

Når ledende materialer som kobber og andre metaller skaffer seg elektrisk ladning, etableres den elektrostatiske balansen om kort tid, og etterlater belastningsoverskuddet på den ledende overflaten. Inne i det elektriske feltet er null.

Denne effekten brukes ofte til å isolere elektrisk og elektronisk utstyr til de ytre feltene, ved hjelp av det så -kalt Faraday -buret. Buret er laget av ledende materiale og omgir utstyret som skal beskyttes.

Under uvær fungerer biler som faradaybur ved å beskytte beboere mot elektriske støt.

Taklamper

I lyssystemer, for eksempel hengelamper, brukes den første balansetilstanden for å fikse dem på taket, på gulvet eller veggen.

Figur 3. Den forseggjorte taklampen kalt "edderkopper" tilfredsstiller den første likevektstilstanden. Kilde: Pixabay.

Bøker og gjenstander på tabeller

Objektene plassert på tabeller og hyller oppfyller den første balansetilstanden. Den normale kraften som støtten utøver på objektene er ansvarlig for å kompensere vekten.

Mål på viskositeten til en væske

For å bestemme viskositeten til en væske, en sfærisk gjenstand, med kjent diameter, som vil se hastigheten på grunn av motstanden, slippes innvendig. Hastigheten på sfæren er konstant, og er i dynamisk likevekt.

En større viskositet av væsken, mindre hastigheten som sfæren beveger seg inni.

Trinn for å anvende den første likevektstilstanden

-Lag et fritt kroppsdiagram, som viser alle kreftene som virker på kroppen (utelat hva kroppen utøver på andre).

Det kan tjene deg: Fysikk i middelalderen

-Velg et kartesisk koordinatsystem, og sikrer at kreftene om mulig er plassert på noen av aksene. Den positive adressen tas vanligvis i bevegelsen eller en mulig bevegelse.

-Bestem de kartesiske komponentene i hver kraft.

-Bruk Newtons andre lov for hver komponent, som etablert i begynnelsen, er det et ligningssystem.

-Løs systemet med ligninger hevet i forrige trinn.

Løste øvelser

- Trening løst 1

Figurens blokkering, av masse m, Den beveger seg nedover på vinkelplanet θ med konstant hastighet. Beregn verdien av den kinetiske friksjonen μ -koeffisienten_k, Hvis massen til blokken er M = 5 kg og θ = 37º.

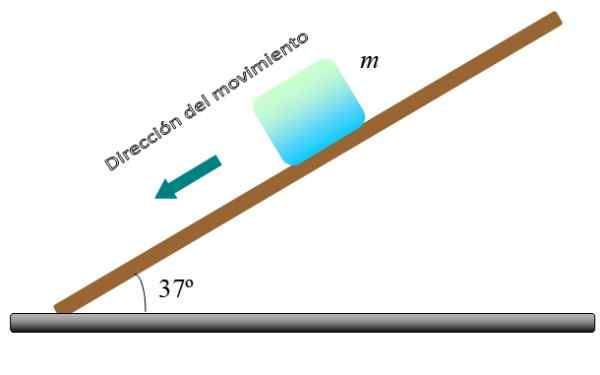Figur 4. En blokk glir med konstant hastighet på et skrå fly. Kilde: f. Zapata.

Løsning

Det første trinnet er å tegne det frie kroppsdiagrammet og velge et kartesisk koordinatsystem for å uttrykke hver kraftvektor. Kreftene som virker på blokken er:

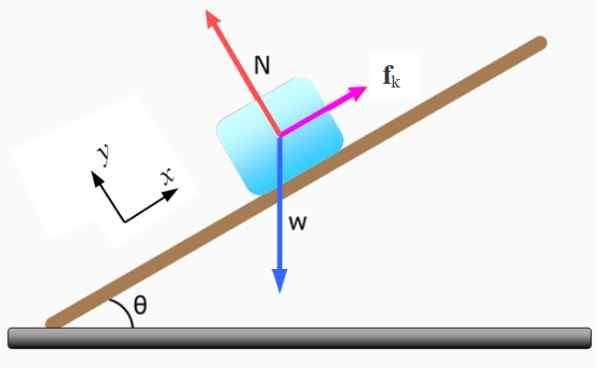Figur 5. Gratis kroppsdiagram for blokkering. Kilde: f. Zapata.

-Det normale N Utøvd av det skrå planet, det er vinkelrett på overflaten av dette.

-Vekten W Det er rettet vertikalt ned.

-Kinetisk friksjon F_k som motsetter seg bevegelse. Hvis den ikke eksisterte, ville kroppen bevege seg nedoverbakke med en akselerasjon lik g.Senθ.

Som vekt W Det er tilbøyelig med hensyn til de valgte koordinataksene, den må deles ned i de kartesiske komponentene:

W_x = mg.Sen 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
W_og = mg.cos 37º = 5 kg x 9,8 m/s² X cos 37º = 39.1 n

Newtons andre lov blir nå brukt, og samsvarer med hver sum til 0, siden blokken mangler akselerasjon når den beveger seg med konstant hastighet:

∑ f_og = N - w_og = 0
∑ f_x = W_x - F_k = 0

Størrelsen på kinetisk friksjon er proporsjonal med størrelsen på normalen, og er den kinetiske friksjonskoeffisienten μ_k Proporsjonalitetskonstanten.

Det kan tjene deg: absolutt trykk: formel, hvordan det beregnes, eksempler, øvelser

F_k = μ_k N

Samtidig:

N = w_og = 39.1 n

Og også:

F_k = W_x

Derfor:

29. 5 n = μ_k X 39.1 n

μ_k = 29. 5/39.1 = 0.75

- Trening løst 2

Beregn størrelsen på spenningene som støtter massetrafikklyset 33 kg, vist på figuren:

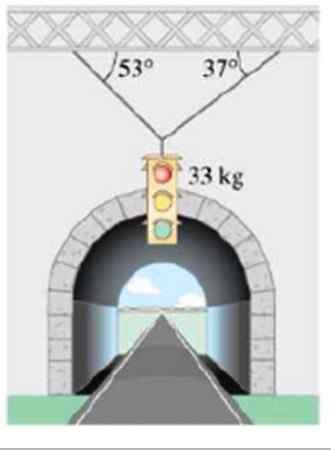Figur 6. Et trafikklys henger med kabler. Kilde: Giancoli. Fysikk med applikasjoner.

Løsning

Det frie kroppsdiagrammet gjøres både for trafikklyset og for knuten som holder kablene:

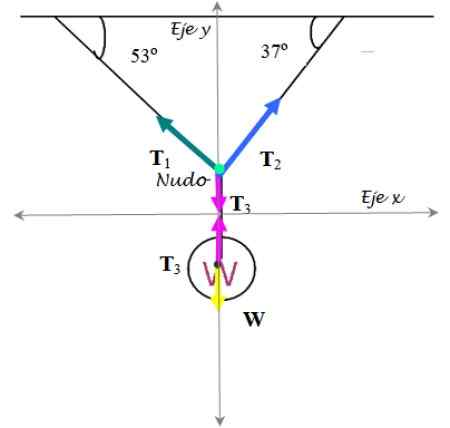Figur 7. Gratis kroppsdiagram for øvelsen løst 2. Kilde: f. Zapata.

Trafikklys

Om It Act: Spenningen t₃ opp og vekt w ned. Derfor:

∑ f_og = W - t₃ = 0

Derfor:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Knute

Spenninger brytes sammen i sine kartesiske komponenter:

∑ f_og = T₁ Sen 53º + t₂ Sen 37º - T₃ = 0
∑ f_x = T₂ Cos 37º - t₁ Cos 53º = 0

Og følgende system med lineære ligninger med to ukjente oppnås₁  og T₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

Løsningen av dette ligningssystemet er: t₁ = 258.7 n og t₂ = 194.0 n

Temaer av interesse

Likevektsforhold.

Andre likevektstilstand.

Referanser

1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
5. Wikipedia. Statisk (mekanisk). Gjenopprettet fra: er.Wikipedia.org.