Newtons første lovformler, eksperimenter og øvelser

De Newtons første lov, Også kjent som Inercia lov, Det ble først foreslått av Isaac Newton, fysisk, matematiker, filosof, teolog, oppfinner og alkymist. Denne loven etablerer følgende: "Hvis et objekt ikke blir utsatt for noen styrke, eller hvis kreftene som virker på det, kanselleres til hverandre, vil det fortsette å bevege seg med konstant hurtighet i en rett linje.""

I denne uttalelsen er nøkkelordet å være fortsette. Hvis lovene om loven er oppfylt, vil objektet fortsette med bevegelsen som den hadde. Med mindre en ubalansert styrke vises og endrer bevegelsestilstanden.

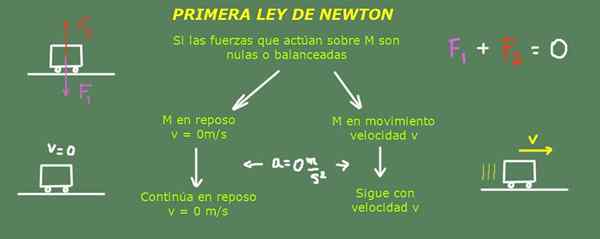
Forklaring av Newtons første lov. Kilde: Selvlaget.

Dette betyr at hvis objektet er i ro vil fortsette i ro, bortsett fra hvis en styrke tar den ut av denne tilstanden. Det betyr også at hvis et objekt beveger seg med en fast hastighet i rett retning, vil det fortsette å bevege seg slik. Vil bare endre seg når en ekstern agent utøver en styrke på ham og endrer hastigheten.

[TOC]

Bakgrunnen for loven

Isaac Newton ble født i Woolshorpe Manor (Storbritannia) 4. januar 1643 og døde i London i 1727.

Den nøyaktige datoen som Sir Isaac Newton oppdaget sine tre dynamikklover, er ikke kjent med sikkerhet, inkludert den første loven. Men det er kjent at det var lenge før publiseringen av den berømte boken Matematiske prinsipper for naturfilosofi, 5. juli 1687.

Diksjonen til Royal Spanish Academy definerer ordet treghet som følger:

""Eid av kroppene for å opprettholde deres hvilestatus eller bevegelse hvis det ikke er for handling av en styrke"".

Dette begrepet brukes også for å bekrefte at enhver situasjon forblir uendret fordi det ikke er gjort noen anstrengelser for å oppnå det, og noen ganger har ordet treghet rutinemessig konnotasjon eller forsømmelse.

Pre Newtonian Vision

Før Newton var de dominerende ideene til den store greske filosofen Aristoteles, som hevdet at for at et objekt skulle forbli i bevegelse, er det nødvendig at en styrke virker på den. Når styrken opphører, vil bevegelsen også gjøre det. Ikke slik, men selv i dag tror mange det.

Galileo Galilei, en strålende italiensk astronom og fysiker som bodde mellom 1564 og 1642, opplevde og analyserte kroppens bevegelse.

En av Galileos observasjoner var at en kropp som glir på en glatt og polert overflate med en viss innledende impuls, tar lengre tid å stoppe og har en større rute i en rett linje, i den grad friksjonen mellom kroppen og overflaten er lavere.

Det er tydelig at Galileo klarte ideen om treghet, men ikke formulerte en uttalelse så presis som Newton.

Kan tjene deg: Oversettelsesbalanse: Forhold, eksempler, øvelser

Her er noen enkle eksperimenter, som leseren kan utføre og bekrefte resultatene. Observasjoner vil også bli analysert i henhold til det aristoteliske synet på den Newtonske bevegelsen og visjonen.

Eksperimenter om treghet

Eksperiment 1

En boks fremmes på gulvet, og deretter blir drivkraften suspendert. Vi observerer at boksen reiser en liten reise til den stopper.

La oss tolke det forrige eksperimentet og resultatet, innenfor rammen av teoriene før Newton og deretter i henhold til den første loven.

I den aristoteliske visjonen var forklaringen veldig tydelig: boksen stoppet fordi styrken som beveget seg ble suspendert.

I Newtonian Vision kan ikke boksen på gulvet/gulvet fortsette å bevege seg med hastigheten den hadde på det tidspunktet at styrken ble suspendert, fordi mellom gulvet og boksen er det en ikke -balansert kraft, noe som gjør at hastigheten avtar til Boksen stopper. Dette er friksjonskraften.

I dette eksperimentet blir ikke lokalene til Newtons første lov oppfylt, så boksen stoppet.

Eksperiment 2 

Igjen er det boksen på gulvet/gulvet. Ved denne anledningen opprettholdes styrken på boksen, slik at friksjonskraften kompenserer eller balanserer. Dette skjer når vi får boksen til å fortsette konstant og i rett retning.

Dette eksperimentet motsier ikke den aristoteliske visjonen om bevegelsen: boksen beveger seg konstant fordi en styrke utøves på den.

Det motsier heller ikke Newtons tilnærming, fordi alle kreftene som virker på boksen er balansert. La oss se:

• I horisontal retning er kraften utøvd på boksen den samme og av retning i strid med friksjonskraften mellom boksen og gulvet.
• Da er nettokraften i horisontal retning null, det er grunnen til at boksen opprettholder hastigheten og retningen.

Også i vertikal retning er kreftene balansert, fordi vekten på boksen som er en kraft som peker vertikalt ned, blir nøyaktig kompensert av kontaktkraften (eller normal) som jorden utøver på boksen vertikalt oppover.

Forresten, vekten av boksen skyldes jordens gravitasjonsattraksjon.

Eksperiment 3

Vi fortsetter med boksen støttet på gulvet. I den vertikale retningen er kreftene balansert, det vil si at netto vertikal kraft er null. Det ville absolutt være veldig overraskende om boksen rykket opp.  Men i horisontal retning er det friksjonskraft.

Kan tjene deg: Mekanisk fordel: Formel, ligninger, beregning og eksempler

Nå, for at forutsetningen om Newtons første lov skal oppfylles, må vi redusere friksjonen til det minste uttrykket. Dette kan oppnås ganske omtrent hvis vi ser etter en veldig glatt overflate som vi sprayet silikonolje.

Når silikonolje reduserer friksjonen nesten til null, så når denne boksen er horisontalt, vil den opprettholde hastigheten og retningen med en lang seksjon.

Det er det samme fenomenet som oppstår med en skater på et isspor, eller med ishockey -disken når de er kjørt og slipper på egen konto.

I de beskrevne situasjonene, der rubb.

I den aristoteliske visjonen kunne dette ikke skje, for i henhold til denne naive teorien oppstår bevegelsen bare når det er en nettokraft på objektet i bevegelse.

Isoverflaten kan vurderes med veldig liten friksjon. Kilde: Pixabay.

Forklaring av Newtons første lov

Treghet og masse

Massen er en fysisk mengde som indikerer mengden materie som inneholder en kropp eller gjenstand.

Massen er da en egen egenskap av materie. Men materien er sammensatt av atomer, som har en masse. Massen til atomet er konsentrert i kjernen. Det er protonene og nøytronene til kjernen som praktisk talt definerer atomets og materielle massen og materien.

Massen måles vanligvis i kilo (kg), det er den grunnleggende enheten til International Units System (SI).

Prototypen eller referansen til KG er en platina- og iridiumsylinder som er lagret på det internasjonale kontoret for vekter og tiltak i Sèvres i Frankrike, selv om den i 2018 var knyttet til Planck Constant og den nye definisjonen trer i kraft fra 20. mai 2019.

Vel, det hender at treghet og deig er relatert. En større masse, større treghet har et objekt. Det er mye vanskeligere eller dyrt når det gjelder energi å endre bevegelsestilstanden til en mer massiv enn en annen mindre massiv.

Eksempel

For eksempel kreves det mye mer styrke og mye mer arbeid for å ta en eske med ett tonn (1000 kg) fra hvile enn en annen kilo (1 kg). Det er derfor det vanligvis sies at den første har mer treghet enn den andre.

På grunn av forholdet mellom treghet og masse, innså Newton at hastigheten ikke er representativ for bevegelsestilstanden. Det er grunnen til at han definerte et beløp kjent som mengde bevegelse enten Momentum som er betegnet med tekstene p Og det er produktet av massen m For hastighet v:

Det kan tjene deg: Grashof Law: Saker, mekanismer, eksempler, applikasjoner

 p = m v

Den dristige i p og i v De indikerer at dette er fysiske mengder av vektor, det vil si at de er mengder med størrelse, retning og mening.

I stedet massen m Det er en skalær mengde, som tildeles et tall som kan være større enn eller lik null, men aldri negativt. Inntil i dag er det ikke funnet et objekt med negativ masse.

Newton brakte fantasien og abstraksjonen til det ekstreme, og definerte samtalen Gratis partikkel. En partikkel er et materialpunkt. Det vil si at det er som et matematisk punkt, men med masse:

En fri partikkel er at partikkel som er så isolert, så langt fra et annet objekt i universet at ingenting kan utøve noe samspill eller styrke over det.

Senere fortsatte Newton å definere treghetsreferansesystemene, som vil være de der de tre lovene deres blir brukt. Her er definisjonene i henhold til disse konseptene:

Treghetsreferansesystem

Hvert koordinatsystem knyttet til en fri partikkel, eller som overføres med konstant hastighet med hensyn til den frie partikkelen vil være et treghetsreferansesystem.

Newtons første lov (treghetslov)

Hvis en partikkel er gratis, har den en konstant bevegelsesmengde med hensyn til et treghetsreferansesystem.

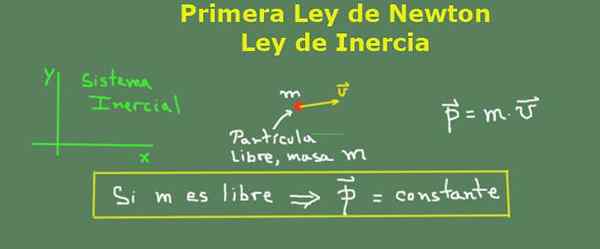Newtons første lov og bevegelsesmengde. Kilde: Selvlaget.

Løste øvelser

Oppgave 1

Et hockeyalbum er 160 gram på ishallen på 3 km/t. Finn mengden av bevegelse.

Løsning

Massen til albumet i kilo er: M = 0.160 kg.

Hastigheten i meter over sekundet: V = (3/3.6) m/s = 0.8333 m/s

Mengden bevegelse eller momentum p beregnes som følger: p = m*v = 0.1333 kg* m/s,

Oppgave 2

Friksjon på det forrige albumet regnes som ugyldig, så momentumet er bevart mens ingenting endrer albumets rette kurs. Imidlertid er det kjent at to krefter opptrer på albumet: vekten av platen og kontaktkraften eller normal som gulvet utøver på det.

Beregn verdien av normal kraft i Newtons og dens retning.

Løsning

Når momentumet er bevart, må den resulterende kraften på hockeyalbumet være null. Vekten peker vertikalt ned og OK: P = m *g = 0.16 kg * 9.81 m/s²

Normalkraften må nødvendigvis motvirke vekten, så den må registrere seg vertikalt opp og størrelsen på det vil være 1.57 n.

Artikler av interesse

Newtons loveksempler i det virkelige liv.

Referanser

1. Alonso m., Finn e. Fysikkvolum I: Mekanikk. 1970. Inter -American Education Fund s.TIL.
2. Hewitt, p. Konseptuell fysisk vitenskap. Femte utgave. Pearson. 67-74.
3. Young, Hugh. Universitetsfysikk med moderne fysikk. 14. utg. Pearson. 105 - 107.