Relative søskenbarn hva er, forklaring, eksempler

Er kalt relative søskenbarn (Coprmimos eller søskenbarn i forhold til hverandre) til alle par av hele tall som ikke har noen felles divisor, bortsett fra 1. Med andre ord, to hele tall er relative søskenbarn hvis de i deres sammenbrudd i primtall har ingen felles faktor.

For eksempel, hvis 4 og 25 er valgt, er nedbrytningene i primefaktorer for hver henholdsvis 2² og 5². Som det kan sees, har de ingen felles faktor, derfor er 4 og 25 relative søskenbarn.

På den annen side, hvis du velger 6 og 24, når du gjør sammenbruddet i primefaktorer, oppnås det at 6 = 2*3 og 24 = 2³*3.

Som det kan sees, har disse to siste uttrykkene minst en vanlig faktor, derfor er de ikke relative søskenbarn.

Kjennetegn på relative søskenbarn

En detalj som omsorg må.

På den annen side kan definisjonen ovenfor oppsummeres som følger: to heltall “a” og “b” er relative søskenbarn hvis, og bare den maksimale vanlige divisoren for disse er 1, det vil si MCD (A, B ) = 1.

To umiddelbare konklusjoner av denne definisjonen er at:

-Hvis "A" (eller "B") er et primtall, så MCD (A, B) = 1.

-Hvis "A" og "B" er primtall, så MCD (A, B) = 1.

Det vil si at hvis minst et av de valgte tallene er et primtall, er antallet av tall relative søskenbarn.

Andre funksjoner

Andre resultater som brukes til å avgjøre om to tall er relative søskenbarn er:

-Hvis to hele tall er påfølgende, er dette relative søskenbarn.

-To naturlige tall "a" og "b" er relative søskenbarn hvis, og bare hvis tallene "(2^a) -1" og "(2^b) -1" er relative søskenbarn.

-To hele tall "a" og "b" er relative søskenbarn hvis, og bare hvis, når du grafering av punktet (a, b) i det kartesiske planet, og bygger linjen som passerer gjennom opprinnelsen (0,0) og (a , b), dette inneholder ikke noe poeng med hele koordinater.

Eksempler

1.- Tenk hele nummer 5 og 12. Nedbrytningene i primefaktorer for begge tall er: henholdsvis 5 og 2²*3. Avslutningsvis er MCD (5,12) = 1 derfor 5 og 12 relative søskenbarn.

2.- La tallene -4 og 6. Deretter -4 = -2² og 6 = 2*3, slik at MCD (-4,6) = 2 ≠ 1. Avslutningsvis -4 og 6 er ikke relative søskenbarn.

Hvis linjen som går gjennom de bestilte parene (-4,6) og (0,0), og for å bestemme ligningen av nevnte linje, kan bekreftes at dette passerer gjennom punktet (-2,3).

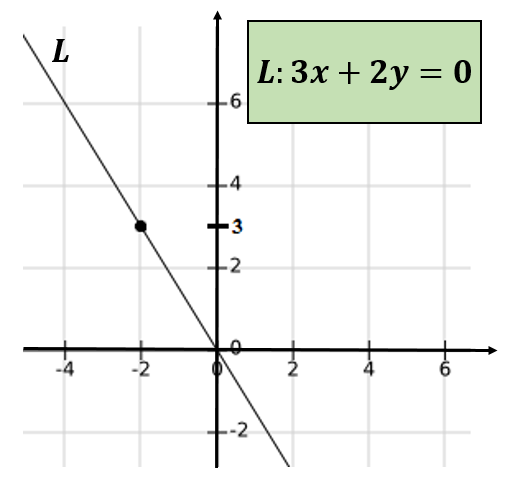
Igjen er det konkludert med at -4 og 6 ikke er relative søskenbarn.

3.- Nummer 7 og 44 er relative søskenbarn og kan avsluttes raskt takket være det som er sagt ovenfor, fordi 7 er et primtall.

4.- Tenk på tall 345 og 346. Som to påfølgende tall er det bekreftet at MCD (345.346) = 1, derfor er 345 og 346 relative søskenbarn.

5.- Hvis tall 147 og 74 blir vurdert, er dette relative søskenbarn, siden 147 = 3*7² og 74 = 2*37, derfor MCD (147,74) = 1.

6.- Tall 4 og 9 er relative søskenbarn. For å demonstrere det kan du bruke den andre karakteriseringen som er nevnt ovenfor. Faktisk 2^4 -1 = 16-1 = 15 og 2^9-1 = 512-1 = 511.

Tallene som er oppnådd er 15 og 511. Nedbrytningene i primefaktorer av disse tallene er henholdsvis 3*5 og 7*73, slik at MCD (15.511) = 1.

Som du ser, er det å bruke den andre karakteriseringen et lengre og mer arbeidskrevende arbeid for å bekrefte det direkte.

7.- Tenk på tallene -22 og -27. Da kan disse tallene skrives om som følger: -22 = -2*11 og -27 = -3³. Derfor er MCD (-22, -27) = 1, SO -22 og -27 relative søskenbarn.