Hva er algebraiske uttrykk og som er de hyppigste?

De algebraiske uttrykk De er matematiske termer som inneholder tall og bokstaver. I kombinasjon med symbolene på matematiske operasjoner tillater de å skaffe formler eller ligninger, fra beskrivelser laget av ord. 

På sin side kan disse bokstavene legges til, trekkes fra, multiplisert eller deles med andre tall, som kan være eksplisitt eller også representert med bokstaver.

Figur 1. Eksempler på algebraiske uttrykk

[TOC]

Hva er algebraiske uttrykk for?

For eksempel uttrykket:

2x + 3 

Det er et algebraisk uttrykk, der bokstaven "x" representerer et tall som er ukjent eller som kan ta forskjellige verdier.

Hva er fordelen med å bruke et algebraisk uttrykk i stedet for å si: "To ganger et tall lagt til 3"?

For det første opptar algebraisk uttrykk mindre plass. Og hvis x ikke er et fast antall, kan det gis forskjellige verdier til "x" for å oppnå forskjellige resultater av dette uttrykket.

Dette er kjent som den numeriske verdien av algebraisk uttrykk.

For eksempel, hvis x = 1, er resultatet 2⋅1 + 3 = 2 + 3 = 5

I stedet, gjør x = -2, viser uttrykket å være 2⋅ (-2) + 3 = -4 + 3 = -1

I en annen type anvendelse representerer algebraiske uttrykk en ligning eller likhet som må løses for å vite verdien av antallet som er representert med bokstaven.

Her har vi en enkel lineær ligning:

2⋅x + 3 = 7

Løsningen på denne ligningen, som forresten også er et algebraisk uttrykk, er:

x = 2

Siden multiplisering 2 med 2 gir 4 pluss 3 gir resultatet: 7. Men det er lettere å forstå når et algebraisk uttrykk brukes i stedet for å beskrive alt med ord.

Hyppigste algebraiske uttrykk

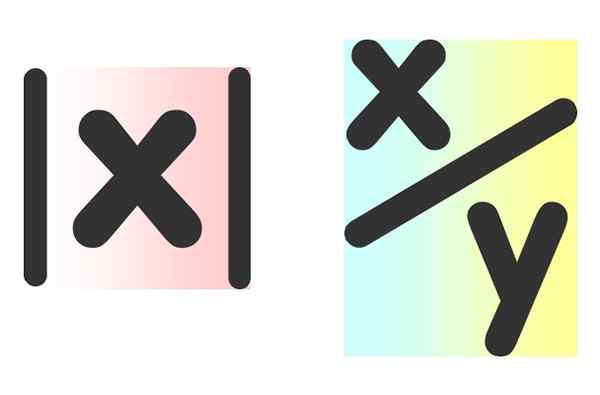Figur 2. Ukjente beløp symboliserer ofte med bokstavene "x" og "y". Til venstre er den absolutte verdien av et tall og til høyre kvotienten i to tall. Kilde: Pixabay.

Algebraiske uttrykk er mye brukt i matematikk, vitenskap, økonomi og administrasjon.

Nedenfor er en liste over uttrykk som vises veldig ofte i matematikk og andre fag, der det blir bedt om et forslag blir bedt om eller løst.

Det kan tjene deg: omkretsen av sirkelen: Hvordan ta den ut og formler, løste øvelser

Vanligvis er et ukjent eller ukjent nummer betegnet som "x", men vi kan bruke hvilken som helst annen alfabetbrev som avtalt.

Det bør også huskes at det i et algebraisk uttrykk kan ha involvert mer enn en verdi, ukjent eller variabel, så hver og en skal tildeles et annet bokstav.

Liste over algebraiske uttrykk

-Den doble eller dobbelte av et tall: 2x

-Dupelen til et tall flere enheter: 2m + 3

-Den tredje delen av et tall: z/3

-To ganger et tall bortsett fra den tredje delen: 2x - x/3

-Kvadratet på et tall: x²

-Kvadratet med et antall mer av dette tallet: x² + 2x

-Duppen på kvadratet på et tall: 2x²

-Et momentnummer: 2n

-Et oddetall: 2n + 1

-Tre påfølgende tall: x, (x+1), (x+2)

-Tre påfølgende til og med tall: 2n, 2n +2, 2n +4

-Tre påfølgende oddetall, 2n + 1, 2n + 3, 2n + 5

-Et visst tall lagt til på sammenheng: x +(x +1) = 2x +1

-Halvparten av påfølgende av et heltall: (x+1)/2

-Trippel av halvparten av et tall på et tall: 3. (1/2) x² = (3/2) x²

-Halvparten av ett antall til: X/2 + Y/3

-Den tredje delen av produktet mellom kvadratet på et tall og et annet tall som enheten ble trukket fra: (1/3) x².(Y-1)

-Et tall og det motsatte: a, -a

-Et tall og dets inverse: a, 1/a

-Summen av et tall med sin påfølgende forhøyet til torget: x + (x + 1)²

-Trekk 7 til to ganger et visst antall høyt til torget: (2x)² - 7

-To tall som når multiplisert gir 24: P.Q = 24

Kan tjene deg: vinkelforskyvning

-Den absolutte verdien av et tall: │x│

-Kvotienten mellom to tall: x/y

-Kvadratroten av produktet av to tall: √x.og

Figur 3. Dette algebraiske uttrykket blir lest som "kvadratroten til produktet av to tall x og y". Kilde: Pixabay.

-Ett tall som overstiger et annet i 30 enheter: x = y +30

-To ganger et tall som halvparten hans trekkes fra: 2x- x/2

Verbale problemer og deres algebraiske uttrykk

- Oppgave 1

Halvparten av en ku veier 100 kg mer enn veier en fjerdedel av samme ku. Hvor mye veier kua?

Svar

For det algebraiske uttrykket av dette problemet, kaller vi x vekten av kua.

Halvparten av kua veier ½ x. Fjerde del av kua veier ¼ x. Til slutt er det algebraiske uttrykket som tilsvarer: "Halvparten av kua veier 100 kg mer enn et kvarter" er:

½ x = ¼ x + 100

For å vite hvor mye kua veier, må du gruppere vilkårene med X på venstre side og la 100 være til høyre:

(½ --¼) x = 100

¼x = 100

x = 400 kg

Kua veier 400 kg.

- Oppgave 2

På en gård er antall kaniner dobbelt så mange kyr. Hvis antall kyr er 10. Hvor mange kaniner er det?

Svar

Hvis C er antall kaniner og V er antall kyr, er det algebraiske uttrykket for uttalelsen:

C = 2⋅V

V = 10

Så å erstatte verdien av V i den første av ligningene den oppnås:

C = 2 ⋅ 10 = 20

Det vil si at gården har tjue kaniner.

- Oppgave 3

Hva er tallet multiplisert med syv og trekker fra seks gir tjue -nine?

Svar

Hvis vi kaller dette ukjente nummer X, kan dette algebraiske uttrykket heves:

Kan tjene deg: Assosiativ eiendom: sum, multiplikasjon, eksempler, øvelser

7x - 6 = 29

På 6 venstre side passerer den til høyre side av likhet med et endret tegn:

7x = 29 + 6 = 35

Det følger at x = 35/7 = 5

- Oppgave 4

To ganger blir et visst tall 13 trukket fra og 7 er 7. Hva er nummeret?

Svar

Hvis vi kaller det nummeret X, er det algebraiske ligningen:

2 x - 13 = 7

Hva er verdien av 2x ?

Svaret er at 2x må være (13 + 7) slik at når du fjerner 13 er det 7.

Dette betyr at 2x må være lik 20, det vil si:

2x = 20

Tallet x som multiplisert med 2 da 20 er 10, derfor:

x = 10

- Oppgave 5

To påfølgende heltall legger opp 23. Foreslå en algebraisk ligning som gjør det mulig å bestemme nummeret og finne det.

Svar

Anta at det første av tallene er n, så den som følger er n+1 og summen av disse to er n+(n+1). Det er også kjent at summen av summen er 23, så er ligningen skrevet:

n + (n + 1) = 23

Løsningen oppnås først forenkle venstre side av likhet:

2 n + 1 = 23

Deretter blir 2 N ryddet av 1 til høyre medlem med det endrede tegnet:

2 n = 23 - 1

Høyre medlem er løst:

2 n = 22

Neste, n, og passerer de 2 som multipliserer medlemmet av venstre som deler medlemmet av høyre:

N = 22/2

Og det endelige resultatet oppnås:

N = 11

Referanser

1. Baldor, a. Algebra. Sentralamerikansk kulturell redaksjon C.TIL.
2. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
3. Cimanet. Algebraiske uttrykk. Gjenopprettet fra: Cinamet.Uoc.Edu
4. Guzman s. Algebraiske uttrykk. Hentet fra: Finitionsbegrep.av
5. Quiz. Algebraiske uttrykk. Gjenopprettet fra: kanskje.UPRM.Edu
6. Martha. Eksempler på algebraiske uttrykk. Gjenopprettet fra: Superprof.er