Hva er trekantede tall? Egenskaper og demonstrasjoner

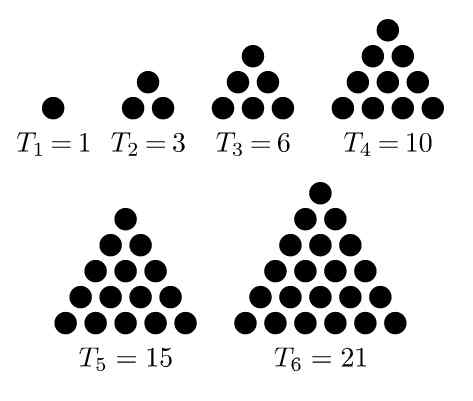
Det er kjent som trekantede tall til sekvensen av tall som oppnås ved å lage et arrangement eller figur av punkter med likestående trekant. Den første av sekvensen er: 1, 3, 6, 10, 15, 21, ..

Det første trekantede problemet er 1, det andre er 3, fordi den oppnås fra å legge en to -punkts rad til den forrige, for å danne en liksidig trekant på tre elementer.

Figur 1. Sekvens av de seks første trekantede tallene. Kilde: Wikimedia Commons. Melchoir/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)

Den tredje er 6, som vises når du legger til en trepunktsrekke til forrige arrangement, slik at en tre -punkts trekant dannes per side. 10 av sekvensen oppnås ved å legge til en annen rad til forrige arrangement slik at det dannes en fire -punkts trekant per side.

Formelen som lar deg finne elementet n Fra den trekantede sekvensen, kjent, er det fremre trekantede tallet:

T_n = T_N-1 + n

Listen over de seks første trekantede tallene oppnås slik:

-Først: 1

-Sekund: 1 + 2 = 3

-Tredje: (1 +2) + 3 = 3 + 3 = 6

-Rom: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Femte: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Sjette: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Egenskaper for trekantede tall

1.- N-Simo TN-trekantet antall av den trekantede tallsekvensen er halvparten av n multiplisert med n+1:

T_n = ½ n (n+1)

2.- Summen av det trekantede tallet n-ésimo med det fremre trekantede tallet, det vil si (n-1) -Sheimo, det er kvadrat forhøyet:

T_n + T_N-1= n²

3.- Forskjellen i det trekantede tallet n-dette mindre den trekantede n-ésimo mindre en er n:

T_n - T_N-1 = n

4.- Summen av de første trekantede tallene kalles det tetrahedrale tallet SN og er lik den sjette delen av produktet multiplisert med (n + 1) og multiplisert med (n + 2):

Kan tjene deg: beskatning

S_n= ⅙ n (n + 1) (n + 2)

5.- Hvert naturlig tall n er resultatet av summen av tre trekantede tall:

N = Δ1 + Δ1 + Δ3

Denne siste eiendommen eller teoremet ble oppdaget av den store matematikeren Carl Friedrich Gauss i 1796, som han scoret i dagboken sin ved å plassere den greske beundringen Eureka! hva betyr det "Jeg har oppnådd det".

Det var det samme ordet som ble brukt mye tidligere av de greske arkimedene da han bestemte den tilsynelatende vekten av en nedsenket kropp.

I dette forholdet blir nulltallet tatt som trekantet, og det kan være repetisjon.

Demonstrasjoner

- Demonstrasjon 1

Bevise at det trekantede nummeret n-Dette er:

T_n = ½ n (n+1)

Det er lett å utlede den forrige formelen, hvis vi innser at vi kan legge til samme antall poeng til det trekantede arrangementet for å danne en firedobling av poeng.

Ettersom det totale antall arrangementspunkter i form av en firkantet er antall rader n multiplisert med antall kolonner (N+1), Da vil det trekantede arrangementet bare ha halvparten av ordningens punkter i form av en firedoblet.

Her er illustrert i figur 2.

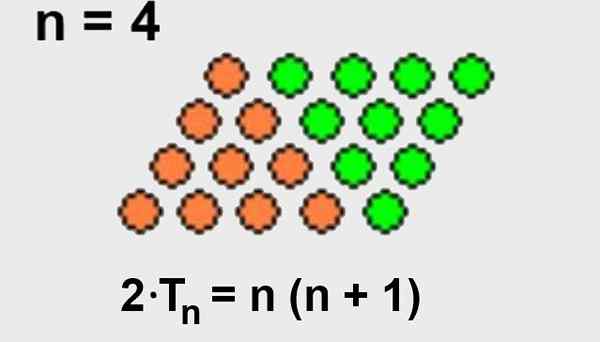Figur 2. Firkantet -formet arrangement der det totale antall poeng er antall rader n multiplisert med antall kolonner n+1. Det totale antall poeng er også det dobbelte av det trekantede arrangementet. Kilde: Wikimedia Commons.

- Demonstrasjon 2

Demonstrere at summen av n-Dette trekantede nummeret med n-Jo mindre en trekantet nummer er n kvadrat:

T_n + T_N-1= n²

Det er allerede vist at det trekantede nummeret n-Dette er gitt av:

T_n= ½ n (n+1)

Derfor er det fremre trekantede tallet:

T_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Summen av begge gjenstår:

T_n + T_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ n tas for å oppnå:

T_n + T_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

Og umiddelbart blir uttrykket forenklet inne i braketten:

Det kan tjene deg: estimering etter intervaller

T_n + T_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Nå, husker at ½ for 2 er 1 og at n for n er n kvadrat, har du:

T_n + T_N-1 = n²

Denne egenskapen kan også demonstreres geometrisk, trekanten er ganske enkelt fullført for å danne en firkant, som vist i figur 3.

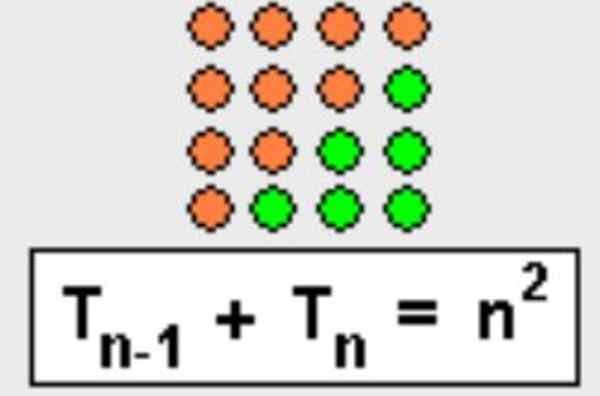Figur 3. Summen av n-ésimo trekantet nummer med det fremre trekantede tallet er lik N-kvadrat. Kilde: Wikimedia Commons.

- Demonstrasjon 3

Forskjellen i det trekantede antall ordre n minus det trekantede antall bestilling N-1 er n:

T_n - T_N-1 = n

Dette kan testes ganske enkelt ved å huske at følgende trekantede tall oppnås fra det forrige gjennom formelen:

T_n = T_N-1 + n

Og derfra er det tydelig at T_n - T_N-1 = n. Det er også enkelt å visualisere det grafisk, som vist i figur 4.

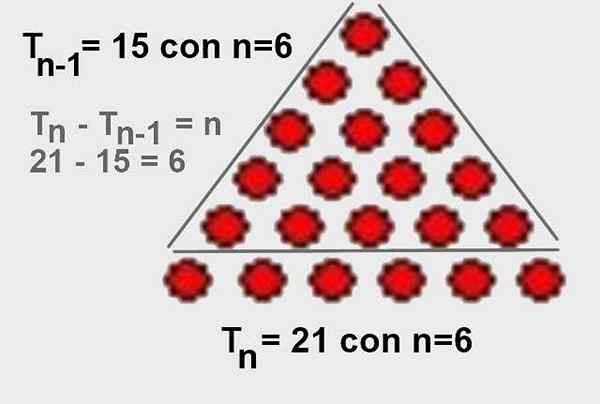Figur 4. Forskjellen på det trekantede antall ordre n mindre det fremre trekantede orden n-1 er n. Kilde: Wikimedia Commons.

- Demonstrasjon 5

Summen av de første trekantede N -tallene sn Det er lik den sjette delen av produktet multiplisert med (n + 1) og multiplisert med (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

La oss bruke det trekantede antall ordre n: T_n= ½ n (n+1). Summen av den første n Trekantede tall vil betegne det for S_n  

For eksempel, S₁ betyr summen av det første trekantede problemet, som utvilsomt vil være 1.

La oss så se om formelen vi prøver å prøve blir overholdt n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Faktisk er formelen for n = 1 sjekket. Det er lett å visualisere at summen av n+1 første trekantede tall vil være summen av det første n mer det neste trekantede tallet:

S_N+1 = S_n + T_N+1

Anta nå formelen til S_n Det er oppfylt for n, så erstatter vi det i forrige uttrykk og legger til det trekantede antall ordre N+1:

S_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]

Kan tjene deg: vinkelrett linje: egenskaper, eksempler, øvelser

La oss se trinn for trinn hva som oppnås:

-Vi utfører summen av de to fraksjonelle uttrykkene:

S_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Den fjernes fra telleren som er vanlig til 2 (n + 1) (n + 2) og forenkler:

S_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Det forrige resultatet stemmer overens med S -formelenn Hvis n+1 erstattes, som har blitt demonstrert ved induksjon, formelen til summen av de første trekantede termer.

Tetrahedralt nummer

Resultatet som er oppnådd kalles Tetrahedralt antall ordre n, Fordi det er som å akkumulere trekantede lag som danner en tetrahedron, som vist i følgende animasjon.

Figur 5. Summen av n trekantede tall tilsvarer bunken med lag av n, n-1, ..., 1 trekanter som danner en vanlig tetrahedron. Kilde: Wikimedia Commons.

Referanser

1. Camacho J. Et intetanende utseende av trekantede tall. Gjenopprettet fra: Masscience.com
2. Claudio. Trekantede tall. Gjenopprettet fra: ganske enkelt tall. Blogspot. com
3. Wikipedia. Trekantet nummer. Gjenopprettet fra: er.Wikipedia.com
4. Wikipedia. Trekantet nummer. Hentet fra: i.Wikipedia.com
5. Wikipedia. Antall tretrahedral. Hentet fra: i.Wikipedia.com