Hva er Coplanares -vektorer? (Med løste øvelser)

De Coplanares vektorer O Coplanarios er de som er inneholdt på samme plan. Når du bare har to vektorer, er disse alltid koblet.

Hvis du har tre eller flere vektorer, kan det være at noen av dem ikke er i samme plan som andre, derfor kunne de ikke betraktes som Coplanares. Følgende figur viser et sett med koplaner betegnet i fetvektorer TIL, B, C og D:

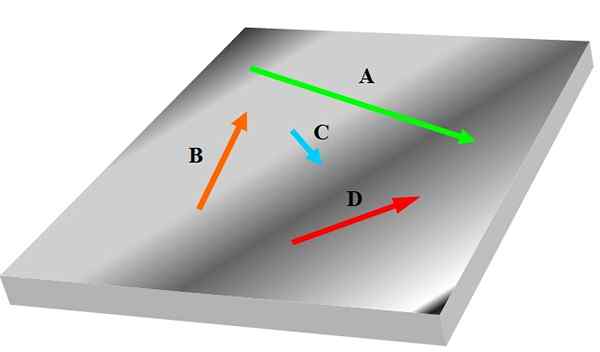Figur 1. Fire koplaner. Kilde: Selvlaget.

Vektorer er relatert til atferden og egenskapene til relevante fysiske størrelser i vitenskap og ingeniørfag; For eksempel hastighet, akselerasjon og styrke.

En kraft gir forskjellige effekter på et objekt når måten den brukes på er variert, for eksempel endret intensitet, retning og mening. Fremdeles endrer en av disse parametrene resultatene er betydelig forskjellige.

I mange applikasjoner, både i statisk og dynamikk, er kreftene som virker på et legeme på samme plan, derfor anses de som Coplanares.

[TOC]

Betingelser for at vektorer skal være koplaner

For at tre vektorer skal være Coplanares, må de være på samme plan, og dette skjer hvis de oppfyller noen av følgende forhold:

-Vektorer er parallelle, derfor er komponentene deres proporsjonale og er lineært avhengige.

-Det blandede produktet ditt er ugyldig.

-Hvis du har tre vektorer og noen av dem kan skrives som en lineær kombinasjon av de to andre, er disse vektorene Coplanares. For eksempel en vektor som er resultatet av summen av to andre, er de tre alle i samme plan.

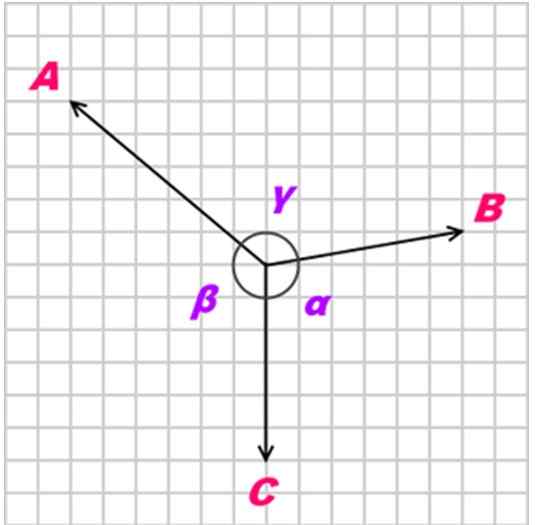
Kan tjene deg: voltmeter: egenskaper, drift, hva er det for, typer

Alternativt kan tilstanden til koplanaritet etableres som følger:

U v w De er koplaner hvis det er tre tall (skalarer) α, β, y slik at αeller + βv + γW = 0 Med (α, β, γ) forskjellig fra (0, 0, 0)

Blandet produkt mellom tre vektorer

Det blandede produktet mellom vektorer er definert med tre vektorer eller, v og W, noe som resulterer i en skalar som følger av å utføre følgende operasjon:

eller · (v x W) = eller · (v x W)

Først er kryssproduktet som er i parenteser laget: v x W, hvis resultat er en normal (vinkelrett) vektor til planet der de er slik v som W.

Ja eller er på samme fly som v og W, Naturligvis skal skalarproduktet (punktprodukt) mellom U og nevnte normal vektor være 0. På denne måten blir det bekreftet at de tre vektorene er Coplanares (de ligger på samme plan).

Når det blandede produktet ikke er null, tilsvarer resultatet volumet til parallellpiped som har vektorene eller, v og W som tilstøtende sider.

applikasjoner

Coplanares, samtidig og ikke -kolineale krefter

Styrkene samtidig De blir alle brukt på samme punkt. Hvis de også er koplaner, kan de bare erstattes av en, som kalles resulterende kraft Og den har samme effekt som de opprinnelige kreftene.

Hvis en kropp er i likevekt takket være tre koplaner, kalt samtidig og ikke -kolineale (ikke -parallelle) krefter, kalt TIL, B og C, han Lamys teorem Han påpeker at forholdet mellom disse kreftene (størrelsesorden) er som følger:

A / sin α = b / sen β = c / sen γ

Med α, β og γ som vinklene imot de påførte kreftene, som vist i følgende figur:

Figur 2. Tre krefter A, B og C Coplanares virker på et objekt. Kilde: Kiwakwok på engelsk Wikipedia [Public Domain]

Løste øvelser

-Oppgave 1

Finn verdien av k slik at følgende vektorer er koplaner:

Kan tjene deg: Carnot Machine

eller =

v =

W =

Løsning

Siden komponentene i vektorene er hatt, brukes derfor kriteriene for det blandede produktet:

eller · (v x W) = 0

Den løses først v x W. Vektorene vil bli uttrykt i form av enhetsvektorene Yo, J og k som skiller de tre vinkelrett retningene i rommet (bred, høy og dybde):

v= 4 Yo + J + 0 k

W= -1 Yo + 2J -1 k

v x W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x j) - 2 (J x k) = 8 k + 4 J + k -2 i = -2 Yo + 4 J + 9 k

Skalarproduktet er nå foreslått mellom U og vektoren som har resultater fra forrige operasjon, samsvarende operasjon til 0:

eller · (v x W) = (-3 Yo + k J + 2 k) · (-2 Yo + 4 J + 9 k) = 6 + 4k +18 = 0

24 + 4k = 0

Den etterspurte verdien er: k = - 6

Slik at vektoren eller er:

eller =

-Trening 2

Figuren viser et objekt hvis vekt er W = 600 N, henger i balanse takket være kablene plassert i henhold til vinklene vist i figur 3. Er det mulig å anvende Lamys teorem i denne situasjonen? I alle fall finn størrelsene på T₁, T₂ og T₃ som gjør balanse mulig.

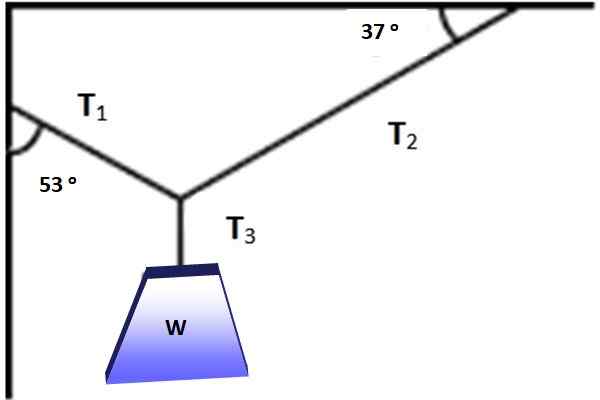Figur 3. En vekt henger i likevekt under virkningen av de tre viste spenningene. Kilde: Selvlaget.

Løsning

Lamys teorem er anvendelig i denne situasjonen hvis knuten som de tre spenningene blir brukt på, blir vurdert, siden de utgjør et system med koplanære krefter. Først er det frie kroppsdiagrammet laget for anhengsvekten, for å bestemme størrelsen på t_3:

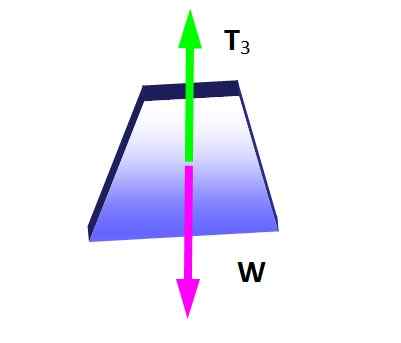Figur 4. Gratis kroppsdiagram for vekten hengende. Kilde: Selvlaget.

Fra likevektstilstanden følger det at:

Kan tjene deg: Diffraksjon av lyd: Hva er, eksempler, applikasjoner

T₃  = W = 600 n

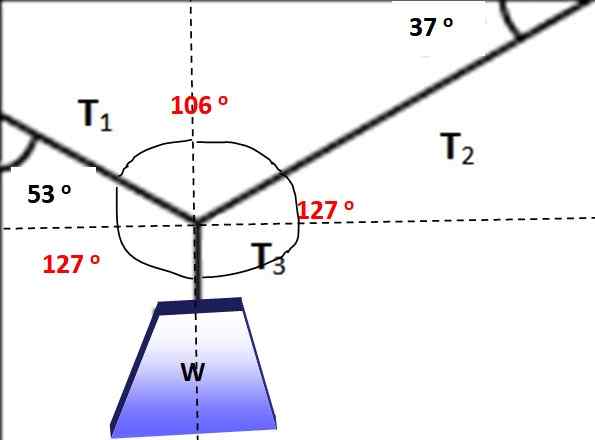
Vinklene mellom kreftene er markert i rødt i den følgende figuren, det kan lett verifiseres at summen er 360 °. Det er nå mulig å anvende Lamys teorem, siden en av styrkene og de tre vinklene mellom dem er kjent:

Figur 5.- I røde vinklene for å bruke Lamys teorem. Kilde: Selvlaget.

T₁ / SEN 127º = W / SEN 106º

Derfor: t₁ = Sen 127º (W /Sen 106º) = 498.5 n

Igjen blir Lamys teorem brukt for å fjerne t₂:

T₂ / sin 127 = t₁ / SEN 127º

T₂ = T₁ = 498.5 n

Referanser

1. Figueroa, d. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. 31-68.
2. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Editorial Company.28-66.
4. McLean, w. Schaum -serien. Mekanikk for ingeniører: statisk og dynamisk. 3. utgave. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Gjenopprettet fra: det er.Wikipedia.org.