Koniske seksjoner typer, applikasjoner, eksempler

De koniske seksjoner De er kurvene som oppnås ved å avskjære et fly med en kjegle. Det er flere måter å gjøre dette på; For eksempel, hvis flyet føres vinkelrett på kjeglenes aksiale akser, oppnås en omkrets en omkrets.

Å vippe flyet litt med hensyn til kjeglenes aksiale akser en ellipse oppnås, en kurve som er lukket, men hvis vi henter den enda mer en parabola eller en hyperbola oppnås, som det kan sees i animasjonen i figur 1.

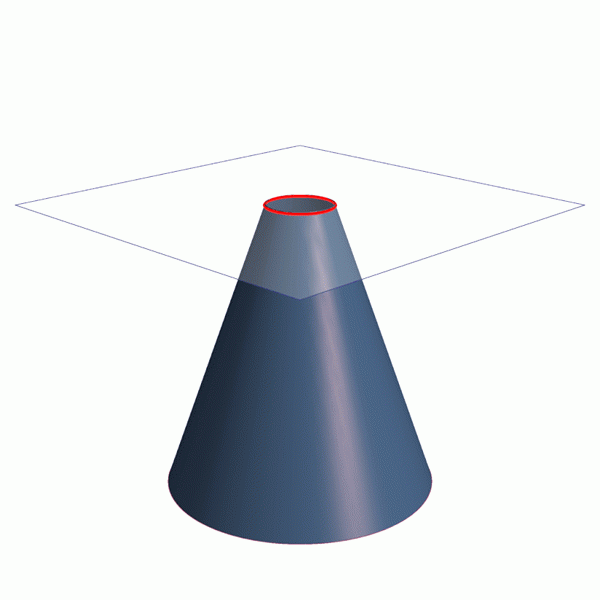Animasjon som viser hvordan du får de fire koniske seksjonene: omkrets, lignelse og hyperbola ellipse. Kilde: Wikimedia Commons. Linjer / CC0

De koniske seksjonene er en del av naturen og verden rundt oss. Ingeniørfag, arkitektur og astronomi er viktige kunnskapsgrener som bruker CONICS.

[TOC]

Betingelser for koniske seksjoner

De koniske seksjonene er definert som geometriske steder som tilfredsstiller følgende forhold:

Lignelse

Det er det geometriske stedet for alle punkter som ligger i et ekvidistant plan til et fast punkt som kalles fokus F og en rett linje også fast, kalt direktiv.

Ellipse

Et planpunkt tilhører en ellipse hvis summen av avstandene mellom det punktet og to andre faste punkter, kalt Focos og ligger på Major Axis av ellipsen, forblir konstant.

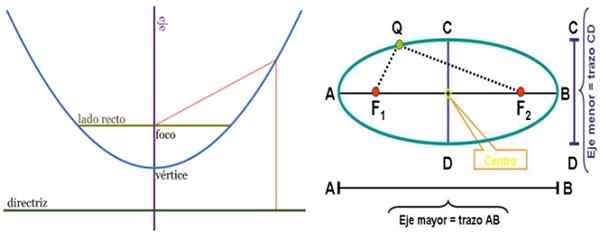Lignelsen til venstre og ellipsen til høyre, med sine respektive elementer. Fociene er poeng med mange applikasjoner. Kilde: Wikimedia Commons.

Omkrets

Det er det geometriske stedet for alle punktene som opprettholder samme avstand til et annet punkt som heter Centro. Denne avstanden er den radio av omkretsen.

Kan tjene deg: Euklidiansk avstand: konsept, formel, beregning, eksempel

Hyperbola

Sett med punkter i flyet slik at forskjellen mellom dets avstand til to faste punkter kalt Focos, det er konstant.

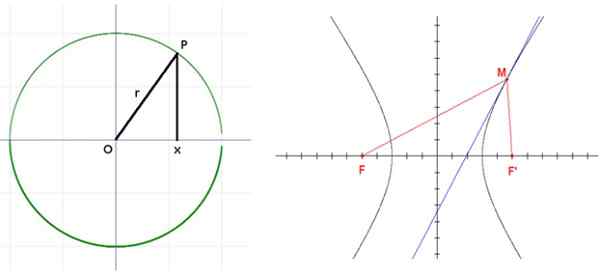Hyperbola med foci f og f. Kilde: Wikimedia Commons.

applikasjoner

La oss se på noen av de koniske seksjonsapplikasjonene:

Lignelser  

-Når et objekt lanseres, har banen som følger en lignelsesform.

-Lignelsene har bemerkelsesverdige ingeniørapplikasjoner, for eksempel i de suspenderte broene kablene skynder seg i form av lignelser.

-Lignelsene er også gode å lage reflekser og teleskoper. Dette er takket være en interessant egenskap: Når du plasserer en armatur i fokus for en parabolsk tverrgående seksjonsoverflate, vil lyset bevege seg parallelle stråler til lignalaksen.

-Hvis de lysende strålene parallelt med symmetriaksen nærmer seg den parabolske overflaten, konsentrerer den dem i fokus, en omstendighet som brukes til å lage reflektor -teleskoper, for eksempel Hale de Monte Palomar -teleskopet.

Ellipser

-Planetene til solsystemet beveger seg etter elliptiske baner, ganske nær omkretsen i tilfelle av de store planetene, inkludert landet. Solen er ikke i sentrum, men i en av søkelysene.

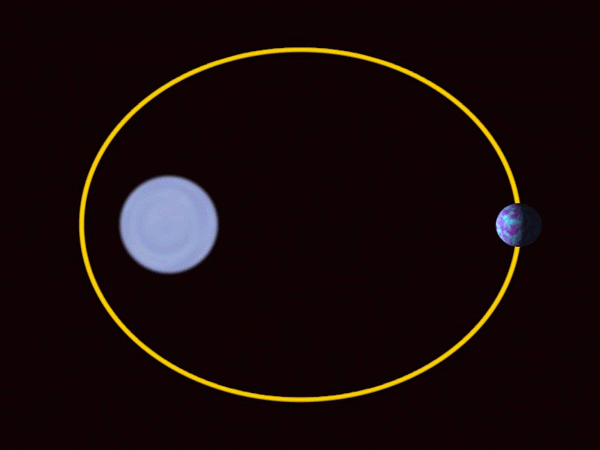Planetene til solsystemet beveger seg i elliptiske baner med solen i et av søkelysene. Kilde: Wikimedia Commons.

-Ellipsen er mye brukt i arkitektur som et dekorativt og designelement.

-Ved å plassere en reflektor i en av søkelysene i en ellipse, gjenspeiles lyset mot det andre fokuset. Det samme skjer med lyd. Det er grunnen til at i Ellipse -formede haller, som snakker stille å være lokalisert i ett fokus, blir tydelig hørt av lyttere som ligger i det andre fokuset.

Det kan tjene deg: hepagonal prisme

-Den samme egenskapen har en overraskende applikasjon innen medisinens felt. Nyneberegninger kan ødelegges av lyd. Ultralydbølger med stor intensitet genereres i en av fokusene til et elliptisk kar fullt av vann, og pasienten er lokalisert i det andre fokuset. Lydbølger påvirker og reflekterer i beregningen, og med deres energi fragmenterer de den i små biter, som personen deretter lett utviser seg under vannlating.

Hyperbolas

-Noen kometer i solsystemet følger hyperbolske baner, alltid med solen i en av fokusene.

-Hyperbolas -fokus er også veldig interessante å studere fenomenene med bølgefleksjon. For eksempel, ved å lede en lysstråle til et parabolsk speil, gjenspeiles det for eksempel i det andre fokuset, en veldig nyttig egenskap for å bygge teleskoper, siden lyset kan fokusere på et parabolsk speil og bli omdirigert til et annet mer passende sted I følge design.

-Kjøletårnene til atomkraftverk har hyperbolasformet silhuett.

-Før bruk av GPS ble hyperbolas brukt i navigasjon for å finne båter. Skipene førte om styresignaler utstedt samtidig av radio A- og B -stasjonene, og en datamaskin var ansvarlig for å registrere forskjellene i ankomsttidene for signalene, for å transformere dem til forskjeller i avstander av avstander. På denne måten ligger skipet i grenen av en hyperbola.

Prosedyren gjentas med to andre radio C- og D -stasjoner, som plasserer skipet i grenen av Nok en hyperbola. Den endelige posisjonen til båten er skjæringspunktet mellom begge hyperbolene.

Kan tjene deg: Voksende funksjon: Hvordan identifisere den, eksempler, øvelser

Omkretser

-Hjulets ankomst endret historiens gang.

-Den sirkulære bevegelsen er veldig vanlig, mange stykker dreier seg om å gi forskjellige effekter, fra fabrikker til fans.

-Selv om banene til de viktigste planetene er elliptiske, er de sirkulære banene gode tilnærminger i mange tilfeller.

-Kretser er hyppige elementer innen arkitektur, design, prosjektering og konstruksjon. Listen over sirkulære eller diskformer er uendelig: mynter, CD -er, klokker og mer.

Eksempler

Så er det to kjellere i flyet, en sirkel og en ellipse.

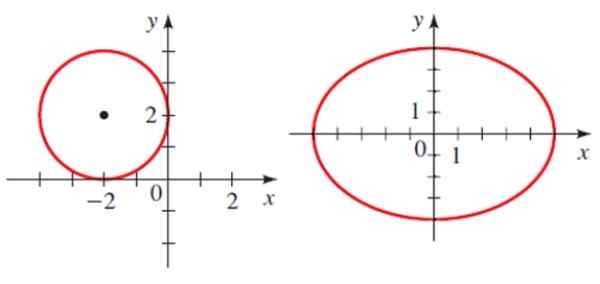Eksempler på koniske seksjoner: en sirkel og en ellipse. Kilde: Stewart, J. Forkalkning.

Hver har en analytisk ligning:

Omkrets

(X-H)² + (Y-k)² = R²

Hvor H og K er koordinatene til sentrum og R er radioen. For omkretsen vist på figuren er ligningen:

(x+2)² + (Y-2)² = 4

Ellipse

Ellipse -ligningen hvis sentrum er koordinatpunktet (h, k):

[(X-h)² /til² ]+ [(y-k)² /b² ] = 1

Hvor a og b er semi -pilene til ellipsen. For den viste ellipsen er senteret på punkt 0,0, den største semi -det samme er det samme, og den mindre semije er 4. Derfor er ligningen:

(x² /25)+ (og² / 16) = 1

Referanser

1. Hoffman, J. Valg av matematikkproblemer. Volum 2.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
4. Wikipedia. Konisk seksjon. Gjenopprettet fra: er.Wikipedia.org.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.