Chebyshov teorem det vil si applikasjoner og eksempler

Han Chebyshov teorem (eller ulikhet i Chebyshov) er et av de viktigste klassiske resultatene av sannsynlighetsteori. Det tillater estimering av sannsynligheten for en hendelse beskrevet i form av en tilfeldig variabel x, ved å gi oss et nivå som ikke er avhengig av fordelingen av den tilfeldige variabelen, men av variansen til x.

Teoremet kalles til ære for den russiske matematiske.

Denne ulikheten, eller de som på grunn av deres egenskaper kalles ulikheten i Chebyshov, brukes hovedsakelig til å tilnærme sannsynlighetene ved å beregne nivåer.

Hva er Chebyshovs teorem?

I studien av sannsynlighetsteorien hender det at hvis distribusjonsfunksjonen til en tilfeldig variabel x er kjent, kan den forventede verdien beregnes - eller matematisk håp og (x) - og dens varians var (x), så lenge disse beløp eksisterer. Gjensidig er imidlertid ikke nødvendigvis sant.

Det vil si å vite E (x) og var (x) kan ikke nødvendigvis oppnå distribusjonsfunksjonen til x, så mengder som p (| x |> k) for noen k> 0, er veldig vanskelige å oppnå. Men takket være Chebyshovs ulikhet er det mulig å estimere sannsynligheten for den tilfeldige variabelen.

Chebyshovs teorem forteller oss at hvis vi har en tilfeldig variabel X på et prøveområde med en sannsynlighetsfunksjon p, og hvis k> 0, så:

Kan tjene deg: Acutangle Triangle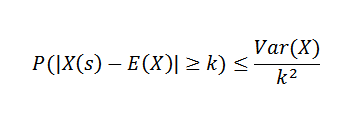

Applikasjoner og eksempler

Blant de mange applikasjonene som Chebyshovs teorem besitter, kan følgende nevnes:

1. Sannsynlighetsgrense

Dette er den vanligste applikasjonen og brukes til å gi et øvre nivå for P (| x-e (x) | ≥K) der k> 0, bare med variansen og håpet til den tilfeldige variabelen x, uten å vite sannsynlighetsfunksjonen.

Eksempel 1

Anta at antall produkter som er laget i et selskap i en uke er en tilfeldig variabel med et gjennomsnitt på 50.

Hvis det er kjent at variansen av en produksjonsuke er lik 25, hva kan vi si om sannsynligheten for at produksjonen denne uken er forskjellig med mer enn 10 til gjennomsnitt?

Løsning

Bruker Chebyshovs ulikhet vi må:

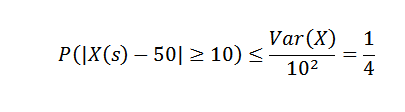
Fra dette kan vi oppnå at sannsynligheten for at antallet varer i produksjonsuken i mer enn 10 til gjennomsnittet er på det meste 1/4.

2. Demonstrasjon av grense teoremer

Chebyshovs ulikhet spiller en viktig rolle i å demonstrere de viktigste grensene teoremer. Som et eksempel har vi følgende:

Svak lov med stort antall

Denne loven slår fast at gitt en suksess x1, x2, ..., xn, ... av uavhengige tilfeldige variabler med samme gjennomsnittlig distribusjon e (xi) = μ og varians varians var (x) = σ², og et kjent gjennomsnittlig utvalg av:

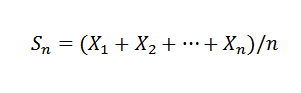
Så for K> 0 må du:

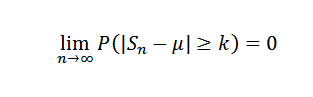
Eller tilsvarende:

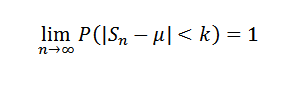
Demonstrasjon

Først merker vi følgende:

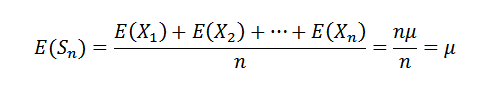
Som x1, x2, ..., er xn uavhengige, det følger at:

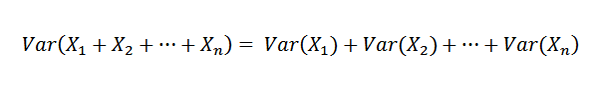
Derfor er det mulig å bekrefte følgende:

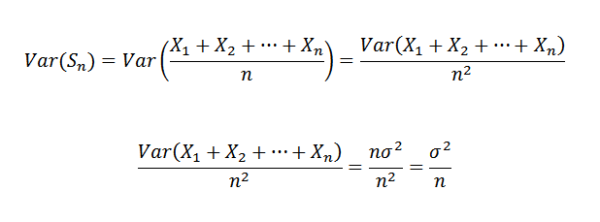
Deretter bruker du Chebyshovs teorem:

Det kan tjene deg: trigonometriske funksjoner: grunnleggende, i det kartesiske planet, eksempler, trening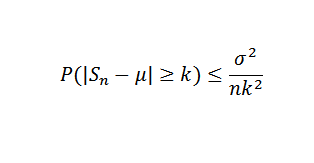

Endelig er teoremet resultat av at riktig grense er null når n har en tendens til uendelig.

Det skal bemerkes at denne testen bare ble gjort for tilfellet der det er variansen av XI; det vil si at det ikke avviker. Dermed observerer vi at teoremet alltid er sant hvis e (xi) eksisterer.

Chebyshovs grense teorem

Hvis x1, x2, ..., xn, ... er det en rekke uavhengige tilfeldige variabler slik at det er noen C0:

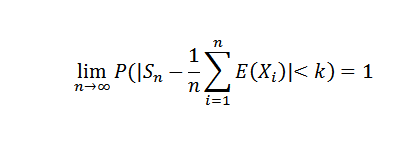
Demonstrasjon

Ettersom rekkevariets rekke. Men vi vet det:

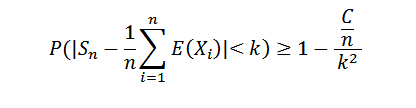
Å lage n til uendelig, det er følgende:

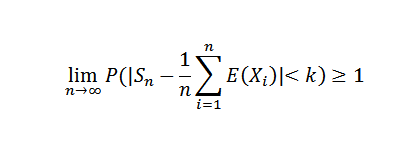
Ettersom en sannsynlighet ikke kan overstige verdien av 1, oppnås det ønskede resultatet. Som en konsekvens av dette teoremet kunne vi nevne det spesielle tilfellet med Bernoulli.

Hvis et eksperiment gjentas uavhengig av to mulige resultater (fiasko og suksess), der P er sannsynligheten for suksess i hvert eksperiment og X er den tilfeldige variabelen som representerer antall suksesser som er oppnådd, må du for hver K> 0:

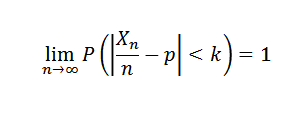
3. Prøvestørrelse

Når det gjennomsnitt.

Nettopp, det være seg x1, x2, ... xn et utvalg av uavhengige tilfeldige variabler av n størrelse og antar at e (xi) = μ og dens varians σ². Så på grunn av Chebyshovs ulikhet må du:

Kan tjene deg: Euler -nummer eller nummer E: Hvor mye OK, egenskaper, applikasjoner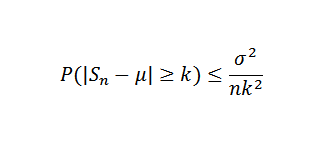

Nå være Δ> 0 fikset. Vi må:

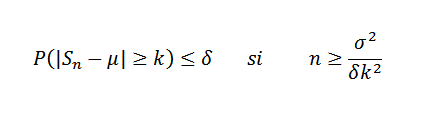
Eksempel

Anta at x1, x2, ... xn er et utvalg av uavhengige tilfeldige variabler med Bernoulli -distribusjon, slik at de tar verdi 1 med sannsynlighet P = 0.5.

Det som skal være prøvestørrelsen for å sikre at sannsynligheten for at forskjellen mellom den aritmetiske gjennomsnittlige SN og dens forventede verdi (som overstiger mer enn 0,1), er mindre enn eller lik 0.,01?

Løsning

Vi må (x) = μ = p = 0,5 og hva var (x) = σ²= P (1-P) = 0,25. For Chebyshovs ulikhet, for enhver K> 0, må vi:

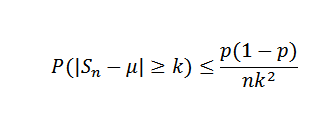
Nå, tar K = 0,1 og Δ = 0,01, må du:

På denne måten konkluderes det med at en prøvestørrelse på minst 2500 er nødvendig for å sikre at sannsynligheten for hendelsen | Sn - 0,5 |> = 0,1 er mindre enn 0,01.

Chebyshov type ulikheter

Det er forskjellige ulikheter relatert til ulikheten i Chebyshov. En av de mest kjente er Markovs ulikhet:

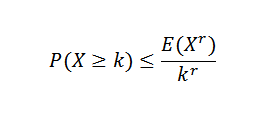
I dette uttrykket x er det en ikke -negativ tilfeldig variabel med k, r> 0.

Markovs ulikhet kan ta forskjellige former. For eksempel enten og en ikke -negativ tilfeldig variabel (så p (y> = 0) = 1) og anta at e (y) = μ eksisterer. Anta også at (e (y))^r= μ_r Det er for noen heltall r> 1. Så:

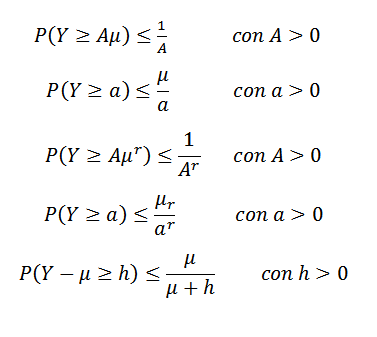
En annen ulikhet er Gauss, som forteller oss at gitt en unimodal x tilfeldig variabel med mote på null, deretter for k> 0,