Grønn teorem, demonstrasjon, applikasjoner og øvelser

Han Grønt teorem Det er en beregningsmetode som brukes til å relatere linjeintegraler med dobbeltareal eller overflateintegraler. Funksjonene som er involvert må betegnes som vektor og definerte felt innenfor bane C.

For eksempel kan et uttrykk for integrert linje være veldig komplisert å løse; I implementering av Green's teorem blir imidlertid doble integraler ganske grunnleggende. Det er alltid viktig å respektere den positive følelsen av banen, dette refererer til retning av klokken nåler.

Greens teorem er et spesielt tilfelle av Stokes 'teorem, der projeksjonen av vektorfunksjonen utføres i XY -planet.

[TOC]

Definisjon

Grønns uttrykk for Greens teorem er som følger:

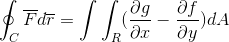
I den første termen observeres linjen integral definert av bane "c", av produktskalaren mellom vektorfunksjonen "f" og den til vektoren "r".

C: Det er den definerte banen som vektorfunksjonen vil bli projisert så lenge den er definert for det planet.

F: Vektorfunksjon, der hver av komponentene er definert av en funksjon som sådan (F, G).

A: Det er en vektor tangent til R -regionen som integralen er definert. I dette tilfellet drives det med en differensial av denne vektoren.

I det andre termen ser vi Green utviklet teorem, der det doble integralet som er definert i region R av forskjellen mellom delvise derivater av G og F, blir observert, med hensyn til x og og og og henholdsvis. For et områdeforskjell som ikke er noe mer enn produktet av begge to -dimensjonale differensialer (DX.dy).

Dette teoremet er perfekt aktuelt for rom- og overflateintegraler.

Demonstrasjon

For å demonstrere Greens teorem på en enkel måte, vil denne oppgaven bli delt opp i 2 deler. Først vil vi anta at vektor F -funksjonen bare har en definisjon i versoren Yo. Mens “G” -funksjonen tilsvarer versoren J vil være lik null.

Kan tjene deg: hvor mange hundrelapper som passer i en tiende? (Eksempler)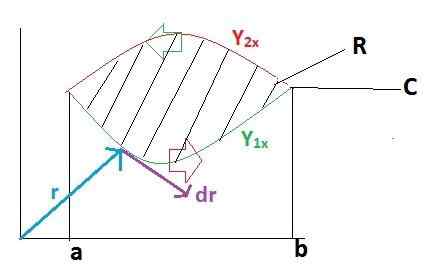Forfatter

F = f (x, y)Yo + G (x, y)J = f (x, y)Yo + 0

R = xYo + ogJ

Dr = dxYo + DyJ

Først utvikler vi linjen integral over bane C, som banen har blitt sektorisert i 2 seksjoner som går først fra A til B og etter B til A.

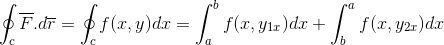
Definisjonen av det grunnleggende teoremet for beregningen for et definert integral brukes.

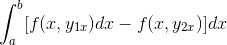
Uttrykket omorganiseres i et enkelt integral, blir gjort felles for det negative, og rekkefølgen på faktorene blir reversert.

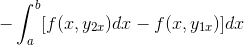
Ved å observere i detalj dette uttrykket, blir det tydelig at når du bruker kriteriene for primitiv funksjon, er det i nærvær av integralen av uttrykket avledet fra F med hensyn til og. Evaluert i parametere

[og_1x , og_2x]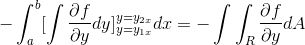

Nå er det nok å anta at Vector Fun -funksjonen bare er definert for G (x, y)J. Når når den opererer på en måte homologert til forrige sak, oppnås det:

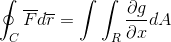
Til slutt blir de to demonstrasjonene tatt og blir med i saken der vektorfunksjonen tar verdier for begge versorene. På denne måten vises det som linjen integrert etter å ha definert og blitt betraktet som en endimensjonal bane, kan den utvikles fullt ut for flyet og rommet.

F = f (x, y)Yo + G (x, y)J

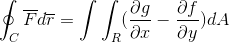
På denne måten demonstreres Greens teorem.

applikasjoner

Grønne teoremapplikasjoner er brede i filialene til fysikk og matematikk. Disse strekker seg til enhver applikasjon eller bruk som kan gis til linjeintegrasjon.

Det mekaniske arbeidet utført av en styrke F gjennom en bane C, kan utvikles av en linjeintegrert som uttrykkes som et dobbelt integral av et område gjennom Greens teorem.

Kan tjene deg: femkantet prisme: egenskaper, deler, hjørner, kanter, volum

Treghetens øyeblikk av mange kropper som er utsatt for ytre krefter på forskjellige anvendelsespunkter, reagerer også på utviklede integraler med Greens teorem.

Dette har flere funksjonaliteter i resistensstudier av materialer som er under bruk. Der eksterne verdier kan kvantifiseres og tas i betraktning før utdyping av forskjellige elementer.

Generelt letter Greens teorem forståelsen og definisjonen av områder der vektorfunksjoner er definert med hensyn til et område i henhold til en bane.

Historie

Det ble utgitt i 1828 i arbeidet Matematisk analyse av teorier om elektrisitet og magnetisme, Skrevet av den britiske matematikeren George Green. Den utforsker ganske avgjørende seksjoner i anvendelsen av beregning i fysikk, for eksempel potensialbegrepet, funksjonene til grønt og anvendelser av dets autoteorem med tittelen.

George Green formaliserte sin studentkarriere i en alder av 40 år, så langt et helt selvløst matematiker vesen. Etter å ha studert ved University of Cambridge, fortsetter forskningen hans, og gir bidrag innen akustikk, optikk og hydrodynamikk som fremdeles er i kraft i dag.

Forhold til andre teoremer

Greens teorem er en spesiell sak, og oppstår fra 2 andre veldig viktige teorier i beregningsgrenen. Dette er Kelvin-Stokes 'teorem og divergens eller Gausski-teorem.

Med utgangspunkt i noen av begge teoremene kan du nå Greens teorem. Visse definisjoner og proposisjoner er nødvendige for å utvikle disse demonstrasjonene.

Øvelser

- Følgende øvelse viser hvordan du kan transformere en linje integrert til en dobbel integral med hensyn til en region R.

Det opprinnelige uttrykket er som følger:

Kan tjene deg: hvor mye er x verdt?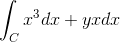

Og må evalueres i det trekantede området som sammenføyer punktene (0, 0), (1, 0), (0, 1) betegnet med C. For dette tilfellet vil den positive følelsen av svingen bli vurdert.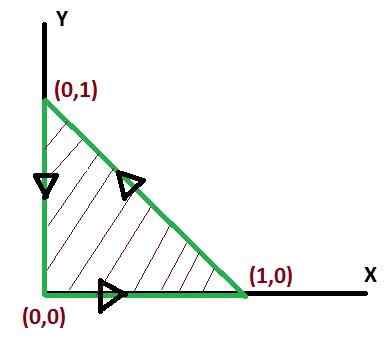

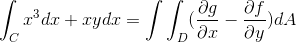
Der funksjonene som tilsvarer F og G er hentet fra

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Det er viktig å definere funksjonene som utgjør grensene for region C, for å kunne sette sammen differensialproduktet som vil dekke regionen fullstendig.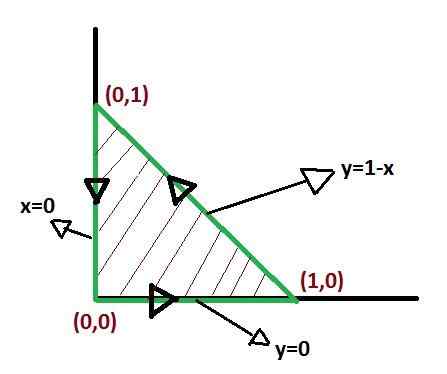

Det er ingen unik måte å definere integrasjonsgrenser når du bruker Greens teorem. Men det er former der integraler etter å ha blitt definert kan være enklere. På en slik måte at optimalisering av integrasjonsgrenser fortjener oppmerksomhet.

For dette tilfellet vurderes dette uttrykket: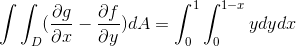

Hvor når vi løser integralene får vi:

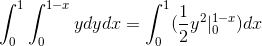
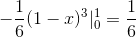
Denne verdien tilsvarer i kubiske enheter til regionen under vektorfunksjonen og på det trekantede området definert av C.

Når det. Det vil si å lage 3 parameteriserte integraler for oppløsning. Dette er tilstrekkelig bevis på effektiviteten som Robert Green bidro med hans teorem til beregningen.

Referanser

1. Introduksjon til kontinuerlig mekanikk. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. juli. 2009
2. Multivariabel kalkulus. James Stewart. Cengage Learning, 22. mars. 2011
3. En uformell historie om Green's teorem og tilhørende ideer. James Joseph Cross. Department of Mathematics, University of Melbourne, 1975
4. Varmeatferd ved bruk av greenfunksjoner. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor & Francis, 16. juli. 2010
5. Anvendelse av Green's teorem på ekstremisering av lineære integraler. Defense Technical Information Center, 1961