Tetradecágono

Hva er en tetradecágono?

Tetradecágono er en flat og lukket geometrisk figur på 14 sider, som tilhører Polygons -familien. Det er også kjent under navnet til Tetrakaidcágono, Alle ord hentet fra greske ord: "Tetra" (Cuatri), "Kai" (mer), "forfall" (ti) og "gon" (vinkel), siden den også har 14 indre vinkler.

Figuren viser en vanlig tetradagon, det vil si en hvis sider og indre vinkler alle har samme tiltak, og viser hovedegenskapene til denne figuren.

Figur 1.- Vanlig tetrade med hovedegenskapene. Kilde: f. Zapata.

Tetradecágono -elementer

• Sider: De kalles de 14 linjesegmentene som er lukket for å danne figuren. De kan alle ha samme lengde, i hvilket tilfelle polygonen er regelmessig, eller de kan være annerledes og så er det en uregelmessig tetrade.
• Hjørner: De er skjæringspunktene mellom påfølgende segmenter og tetradecágono har 14 hjørner.
• Senter: Tilsvarende punkt i toppunktene.
• Radio: segment som forener senteret med et toppunkt.
• Indre vinkel: Det er dannet av innsiden av figuren og mellom to påfølgende eller tilstøtende segmenter. Tiltak 154.286º for den vanlige tetradecágon, uavhengig av siden på siden.
• Ekstern vinkel: dannet mellom den ene siden og forlengelsen av en av de tilstøtende sidene. Uansett sidelengde måler denne vinkelen 25.7143º for en vanlig tetrade.
• Sentral vinkel: Den som har sin toppunkt sammenfallende med sentrum av polygonen og sidene er to påfølgende radioer.
• Diagonal: segment som forbinder to ikke -samtykke vertikaler.

Hvordan er en tetradecágono?

De vanlige polygonene fra N -sider som er bygget med regel og kompass har en n av skjemaet 2^r p₁... s_k, å være s_Yo Fermat Primo tall annerledes, og på sin side Fermats primtall tar form 2ⁿ + 1.

Kan tjene deg: i påvente av en linje: formel og ligninger, representasjon, eksempler

Tetradecágono har n = 14 sider, men 14 = 7 × 2, som ikke er Fermat Cousins, fordi de ikke kan uttrykkes på den angitte måten. Derfor innrømmer ikke denne polygonen nøyaktig konstruksjon med regel og kompass, men en konstruksjon som nærmer seg veldig godt, gjennom flere metoder.

Generell metode for å bygge vanlige polygoner

Følgende er en generell metode (ikke den eneste) som bygger vanlige polygoner registrert i en omkrets, inkludert den vanlige tetrade.

Den består av å dele den vertikale diameteren til denne omkretsen i så mange like deler som sider har polygon å trekke. Når det gjelder tetradecágono, vil de være de 14 delene som er nummerert i bilde 2. Dette er trinnene:

• Tegn en vertikal diameter fra A til B.
• Tegn deretter en semi -rett fra punkt A, åpne kompasset med vilkårlig åpning og gjør 14 like fordelt divisjoner om det. Semirrekt og dens divisjoner kan komme ut av omkretsen.
• Bli med på 14VA -merket (i blått på bildet) på slutten av semi -rett med punkt B.
• For å fortsette å bli med resten av merkene i semi -recreational med de respektive punktene på den vertikale diameteren (grønne punkter).
• Med spissen av kompasset i A og åpning lik målet på omkretsens diameter trekkes en lysbue. Med samme mål, men å støtte spissen i B (punkt 14 i figur 2) er en annen bue tegnet, som er kuttet med den første på punktene V og V 'indikert.

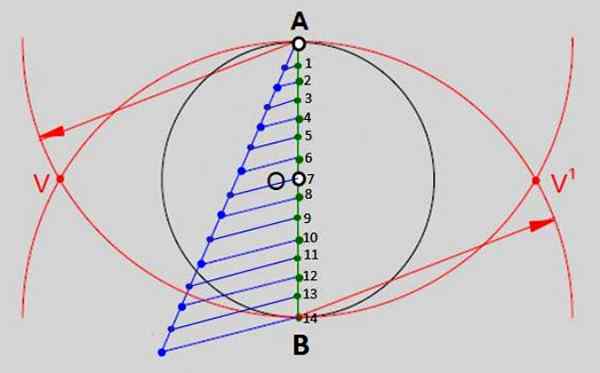Figur 2.- En av de generelle metodene for å bygge vanlige polygoner er å dele diameteren på omkretsen i så mange like deler som sider har polygon. Når det gjelder vanlig tetradech, er det 14 like deler. Kilde: f. Zapata.

• Nå, med regelen, tegner du en linje fra V 'til punkt 2 og forlenger den for å krysse omkretsen ved punkt C i figur 3. Merk kryssingspunktet, som vil være en av toppunktene på figuren.

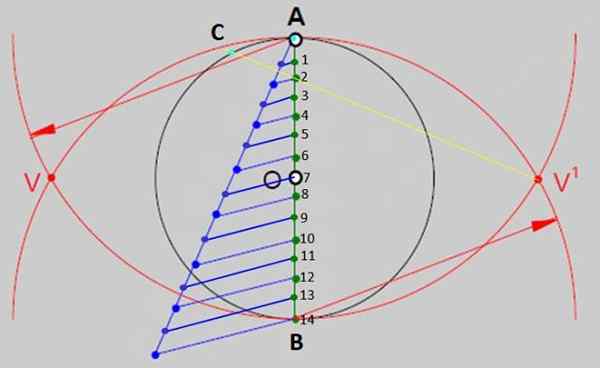Kan tjene deg: Statistikk filialer Figur 3.- AC -segmentet er målet på sidene av den bygde tetradecion. Kilde: f. Zapata.

• Åpne kompasset i vekselstrømavstanden og støtte spissen i A eller C, og tegner buer med like mål over hele omkretsen, på denne måten er den delt inn i omtrent like store deler, skjæringspunktene mellom buene og omkretsen er toppunktene er de hjørner til tetradecágono.
• Med en regel, bli med i toppunktene med linjesegmenter, og danner sidene av polygonen.
• Slett hjelpekonstruksjoner forsiktig.

I den følgende animasjonen vises en omtrentlig metode, med regel og kompass:

Figur 4.- Animasjon som viser hvordan en tetradecágon er laget (omtrent vanlig polygon). Kilde: Wikimedia Commons.

Formler for vanlig tetrade

Følgende formler er gyldige for vanlige polygoner:

• Arknummer: n
• Sidemål: a
• Apothem: l_TIL
• Radio: r
• Omkrets: s
• Område: a
• Intern vinkel: Jeg
• Ekstern vinkel: e
• Diagonal: d

Kjent side til apothem

A = 2l_TIL × tg (π/n)

For n = 14:

A = 2l_TIL × tg (π/14)

Kjent side radioen

A = 2r × sen (π/n)

Ja n = 14:

A = 2r × sen (π/14)

Kjent omkrets siden

Omkretsen er summen av sidene. Når tetradecágono er regelmessig:

P = n⋅a = 14⋅a

Hvis tetradecágono er uregelmessig, må alle sidene tilsettes direkte for å oppnå omkretsen.

Kjent område siden

A = ¼ na² × barneseng (π/n)

For n = 14:

A = ¼ (14²) × barneseng (π/14) = (7/2) a² × barneseng (π/14)

Kjent område

A = n⋅l_TIL ² × tg (π/n)

Tar n = 14 resultater:

A = 14L_TIL ² × tg (π/14)

Område basert på omkretsen og apothem

A = (P × L_TIL)/2

Kan tjene deg: Bayes teorem

Indre vinkelmål

 Når n = 14, måler den indre vinkelen til tetradecágono i grader:

I = 12 × 180º /14 = 154.286º

Måling av ekstern vinkel

E = 360º/n

Når n = 14 har du:

E = 25.7143º

Diagonaler

Formelen for beregning av antall diagonaler som er til stede i en hvilken som helst polygon, regelmessig eller ikke, er:

For n = 14:

D = 14 × 11/2 = 77 diagonaler

Eksempler

Et annet eksempel på tetradecágon

Vanlige polygoner vises gjentatte ganger i mange design, for eksempel valutaer. Når det.

Konkav og konvekse tetradecágonos

Generelt kan polygoner som tetradecágono være konveks eller konkav, i det første tilfellet overstiger målet på deres indre vinkler ikke 180º. Den vanlige tetradech er konveks, som enhver vanlig polygon, siden noen av dens indre vinkler måler 154.286º.

På den annen side, i den konkave Tetradech, måler en eller flere av de indre vinkler mer enn 180º.

Numerisk eksempel

Gitt en vanlig tetradagon hvis side måler 5 cm, finn:

a) Omkrets
b) Apotheme måling
c) Radiolengde
d) område

Svar

a) Ettersom det er en vanlig polygon, er omkretsen:

P = 14 × 5 cm = 70 cm.

b) Fra ligning A = 2L_TIL × tg (π/14), hvor a = 5 cm, apothem l_TIL:

L_TIL = a / [2 × tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

C) Radio R kan beregnes med A = 2R × Sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Det er flere alternativer for området, for eksempel A = (P × L_TIL)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Arturo Geometry. Generell metode for å tegne polygoner som er påmeldt omkretser. Gjenopprettet fra YouTube.com
3. Suppe kalkulator. Regelmessig polygonkalkulator. Gjenopprettet fra: Calculatorosoup.com.
4. Tegning. Vanlige polygoner. Gjenopprettet fra: tegning.com.
5. Requena, b. Konkav polygon. Gjenopprettet fra: Universoformulas.com.
6. Wikipedia. Byggbar polygon. Gjenopprettet fra: er.Wikipedia.org.