Bane og forskyvning

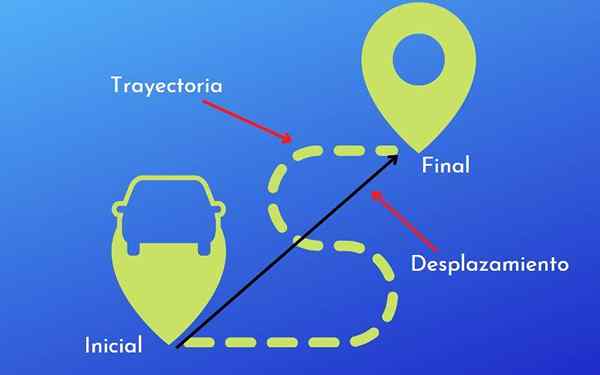
Forskjell mellom bane og forskyvning. Med lisens

De Forskjell mellom bane og forskyvning er at sistnevnte er avstanden og retningen som reiste av et objekt, mens banen er ruten eller formen som er vedtatt ved bevegelse av det objektet.

For å se tydeligere forskjellene mellom forskyvning og bane, er det imidlertid bedre å forklare gjennom eksempler som gir større forståelse av begge begrepene.

Forskyvning

Det forstås som avstanden og retningen som er reist av et objekt, under hensyntagen til dens opprinnelige posisjon og dens endelige posisjon, alltid i en rett linje. For beregningen, fordi det er en vektorstørrelse, brukes lengdemålingene kjent som centimeter, målere eller kilometer.

Formelen for beregning av forskyvning er definert som følger:

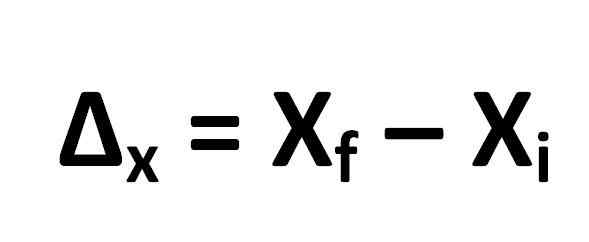
Hvorfra det følger det:

- Δ_x = Forskyvning

- X_F = endelig plassering av objektet

- X_Yo = innledende objektposisjon

Eksempel på forskyvning

1. Hvis en gruppe barn er på begynnelsen av en rute, hvis startposisjon er 50 m, beveger seg i en rett linje, og bestemmer forskyvningen i hvert av punktene x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Problemdataene blir trukket ut ved å erstatte verdiene til x₂ og x₁ I forskyvningsformelen:

- Δ_x = ?

- X_Yo = 50 m

- Δ_x = X_F - X_Yo

- Δ_x = 120 m - 50 m = 70 m

3. I denne første tilnærmingen sier vi at Δ_x Det er lik 120 m, som tilsvarer den første verdien vi finner fra x_F, mindre 50 m som er verdien av x_Yo, Det resulterer i 70 m, det vil si når man når 120 m reist, var forskyvningen 70 m til høyre.

Kan tjene deg: laboratoriegren

4. Vi fortsetter å løse på samme måte for verdiene B, C og D

- Δ_x = 90 m - 50 m = 40 m

- Δ_x = 60 m - 50 m = 10 m

- Δ_x = 40 m - 50 m = - 10 m

I dette tilfellet ga forskyvningen oss negativ, det betyr at den endelige posisjonen er i motsatt retning av startposisjonen.

Bane

Det er ruten eller linjen bestemt av et objekt under bevegelsen og den.

Den identifiseres gjennom en imaginær linje og ved å være en skalær mengde måles den i meter.

Det skal bemerkes at for å beregne banen må vi vite om kroppen er i ro eller beveger seg, det vil si at den blir sendt til referansesystemet som vi velger.

Ligningen for å beregne banen til et objekt i det internasjonale systemet er gitt av:

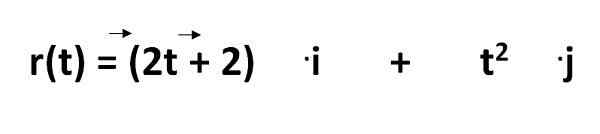
Hvorav vi må:

- R (t) = det er bane -ligningen

- 2t - 2 og t² = representerer koordinatene som en funksjon av tid

-  ^.jeg og ^.J = er enhetsvektorene

For å forstå beregningen av banen som er reist av et objekt, vil vi utvikle følgende eksempel:

Beregn ligningen på banene til følgende posisjonsvektorer:

- R (t) = (2t + 7) ^.i + t^{2 .}J

- R (t) = (t - 2) ^.FoU 2T ^.J

Første trinn: Som en bane -ligning er en funksjon av x, for at dette skal definere verdiene til henholdsvis x og y i hver av vektorene som er hevet:

1. Løs den første posisjonsvektoren:

- R (t) = (2t + 7) ^.i + t^{2 .}J

2. Ty = f (x), der x er gitt av innholdet i enhetsvektoren ^.Jeg er gitt av innholdet i enhetsvektoren ^.J:

Kan tjene deg: ad hoc: opprinnelse til begrepet, betydninger og eksempler på bruk

- X = 2t + 7

- Y = t²

3. y = f (x), det vil si at tiden ikke er en del av uttrykket, derfor må vi fjerne det, vi har:

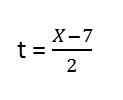
4. Vi erstatter klarering i og. Opphold:

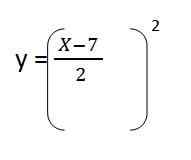
5. Vi løser innholdet i parentesen, og vi har likningen av den resulterende banen for den første enhetsvektoren:

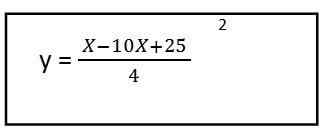
Som vi kan se, resulterte det i en andre grads ligning, dette betyr at banen er for form av en parabola.

Andre trinn: Vi fortsetter på samme måte for beregning av banen til den andre enhetsvektoren:

1. R (t) = (t - 2) ^.FoU 2T ^.J

- X = t - 2

- Y = 2t

2. Etter trinnene vi så tidligere y = f (x), må vi fjerne tiden fordi det ikke er en del av uttrykket, vi har:

- t = x + 2

3. Vi erstatter klarering i og holder oss:

- y = 2 (x + 2)

4. Løsning av parentesen har vi likningen av den resulterende banen for den andre enhetsvektoren:

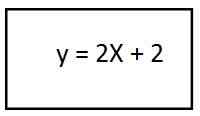
I denne prosedyren resulterte vi i en linje, som forteller oss at banen har en rettlinjet form.

Forsto begrepene forskyvning og bane kan vi utlede resten av forskjellene som eksisterer mellom begge vilkårene.

Flere forskjeller mellom forskyvning og bane

Forskyvning

- Det er avstanden og retningen som reiste av et objekt som tar hensyn til dens opprinnelige stilling og dens endelige posisjon.

- Skjer alltid i en rett linje.

- Anerkjennes med en pil.

- Bruk lengde tiltak (centimeter, meter, kilometer).

- Det er en vektormengde.

- Ta hensyn til retningen som er reist (høyre eller venstre)

- Vurderer ikke tidsbruken under turen.

Kan tjene deg: Kondensasjon: konsept, prosess, eksempler

- Det avhenger ikke av et referansesystem.

- Når utgangspunktet er det samme utgangspunktet, er forskyvningen null.

- Modulen må sammenfalle med plassen som skal turneres så lenge banen er en rett linje og det er ingen endringer i forstand å følge.

- Modulen har en tendens til å øke eller avta når bevegelsen oppstår, under hensyntagen til banen.

Bane

Det er ruten eller linjen bestemt av et objekt under bevegelsen. Adoptere geometriske former (rett, parabolsk, sirkulær eller elliptisk).

- Det er representert gjennom en tenkt linje.

- Det måles i meter.

- Det er en skalær mengde.

- Tar ikke hensyn til måten reist.

- Tenk på tiden som ble brukt under turen.

- Det avhenger av et referansesystem.

- Når utgangspunktet eller startposisjonen er den samme som den endelige posisjonen, blir banen gitt av den tilbakelagte avstanden.

- Verdien av banen sammenfaller med modulen til vektorforskyvningen, hvis den resulterende banen er en rett linje, men det er ingen endringer i forstand å følge.

- Det øker alltid når kroppen beveger seg, uavhengig av banen.

Referanser

1. Fernández, m., Fidalgo, J. (2016). Fysikk og kjemi 1. baccalaureate. Paraninfo Editions, S.TIL. Spania.
2. Guatemalan Institute of Radio Education (2011) Fundamental Physics. Første semester Zaculeu Group. Guatemala.