Trekanter historie, elementer, klassifisering, egenskaper

De trekanter De er flate og lukkede geometriske figurer, som består av tre sider. En trekant bestemmes av tre linjer som er kuttet to til to, og dannes med hverandre tre vinkler. Den trekantede formen, full av symbolikk, er til stede i utallige gjenstander og som et konstruksjonselement.

Opprinnelsen til trekanten går tapt i historien. Fra arkeologiske bevis er det kjent at primitiv menneskehet kjente ham godt, fordi arkeologiske rester bekrefter at han ble brukt i verktøy og våpen.

Figur 1. Trekanter. Kilde: Public Domain fartures.

Det er også tydelig at de gamle egypterne hadde solid kunnskap om geometri og spesielt av den trekantede formen. De ble nedfelt i de arkitektoniske elementene i sine monumentale konstruksjoner.

I Rhind Papyrus er det formler for beregning av trekanter og trapesområder, samt noen volumer og andre konsepter av rudimentær trigonometri.

På den annen side er det kjent at babylonerne var i stand til å beregne området til trekanten og andre geometriske figurer, som de brukte til praktiske formål, for eksempel divisjonene i landet. De var også klar over mange egenskaper ved trekanter.

Imidlertid var det de gamle grekerne som systematiserte mange av de hyppige geometriske konseptene i dag, selv om mye av den kunnskapen ikke var eksklusiv, siden den absolutt ble delt med disse andre gamle sivilisasjonene.

[TOC]

Elementer i trekanten

Elementene i en hvilken som helst trekant er angitt i følgende figur. Det er tre: hjørner, sider og vinkler.

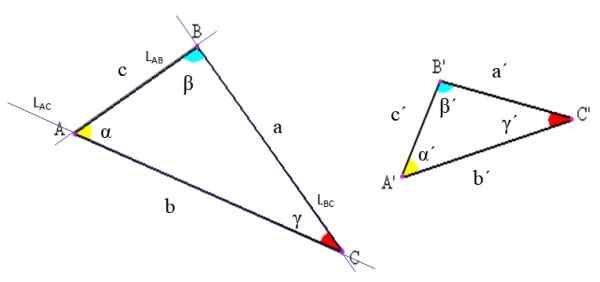Figur 2. Notasjon av trekanter og deres elementer. Kilde: Wikimedia Commons, modifisert av f. Zapata

-Hjørner: Dette er skjæringspunktene til linjene hvis segmenter bestemmer trekanten. I den øvre figuren for eksempel linjen l_Ac som inneholder vekselstrømsegmentet, krysser linjen l_AB som inneholder segment ab bare på punkt a.

-Sider: Mellom hvert par hjørner er det tegnet et linjesegment som utgjør den ene siden av trekanten. Dette segmentet kan betegnes med endene i endene eller bruke et spesifikt bokstav for å kalle det. I eksemplet på figur 2 kalles AB -siden også "C".

-Vinkler: Mellom hver side med en vanlig toppunkt har en vinkel opprinnelse, hvis toppunkt sammenfaller med trekanten. Vinkelen er vanligvis betegnet med et gresk brev, som det fremgår av begynnelsen.

For å bygge en bestemt trekant, med en gitt form og størrelse, har du bare noen av følgende datasett:

-De tre sidene, ganske åpenbare når det gjelder en trekant.

-To sider og vinkelen mellom dem, og den gjenværende siden er umiddelbart trukket.

-To vinkler (indre) og siden mellom dem. I forlengelse av de to manglende sidene er tegnet og trekanten er klar.

Notasjon

Generelt i notasjonen av trekanter brukes følgende konvensjoner: toppunktene er indikert med store bokstaver, sidene med bittesmå latinske bokstaver og vinklene med greske bokstaver (se figur 2).

På denne måten er trekanten navngitt i henhold til toppunktene. For eksempel er trekanten til venstre i figur 2 ABC -trekanten, og den til høyre er trekanten a'b'c '.

Det er også mulig å bruke andre notasjoner; For eksempel er vinkel α i figur 2 betegnet som BAC. Merk at bokstaven i toppunktet går i midten og bokstavene er skrevet i motsatt retning av klokken nåler.

Det kan tjene deg: avgrensning av problemet

Andre ganger er en circumflex -aksent plassert for å betegne vinkelen:

Eller symbolet ∠ brukes, siden den forrige notasjonen kanskje ikke er enkel på trykk, etterfulgt av bokstaven som tilsvarer toppunktet:

α = ∠A

Typer trekanter

Det er flere trekanter klassifiseringskriterier. Det mest vanlige er å klassifisere dem i henhold til målene på sidene eller i henhold til målet på deres vinkler. Avhengig av målet på sidene, kan trekantene være: skalaer, isosceles eller likestrede:

-Scalene: De tre sider er forskjellige.

-Likebent: Den har to forskjellige sider og en.

-Likesid: De tre sidene er de samme.

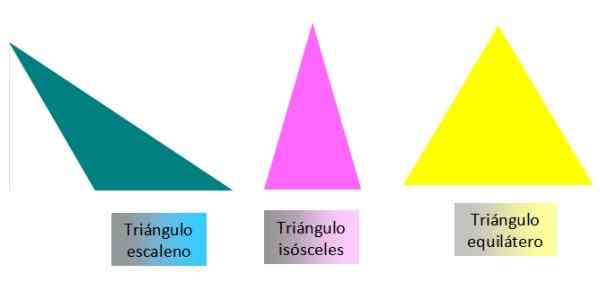Figur 3. Klassifisering av trekanter på sidene. Kilde: f. Zapata

I henhold til målet på vinklene deres, kalles trekantene slik:

-Stump, Hvis en av de indre vinklene er større enn 90º.

-Akutangel, Når de tre indre vinklene til trekanten er akutte, det vil si mindre enn 90º

-Rektangel, I tilfelle at en av sine indre vinkler er verdt 90º. Sidene som danner 90º kalles katetos og motsatt side til høyre vinkel er hypotenusen.

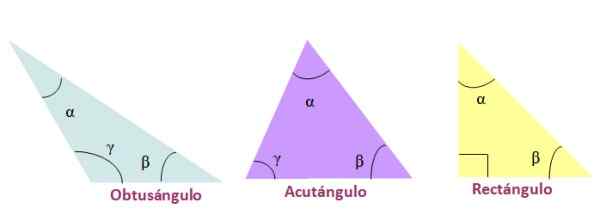Figur 4. Klassifisering av trekanter etter deres indre vinkler. Kilde: f. Zapata.

Kongruens av trekanter

Når to trekanter har samme form og har samme størrelse, sies det at de er kongruente. Selvfølgelig er kongruensen relatert til likhet, så hvorfor vi i geometri snakker om "to kongruente trekanter" i stedet for "to like trekanter"?

Vel, det er å foretrekke å bruke begrepet "kongruens" for å holde seg til sannheten, siden to trekanter kan ha samme form og størrelse, men være orientert annerledes i planet (se figur 3). Fra geometriens synspunkt ville de ikke lenger være strengt de samme.

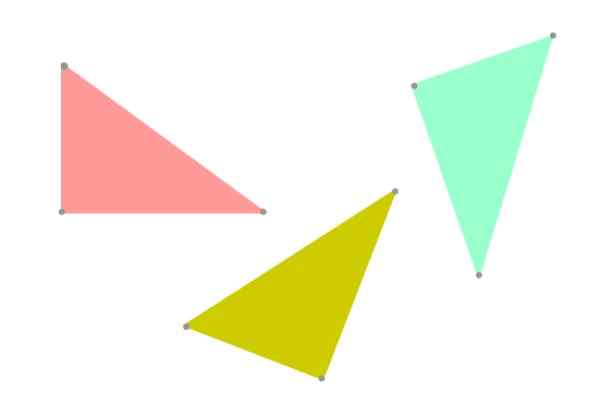Figur 5. Kongruente trekanter, men ikke nødvendigvis den samme, fordi dens orientering i flyet er annerledes. Kilde: f. Zapata.

Kongruenskriterier

To trekanter er kongruente hvis noen av følgende situasjoner oppstår:

-De tre sidene måler det samme (igjen er dette det mest åpenbare).

-De har to identiske sider og med samme vinkel mellom dem.

-Begge har to identiske indre vinkler, og siden mellom disse vinklene er den samme.

Som det kan sees, handler det om at de to trekantene oppfyller de nødvendige forholdene, slik at når de bygger dem, er deres form og størrelse nøyaktig den samme.

Kongruenskriteriene er veldig nyttige, siden utallige mekaniske deler og deler i praksis må produseres i serie, slik at deres tiltak og form er nøyaktig de samme.

Likhet mellom trekanter

En trekant ligner på en annen hvis de har samme form, selv om de er av forskjellig størrelse. For å sikre at formen er den samme, kreves det at interne vinkler har samme verdi og at sidene er proporsjonale.

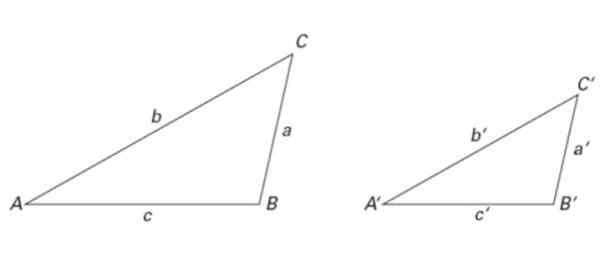Figur 6. To lignende trekanter: størrelsene deres er forskjellige, men proporsjonene deres er de samme. Kilde: f. Zapata.

Trekantene i figur 2 er også like, så vel som i figur 6. Dermed:

∠ A = ∠ A ', ∠ B = ∠ B 'og ∠ C = ∠ C '

Når det gjelder sidene, er følgende årsaker til likhet oppfylt:

a/a '= b/b' = c/c '

Egenskaper

De grunnleggende egenskapene til trekanter er som følger:

-Summen av de indre vinklene til en hvilken som helst trekant er alltid 180º.

-For enhver trekant er summen av de ytre vinklene lik 360 °.

Kan tjene deg: grunnleggende forskning: egenskaper, definisjon, eksempler

- En ytre vinkel på en trekant er lik summen av de to indre vinklene som ikke er ved siden av den vinkelen.

Teoremer

Første teorem om slikt

De tilskrives gresk filosof og matematiker Tales of Miletus, som utviklet flere teorier relatert til geometri. Den første av dem etablerer følgende:

Hvis flere parallelle linjer kutter to tverrgående linjer, bestemmer de segmenter som er proporsjonale.

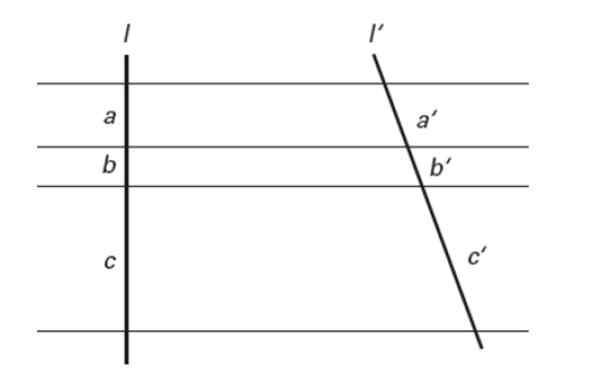Figur 7. Tales Theorem. Kilde: f. Zapata.

Med andre ord:

a/a '= b/b' = c/c '

Den første teoremet til slikt er anvendelig for en trekant, for eksempel er det ABC Blue Triangle til venstre, som er kuttet av de røde parallellene til høyre:

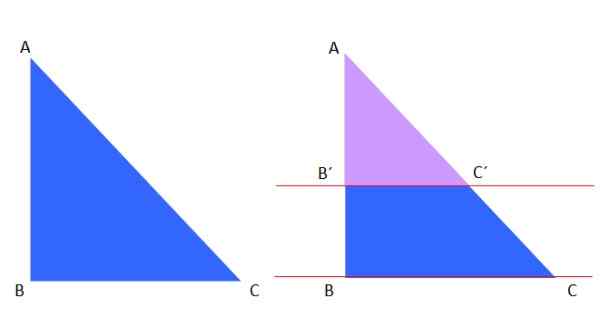Figur 8. Teoremet om slike og lignende trekanter.

Den fiolette trekanten av Violet ligner på ABC Blue Triangle, derfor kan følgende ifølge et slikt teorem skrives:

Ab '/ac' = ab/ac

Og det er i samsvar med det som ble forklart ovenfor i segmentet av trekanten likhet. Forresten kan parallelle linjer også være vertikale eller parallelle med hypotenuse og lignende trekanter oppnås.

Andre teorem om dette

Dette teoremet refererer også til en trekant og en midtkrets eller, som de som er vist nedenfor. I denne figuren er AC en diameter på omkretsen og B er et punkt i den, og er B -forskjellig fra A og B.

Den andre teoremet til slike stater at:

Vinkelen mellom AB- og BC -segmentene er alltid 90º, derfor er ABC -trekanten rektangel.

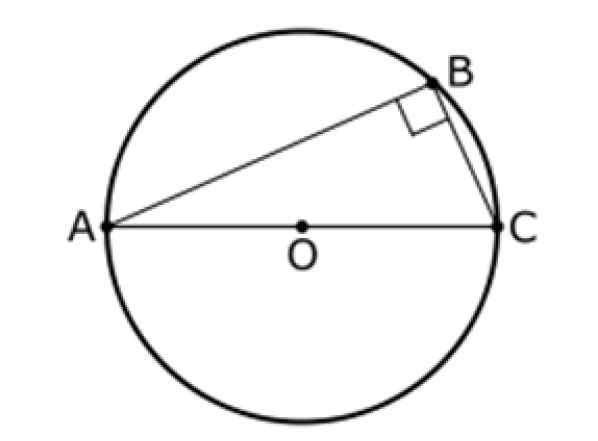Figur 9. Det andre teoremet til slikt. Kilde: Wikimedia Commons. Inductiveload [Public Domain].

Pythagoras teorem

Dette er en av de mest kjente teoremene i historien. Det skyldes den greske matematikeren Pythagoras av Samos (569 - 475 til. C.) og er gjeldende for en riktig trekant. Sier det:

Summen av rutene på lengden rektangelet Triangle -kategoriene, er lik lengden på hypotenusen høy til torget.

Hvis vi som et eksempel tar den blå trekanten i figur 8, eller den fiolette trekanten, ettersom begge er rektangler, kan det sies at:

Ac² = Ab² + BC² (Blå trekant)

Ac '² = Ab '² + BC '² (Violet trekant)

Området til en trekant

Trekantområdet er gitt av produktet av basen til og høyden h, delt med 2. Og ved trigonometri, kan denne høyden skrives som H = B sinθ.

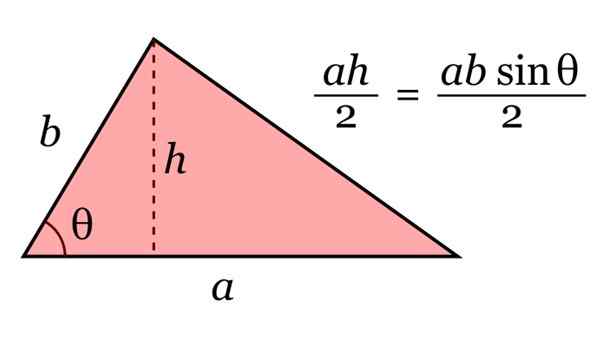Figur 10. Området til trekanten. Kilde: Wikimedia Commons.

Eksempler på trekanter

Eksempel 1

Det sies at gjennom sitt første teorem klarte slikt å måle høyden på den store pyramiden i Egypt, et av de 7 underverkene i den eldgamle verden, og målte skyggen som den projiserte på bakken og den som projiserer en stav fast i bakken.

Dette er ordningen med prosedyren etterfulgt av slikt:

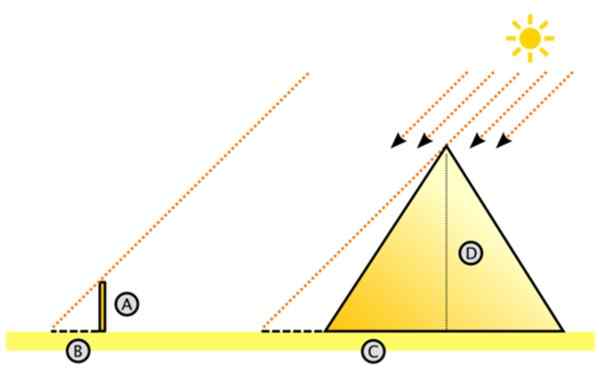Figur 11. Ordning for å måle høyden på den store pyramiden ved likhet med trekanter. Kilde: Wikimedia Commons. Dake [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Slike med rette antok at solstrålene påvirker parallellen. Med dette i bakhodet forestilte han seg den store høyre trekanten.

Det er høyden på pyramiden og C er avstanden på bakken målt fra sentrum til skyggen projisert av pyramiden på ørkenbunnen. Det kan være arbeidskrevende å måle C, men det er absolutt enklere enn å måle pyramidenens høyde.

På venstre side er den lille trekanten, fra katter A og B, hvor A er høyden på staven som sitter vertikalt på gulvet og B er skyggen den projiserer. Begge lengdene er målbare, akkurat som C (C er lik lengden på skyggen + halvparten av lengden på pyramiden).

Kan tjene deg: Hva er taktile stimuli?

Deretter, ved likhet med trekanter:

A/b = d/c

Og høyden på den store pyramiden viser seg å være: D = C.(A/B)

Eksempel 2

Civil Construction Armour er strukturer basert på rette stenger for tynn tre eller metall, som brukes som støtte i mange bygninger. De er også kjent som gitter, takstoler eller retikulert (Fagverk på engelsk).

I dem er trekantene alltid til stede, fordi stolpene er koblet sammen på punkter som kalles noder, som kan være fikset eller artikulert.

Figur 12. Trekanten er til stede i rammen av denne broen. Kilde: Pxhere.

Eksempel 3

Metoden kjent som triangulering lar deg oppnå plasseringen av utilgjengelige punkter som kjenner andre enklere avstander å måle, under forutsetning av at det dannes en trekant som inkluderer den ønskede plasseringen av den ønskede plasseringen.

For eksempel, i den følgende figuren du vil vite på hvilket tidspunkt havet er skipet, betegnet som b.

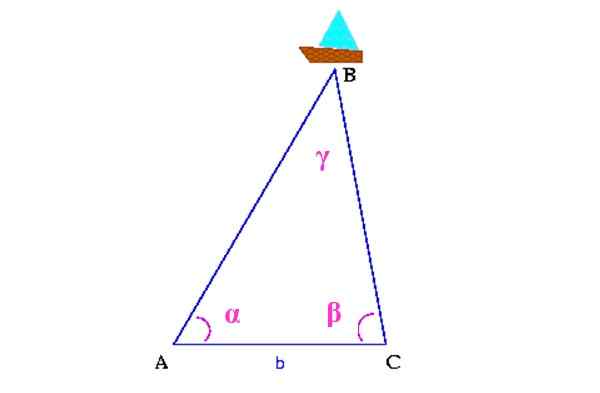Figur 13. Trianguleringsordning for å lokalisere skipet. Kilde: Wikimedia Commons. Colette [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

For det første måles avstanden mellom to punkter på kysten, som i figuren er a og c. Da må du bestemme vinklene α og β, ved hjelp av en Theodolite, En enhet som tjener til å måle vertikale og horisontale vinkler.

Med all denne informasjonen er det bygget en trekant hvis øvre toppunkt er skipet. Det ville redusere vinkelen γ, ved hjelp av måter.

Øvelser

Oppgave 1

I figuren vist er solstrålene parallelle. På denne måten projiserer det 5 -meter høye treet en 6 -meter skygge på bakken. På samme tid er skyggen av bygningen 40 meter. Etter et slikt teorem om slikt, finn høyden på bygningen.

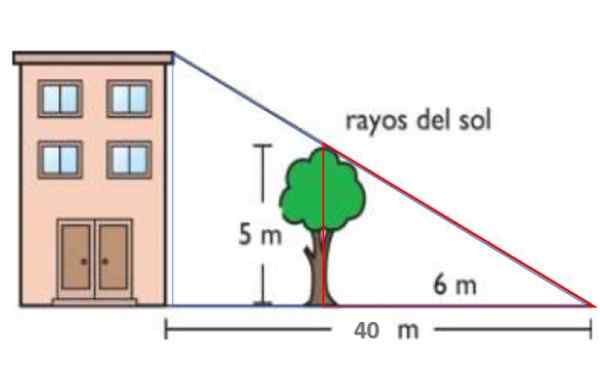Figur 14. Ordningen for året løst 1. Kilde: f. Zapata.

Løsning

Den røde trekanten har henholdsvis sider på henholdsvis 5 og 6 meter, mens den blå har en høyde H -høyden på bygningen og basen 40 meter. Begge trekantene er derfor like:

H / 40 = 5/6 → H = 40.(5/6) M = 33.3 m

Oppgave 2

Du må vite den horisontale avstanden mellom to punkter TIL og B, Men de ligger i et veldig uregelmessig terreng.

Omtrent på midtpunktet (P_m) Fra dette landet skiller en fremtredende 1.75 meter høy. Hvis målebåndet indikerer 26 meter i lengde målt fra A til prominens, og 27 meter fra B til samme punkt, finn avstanden AB.

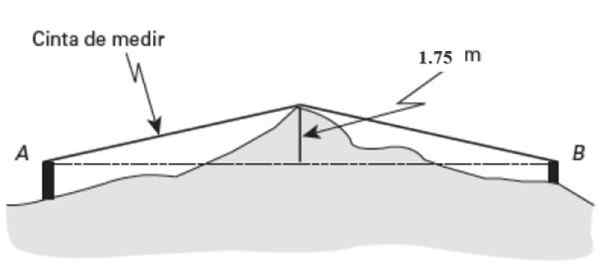Figur 15. Ordning for øvelsen løst 2. Kilde: Jiménez, R. Matematikk II. Geometri og trigonometri.

Løsning

Pythagoras -teorem brukes på en av de to rektangler -trekantene i figuren. Begynner med den til venstre:

Hypotenuse = c = 26 meter

Høyde = a = 1.75 meter

Ap_m = (26² - 1.75²)^1/2 = 25.94 m

Nå brukes Pythagoras i høyre trekant, denne gangen C = 27 meter, A = 1.75 meter. Med disse verdiene:

BP_m= (27² - 1.75²)^1/2 = 26.94 m

Avstanden AB legger til disse resultatene:

AB = 25.94 m +26.94 m = 52.88 m.

Referanser

1. Baldor, J. TIL. 1973.Flat og romgeometri. Sentralamerikansk kulturell.
2. Barredo, d. Geometrien til trekanten. Gjenopprettet fra: Ficus.pntic.Mec.er.
3. Jiménez, r. 2010. Matematikk II. Geometri og trigonometri. Andre utgave. Pearson.
4. Wentworth, g. Planetgeometri. Gjenopprettet fra: Gutenberg.org.
5. Wikipedia. Triangel. Gjenopprettet fra: er. Wikipedia.org.