Matte

Relativ verdi

Relativ verdi

Hva er den relative verdien av et tall?

Han relativ verdi av et tall o Desimalsystemsifret avhenger av posisjonen det inntar når det er en del av en figur. Derfor sies det at det er en posisjonsverdi. Et veldig enkelt eksempel: den relativ verdi på 1 I nummer 123, Det blir 100, Fordi 1 inntar hundreviss stilling.

Et annet eksempel: nummer 58 er dannet av sifre 5 og 8. Undersøkelse av dette tallet fra høyre til venstre, er den relative verdien på 8 8, for å være i enhetens plassering og den relative verdien på 5 er 50, for å okkupere titrenes sted. Antallet leses "Fifty -Eight".

På den annen side har de samme sifrene forskjellige relative verdier i nummer 85, siden de har utvekslet posisjoner. Starter fra høyre til venstre, er den relative verdien av 5 i dette tilfellet 5, den relative verdien på 8 er 80 og tallet blir lest "åtti -fem".

Hvordan finne den relative verdien til et tall?

Den generelle prosedyren for å finne den relative verdien til hvert siffer er som følger:

  • Det første sifferet fra høyre til venstre er i posisjonen til enhetene, og deres verdi multipliseres med 1.
  • Følgende siffer tilsvarer titalls og multipliseres med 10.
  • Neste stilling tilsvarer hundrevis og verdien av sifferet multipliseres med 100.
  • Neste stilling er tusen, derfor multipliseres sifferet med 1000.

Og så videre for større tall, multipliser sifret med tilsvarende 10 kraft: 100000, 100000 og utover.

For eksempel kan nummer 321 skrives som 3*100 + 2*10 + 1*1, eller tilsvarende 300 + 20 + 1. I forrige eksempel kan det raskt sees at den relative verdien på 3 er 300, 2 er 20 og 1 er 1.

Kan tjene deg: Distributive eiendommer

Eksempler på relative verdier

Nummer 727

For å bestemme den relative verdien av et siffer må du ledes av følgende grunnleggende prinsipp for den skriftlige nummereringen av desimalsystemet:

Ethvert siffer til venstre for en annen representerer en enhet 10 ganger høyere, og omvendt: hvert siffer til høyre for en annen, representerer en enhet 10 ganger mindre. 

For eksempel består 727 -figuren, som lyder "syv hundre tjue -syv", av sifre 2 og 7, med 7 gjentatte, men okkuperer forskjellige posisjoner.

Når du leser 727 fra høyre til venstre, observeres det at de 7 til høyre okkuperer enhetenes plassering, derfor multipliseres den med 1:

7 x 1 = 7

Og dens relative verdi er 7.

Siffer 2 i midten opptar tittens plassering og for å finne deres relative verdi, multipliseres det med 10:

2 x 10 = 20

Endelig på 7 til det ekstreme venstre har hundrevis posisjon. Da må du multiplisere med 100 og dens relative verdi er:

7 x 100 = 700

Merk at bare når sifferet opptar enhetenes plassering, er at dens absolutte verdi og dens relative verdi er lik. Derfor, hvis den relative verdien av antallet er VR og dens absolutte verdi er VA, er den generelle formelen for å finne den relative verdien:

VR = Absolutt verdi VA × Verdi av sin posisjon

Et tall kan skrives som summen av de relative verdiene for sifrene, dette er kjent som utviklet notasjon. Fortsetter med eksemplet på nummer 727 må du:

727 = 700 + 20 + 7

Og hvis du foretrekker å bruke kreftene på 10, er tallet 727 også uttrykt tilsvarende som:

727 = 7 ∙ 102 + 2 ∙ 101 + 7 ∙ 100

Det kan tjene deg: Multipler av 8: Hva er og forklaring

Der eksponentene for kraften basert på 10 representerer posisjonen til hvert siffer og kalles Indekser. I den følgende figuren er et annet eksempel illustrert.

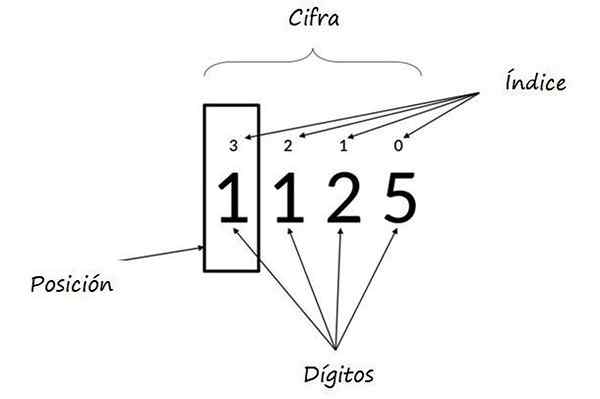I nummer 1125 er den relative verdien på 5 5, 2 er 20, 1 er 100 og venstre 1 i boksen er 1000. Kilde: Wikimedia Commons.

Nummer 63

Fra venstre til høyre er 3 i enhetens posisjon, derfor:

Relativ verdi på 3: 3 x 1 = 3

Når det gjelder 6, er dette i titallens posisjon, da:

Relativ verdi på 6: 6 x 10 = 60

Nummer 603

Dette tallet er forskjellig fra det forrige, for selv om den relative verdien på 0 er 0, har de andre sifrene forskjellige relative verdier. Starter fra høyre til venstre som alltid:

  • Relativ verdi på 3: 3 x 1 = 3
  • Relativ verdi på 0: 0 x 10 = 0
  • Relativ verdi på 6: 6 x 100 = 600

Nummer 630

I dette tilfellet er 0 i posisjonen til enhetene:

  • Relativ verdi på 0: 0 x 1 = 0
  • Relativ verdi på 3: 3 x 10 = 30
  • Relativ verdi på 6: 6 x 100 = 600

Løste øvelser

Oppgave 1

Angi den relative verdien av de understrekede tallene:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Løsning

a) Siffer 1 i 1209 inntar tusen eller tusenvis av posisjonen. Derfor er den relative verdien 1000.

VR (1) = 1 x 1000 = 1000

b) De 2 okkuperer enhetene til enhetene i 2782, derfor er dens relative verdi 2.

c) I 376 er de 7 i titallens posisjon og:

VR (7) = 7 x 10 = 70.

d) I 3045 er de 4 også i titallens posisjon:

VR (4) = 4 x 10 = 40.

e) Av 273 er ​​de 3 i stedet for enhetene, og deres relative verdi sammenfaller med figuren til sifferet, det vil si:

Kan tjene deg: sekskantet pyramide

VR (3) = 3 x 1 = 3

Oppgave 2

Skriv det laveste antallet 5 sifre, uten at noen gjentas og oppfyller følgende forhold:

a) at alle sifre er forskjellige

b) den har en 7 i tusen

c) De 8 er i enhetens posisjon.

Løsning på

Det minste 5 -sifret nummeret, med dem alle, må begynne med 1, siden selv er lavere, ettersom det første sifferet til venstre ikke teller, derfor er antallet som er søkt:

10234

Løsning b

Millarposisjonen for 7 tilsvarer 7000, men ettersom du vil ha den minste mulige figuren som inneholder 5 sifre, må antallet starte med 1, etterfulgt av 7 og deretter 023 i de gjenværende posisjonene, siden ingen siffer må gjentas.

Derfor er tallet:

17023

Løsning c

Som bedt om at de 8 skal være i enhetens posisjon, må det være ytterst til høyre. Å være det minst mulige antallet, uten at noen av de 5 sifrene som blir gjentatt, er antallet som er søkt:

10238

Øvelse 3

Beregn den absolutte og relative verdien (av hver figur) på tallet 579.

Løsning

Det har at 579 er lik 5 × 100+7 × 10+9 × 1, eller tilsvarende, den er lik 500+70+9. Derfor er den relative verdien på 5 500, den relative verdien på 7 er 70 og 9 er 9.

På den annen side er den absolutte verdien på 579 lik 579.

Oppgave 4

Gi nummer 9.648.736, hva er den relative verdien 9 og første 6 (fra venstre til høyre)? Hva er den absolutte verdien av det gitte tallet?

Løsning

Ved omskriving til nummer 9.648.736 Det oppnås at dette tilsvarer

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

eller du kan skrive som

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Slik at den relative verdien på 9 er 9.000.000 og den relative verdien av de første 6 er 600.000.

På den annen side er den absolutte verdien av det gitte tallet 9.648.736.