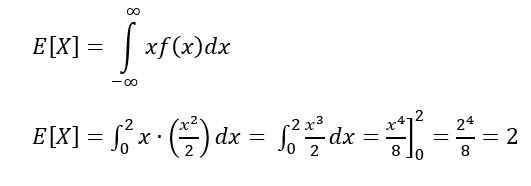Kontinuerlig tilfeldig variabel

Vi forklarer hva en kontinuerlig tilfeldig variabel, dens egenskaper, eksempler og en løst øvelse er

Hva er en kontinuerlig tilfeldig variabel?

EN Kontinuerlig tilfeldig variabel Det er en numerisk verdi oppnådd tilfeldig, som er resultatet av å gjøre et eksperiment og kan ta uendelige verdier. Dette betyr at det, kjent to påfølgende verdier av variabelen, alltid er mulig å finne en annen mellomverdi mellom dem.

Ved å ha en uendelig mengde verdier, er samlingen av kontinuerlige variable verdier ikke regnskapsført og tilhører nesten alltid settet med reelle tall.

Eksempler på denne typen variabler er statens status, vekt og kroppstemperatur, men utallige av dem kan defineres, vil flere eksempler bli funnet nedenfor. I motsetning til den kontinuerlige tilfeldige variabelen, er det den diskrete tilfeldige variabelen, som er regnskap, for eksempel antall døtre i en familie, eller hvor mange biler et byrå selger etter en måned.

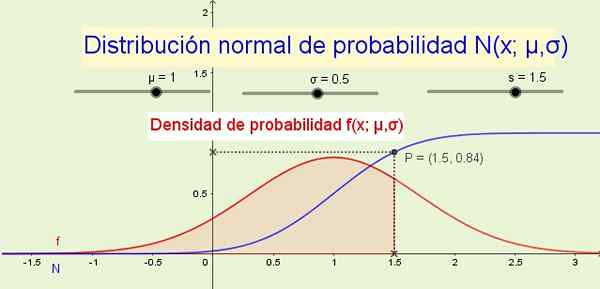
Diskrete tilfeldige variabler følger ofte normal sannsynlighetsfordeling. Kilde: f. Zapata.

En kontinuerlig tilfeldig variabel er betegnet ved hjelp av en store bokstav som X, og de uendelige verdiene som variabelen tar er de mulige resultatene av det tilfeldige eksperimentet:

X = x₁, x₂, x₃,… ∞

Hver verdi har en viss sannsynlighet for forekomst, og til modellen som denne sannsynligheten beregnes, kalles den sannsynlighetsfordeling.

Men siden x tar uendelige verdier, kan ikke sannsynligheten for spesifikke verdier av variabelen beregnes. Så det er nødvendig å definere en funksjon f (x), kalt akkumulert distribusjonsfunksjon, eller ganske enkelt distribusjonsfunksjon, i henhold til hvilken akkumulert sannsynlighet beregnes til en viss verdi eller mellom to verdier:

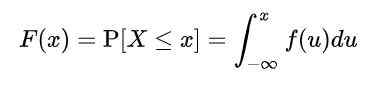
Hvor f (u) motta navnet på Tetthetsfunksjon. Definert på denne måten, F (x) representerer sannsynligheten for at X er mellom -∞ og x.

Kjennetegn på en kontinuerlig tilfeldig variabel

De kontinuerlige tilfeldige variablene er fullførte f (x).

Tetthetsfunksjonen f (x) Må oppfylle følgende egenskaper:

• Funksjonen f (x) Det er positivt: f (x)> = 0
• Området under kurven y = f (x) Det er alltid lik 1, det vil si at sannsynligheten for forekomst av et eller annet resultat x I intervallet (-∞, +∞) er 100%.
• Sannsynligheten for at x er i intervallet [a, b] beregnes med følgende definert integral:

Kan tjene deg: Curtosis: Definisjon, typer, formler, hva er det for for eksempel

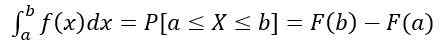
Som tilsvarer området under kurven y = f (x), forstått mellom til og b. I tillegg:

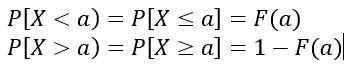
Verdiene til f (x) De representerer ikke en sannsynlighet, så P [x = c] = 0. De relevante verdiene er de som tilsvarer området under kurven y = f (x), som representerer en sannsynlighet.

• Ved å utlede distribusjonsfunksjonen F (x) med respekt for x, er oppnådd f (x).

Grafen til f (x) For en kontinuerlig tilfeldig variabel er den analog med frekvenspolygonen som er bygget for en diskret statistisk variabel, med forskjellen at for den tilfeldige variabelen blir bredden på intervallet uendeligimal.

Håp

Hope er et av de karakteristiske målene for en kontinuerlig variabel. Håpet eller forventet verdi av X Indikerer verdien som forventes å skje oftere, og beregnes gjennom følgende integral:

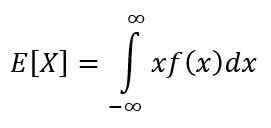
Egenskapene er:

• E [a∙ x] = a∙ E [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Hvor beløpene til og b De er reelle tall.

Eksempler

Som tidligere indikert er det mange situasjoner der en eller flere kontinuerlige tilfeldige variabler kan defineres. I vitenskap og andre områder er de vanligste av tid, lengde, vekt, volum og temperatur:

Tid

For å optimalisere prosesser og tjenester, er eksperimenter designet som studerer tiden de tar for å bli utført:

X = tid som tar en klient til bankvinduet.

Y = hva som tar et fastfood -sted i servering av en bestilling.

Z = tid der en viss kjemisk reaksjon oppstår.

Stature og vekter

I mange studier på mennesker og dyr er staturer og vekter relevante:

X = jenterhøyde på et 6. kurs. Grad på hver skole i en by.

Kan tjene deg: kongruens: kongruente figurer, kriterier, eksempler, øvelser

Y = vekt av babyer ved fødselen på et offentlig sykehus.

Z = vekten av kyrne på en gård.

Temperaturer

Temperaturen er en relevant parameter i en rekke kjemiske prosesser, som vanligvis tar uendelige verdier i et visst område:

X = temperatur som en viss kjemisk reaksjon oppstår, vel vitende om at dette skjer mellom 80 ºC og 120 ºC.

Løste øvelser

Oppgave 1

Bestem hva som er de kontinuerlige tilfeldige variablene:

1. Antall studenter som deltar på universitetets kaffe til dag.
2. Blodtrykk fra pasienter som kommer til et legevakt.
3. Lengde på fuglekvinger, av en truet art, som bor i en reserve.
4. Tid mellom en person og en annen blir behandlet i en bank.
5. Mengde mangelfulle produkter per måned på en fabrikk.
6. Kolesterolnivåer i kyllingene på en gård.
7. Mengde gatelamper i en gate, på totalt 12.

Løsning

1.- Antall studenter som er ivaretatt dagen er følelsesløs, derfor er denne variabelen ikke kontinuerlig, men diskret.

2.- Det er kontinuerlig. Blodtrykket til pasienter kan ta enhver verdi i et gitt område.

3.- Kontinuerlig variabel, siden lengden på vingen til en fugl tar enhver verdi mellom et minimum og et maksimum, avhengig av arten.

4.- Tiden mellom kundeservice er variabel og kan ta enhver verdi i et gitt område, for eksempel mellom 1 og 5 minutter.

5.- Ettersom antall mangelfulle produkter er regnskap, er det en diskret tilfeldig variabel.

6.- Denne variabelen er kontinuerlig, siden nivået av kolesterol i kyllingene tar noen verdi i et tidligere bestemt område.

Kan tjene deg: komplementære vinkler: Hvilket og hvordan de blir beregnet, eksempler, øvelser

7.- Diskret. Antall lys på belysning som fungerer er et regnskapsbeløp.

Oppgave 2

Kontinuerlig tilfeldig variabel er definert X = "kolesterolnivå " I en viss rekke kyllinger av en gård, som har følgende tetthetsfunksjon f (x):

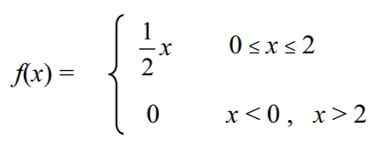
Beregn følgende:

1. F (x)
2. P [x ≤2]
3. Håpet Eks]

Løsning på

I henhold til definisjonen gitt i begynnelsen:

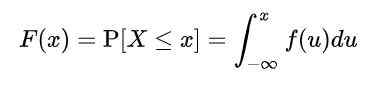
Derfor, F (x) Det er en funksjon i deler. For intervallet x<0, F (x) Det er lik 0, for egenskapene som er angitt i begynnelsen.

I intervallet 0≤x≤2, Ubestemt integrert er løst:

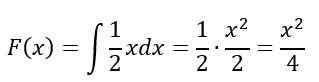
Til slutt, for intervallet x> 2, F (x) = 1, I henhold til egenskaper, derfor, F (x) Det forblir slik:

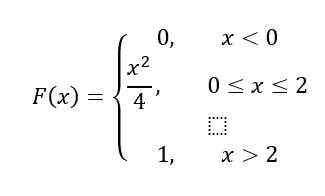
Løsning b

Den etterspurte sannsynligheten er F (1.2) og Como x = 1.2 Det er funnet mellom 0≤x≤2, den delen av F (x) Å evaluere:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Løsning c

For å beregne håpet eller forventet verdi brukes den: