Lineært variasjonskonsept, eksempler, trening løst

De Lineær variasjon Det oppstår mellom to fysiske størrelser når grafen som representerer dem er en rett linje. Det tilsvarer å bekrefte at variablene er i lineær avhengighet, slik at hvis en av dem vi kaller det "y" og den andre "x", vil de være relatert ved matematisk uttrykk:

y = mx + b

I denne formelen er M og B reelle tall. Verdien av M representerer linjens skråning eller tilbøyelighet - som alltid er konstant - og B er kuttet på linjen med den vertikale aksen.

Den lineære variasjonen av en styrke med hensyn til en annen betyr at grafen er en rett linje. Kilde: Joulesergio/CC BY-S (https: // CreativeCommons.Org/lisenser/by-SA/4.0)

Hvert fenomen som reagerer på en lineær variasjon har forskjellige navn på variablene, som vi vil se i følgende eksempler. Imidlertid er den matematiske formen for ligningen den samme.

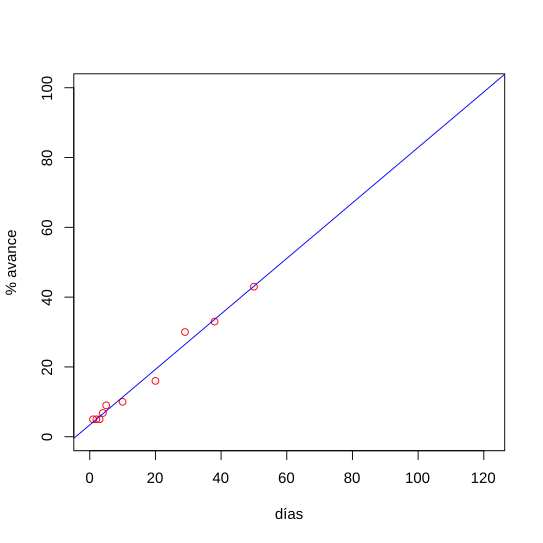
Eksperimentelt kan etableres hvis det er et lineært forhold mellom to størrelser, og måler par av verdier (x, y).

Poengene som er oppnådd er grafiske i et millimeterpapir og blir observert hvis de har en lineær trend, det vil si hvis det er en linje som tilstrekkelig tilpasser seg eksperimentelle data.

I første omgang kan denne linjen trekkes visuelt, men ved hjelp av en Lineær regresjon De kan bli funnet analytisk, verdiene til M og B på linjen som passer best for eksperimentelle punkter.

[TOC]

Eksempler på lineær variasjon

Det er mange naturfenomener, så vel som etablerte sammenhenger mellom målingsmønstre, som for eksempel overholder en lineær variasjon, for eksempel:

Hastighet i den jevnt varierte rettlinjede bevegelsen

Hastigheten avhengig av tiden V (t) til en mobil som beveger seg langs en linje med konstant akselerasjon ved og innledende hastighet V_enten  forskjellig fra 0. Denne bevegelsen er kjent som jevnt variert rettlinjet bevegelse Og hastighetsligningen er:

Kan tjene deg: tetthet

v (t) = v_enten + PÅ

Termisk ekspansjon

Et annet naturfenomen hvis variasjon er lineær er økningen i lengden som opplever en stang eller en ledning når den blir oppvarmet.

Når temperaturen på et hvilket som helst objekt øker, er dimensjonene også, og denne økningen avhenger av temperaturendringen ΔT og en mengde som kalles Lineær utvidelseskoeffisient betegnet med den greske bokstaven α:

L = l_enten + α Δt

I dette uttrykket er L den endelige lengden på objektet og l_enten er dens første lengde.

Plassering av en mobil med konstant hastighet

En mobil med hastighet Konstant beveger seg alltid i en rett linje. Hvis den rette linjen er den horisontale aksen X, er posisjonen x (t) når som helst gitt av:

x (t) = x_enten + Vt

Hvor x_enten Det er startposisjonen, v er hastigheten og t er tiden. På denne måten sies det at X -posisjonen varierer lineært med tiden t.

En person status

Leger og antropologer kan estimere statens status ved å måle lengden på lårbenet.

Jo høyere en person, jo lengre har bena, så det er lineære modeller for å forutsi høyden til en voksen person h (i tommer) hvis lengden L (også i tommer) av dens lårben er kjent, i henhold til ligningen:

H = 1.880⋅L + 32.010

Temperaturskala

Celsius og Fahrenheit skalaer brukes daglig for å måle temperaturer. Denne siste skalaen brukes ofte i engelsktalende land. Det er en ekvivalens å flytte fra hverandre:

F = (9/5) C + 32

Hvor F er temperaturen i grader Fahrenheit og C er temperaturen i grader Celsius.

Trykk og dybde

Det absolutte trykket P i en inkomprimerbar væske som vann, hvis konstante tetthet er ρ, varierer avhengig av dybden H som:

Det kan tjene deg: Horisontal skyting: Kjennetegn, formler og ligninger, øvelser

P = p_enten + ρgh

Hvor p_enten Det er trykket på væskens frie overflate. Hvis væsken er i en beholder som er åpen for atmosfæren, er dette trykket ganske enkelt atmosfæretrykket P_ATM, Å kunne skrive da:

P = p_ATM + ρgh

Atmosfærisk trykk ved havnivået er omtrent 101 kPa. Dette forholdet mellom P og H betyr at trykket øker lineært med dybden.

Trykket som dykkeren opplever varierer lineært med dybde. Kilde: Ahmed Samy/Pexels.

Trening løst

Kjørekostnad

Den månedlige kostnaden for å håndtere en bil inkluderer en månedlig fast kostnad C_enten Pluss kostnadene for kjørelengde eller kjørelengden reiste hver måned. En sjåfør observerer at ledelseskostnaden i løpet av en måned var $ 380 for $ 480, og den påfølgende måneden var det $ 460 per 800 miles.

La mengden miles bli reist per måned av sjåføren, med dataene som er gitt, finn:

a) Den lineære variasjonen mellom C og D.

b) Hvor mye vil bilen koste per måned på en tur på 1500 kilometer?

c) Grafen til C versus D.

Løsning på

Anta at variablene har et forhold gitt av:

C = c_enten + TIL.d

Hvor a og c_enten De er konstante for å bestemme. A er skråningen på linjen som grafisk representerer forholdet mellom C og D. CO er kuttet med den vertikale aksen, den månedlige faste kostnaden som sjåføren må betale for bare faktum å ha bilen tilgjengelig. Her kan for eksempel vedlikeholds- og skattekostnader inkluderes.

Å utvetydig bestemme en linje er det nødvendig å kjenne skråningen. For dette har vi poengene:

P₁: 480 miles, $ 380

P₂: 800 miles, $ 460

Disse punktene, av koordinater (d, c) eller (avstand, kostnad) er analoge med koordinatpunktene (x, y) til det kartesiske planet, hvilke endringer er navnene. Hellingen til linjen blir deretter gitt av:

Kan tjene deg: skrå fly

A = (c₂ - C₁)/(D₂ - d₁)

A = [(460 - 380) $ / (800 - 480) miles] = (1/4) $ / mil

Linjens helning representerer kostnaden per kilometer, på denne måten:

C = c_enten + TIL.D = CO + (1/4).d

For å bestemme den grunnleggende kostnaden C_enten Denne ligningen er tatt og et av punktene vi vet tilhører den, for eksempel P₁:

380 $ = C_enten + [(1/4) $ / mil] . 480 mil → 380 $ = C_enten + 120 dollar

C_enten = $ 260

Nå kan vi formulere den lineære variasjonsmodellen som:

C = 260 + (1/4) D

Løsning b

Den månedlige kostnaden for å reise 1500 miles er:

C = 260 + (1/4) x 1500 $ = $ 635

Løsning c

Grafen til C som en funksjon av D er:

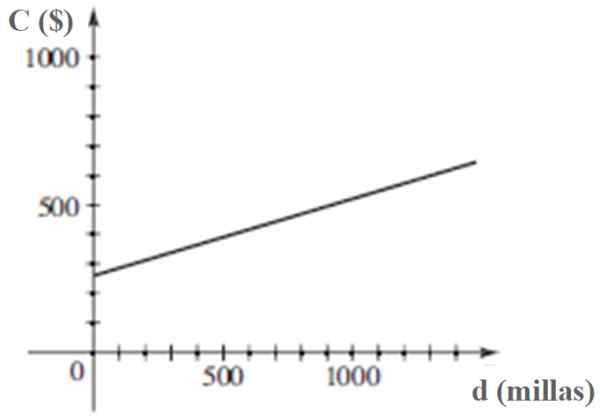Kostnaden C for å håndtere et kjøretøy er en lineær funksjon av avstanden som er tilbakelagt D. Kilde: Stewart, J. Forkalkning.

Referanser

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
2. Hoekenga, ca. Lineære ligninger i vitenskap. Gjenopprettet fra: Visionlearning.com.
3. Hoffman, J. Valg av matematikkproblemer. Volum 2.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
6. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.