Balancervektorberegning, eksempler, øvelser

Han Balanserende vektor Det er den som kontrasterer den resulterende vektoren, og derfor er den i stand til å balansere et system, siden det har samme størrelse og samme retning, men i motsetning til dette.

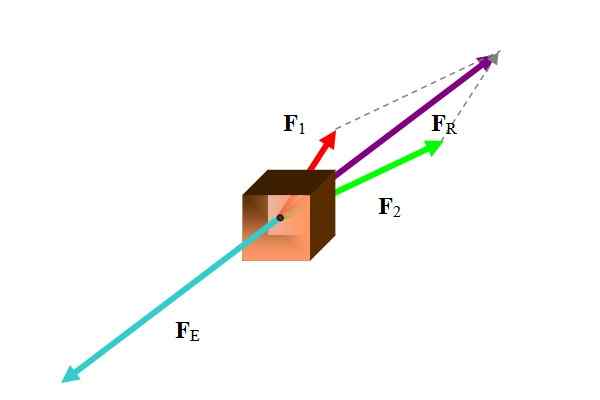
Ved flere anledninger refererer balanseringsvektoren til en kraftvektor. For å beregne balanseringskraften er den resulterende kraften først, som vist i følgende figur:

Figur 1. På et organ Two Forces Act hvis resulterende er balansert med makt i turkis farge. Kilde: Selvlaget.

Det er forskjellige metoder for å utføre denne oppgaven, i henhold til dataene som er aktuelle. Ettersom kreftene er vektorer, er resultatet vektorsummen til de deltagende kreftene:

F_R = F₁ + F₂ + F₃ +  .. .

Blant metodene som skal brukes er grafiske metoder som polygonalt, parallellogram og analysemetoder som nedbrytning av krefter i deres kartesiske komponenter. I eksemplet ble figuren brukt parallellogrammetoden.

Når den resulterende kraften er funnet, er balanseringskraften nettopp den motsatte vektoren.

Ja F_OG Det er balanseringsstyrken, så blir det oppfylt det F_OG Anvendt på et bestemt tidspunkt, garanterer det balansen i systemoversettelsen. Hvis det er en enkelt partikkel, vil den ikke bevege seg (eller kanskje den gjør det med konstant hastighet), men hvis det er et utvidet objekt, vil det fortsatt ha muligheten til å snu:

F_R + F_OG = 0

[TOC]

Eksempler

Balanseringskreftene er til stede på alle sider. Vi er selv balansert av styrken som stolen utøver for å kompensere for vekten. Gjenstandene som finnes i ro: bøker, møbler, taklamper og et stort antall mekanismer, blir kontinuerlig balansert av krefter.

Kan tjene deg: Inelastiske sjokk: I en dimensjon og eksempler

For eksempel er en hvilebok på et bord balansert av normalen som den utøver på boka, og forhindrer at den faller. Det samme gjelder kjeden eller kabelen som holder lampen som henger fra taket i et rom. Kablene som holder en belastning distribueres vekten gjennom spenningen i dem.

I en væske er noen gjenstander i stand til å flyte og forbli i ro, siden vekten er balansert av en stigende kraft som utøves av væsken, kalt trykk.

Ulike mekanismer må være balansert og kjenne balanseringskraftvektoren som stenger, bjelker og søyler.

Når du bruker en balanse, er det nødvendig å på en eller annen måte balansere vekten til objektet med en kraft som er likeverdige, enten legge til vekter eller med kilder.

Forces Table

Forces -tabellen brukes i laboratoriet for å bestemme den balanserte styrken. Den består av en sirkulær plattform, hvor du har den øvre visningen i figuren, og som har en transportør for å måle vinkler.

Ved kantene av bordet er det remskiver som strenger som holder vekter og som konvergerer i en bøyle som er i sentrum.

For eksempel er to vekter hengt. Spenningene som genereres på strengene av disse vektene er tegnet i rødt og blått i figur 2. En tredje veier grønn, kan balansere den resulterende kraften til de to andre og holde systemet i balanse.

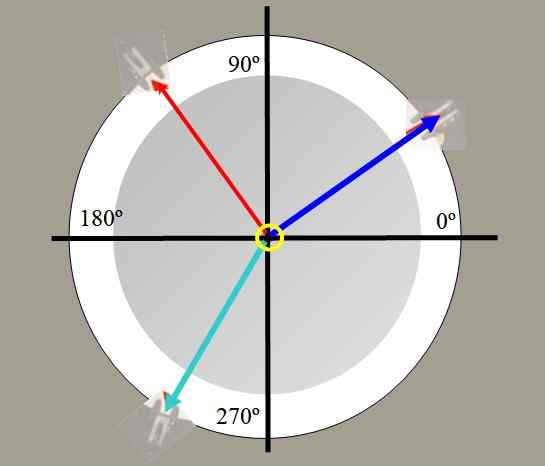Figur 2. Vis fra toppen av styrkenes bord. Kilde: Selvlaget.

Med tabellen over krefter kan du verifisere kreftens vektorkarakter, dekomponere krefter, finne balanseringskraften og bekrefte Lamys teorem:

Kan tjene deg: sol

Hvis en Kroppen er i likevekt takket være tre koplanære, samtidige og ikke -kolineale (ikke -parallelle) styrker, kalt TIL, B og C, Forholdet mellom disse kreftene er som følger:

A/ sin α = b/ sen β = c/ sen γ

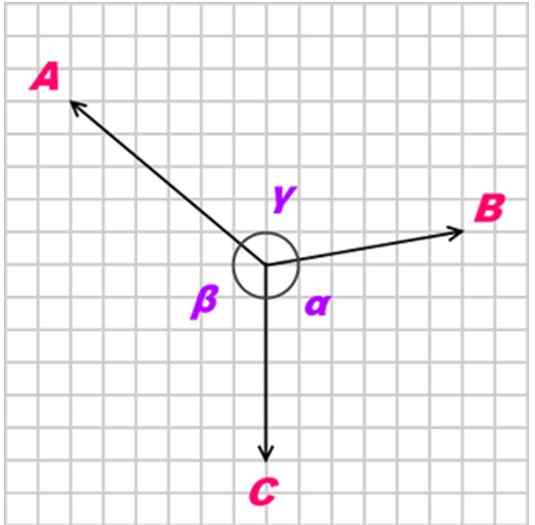Figur 3. Lamys teorem gjelder samtidig og koplanære styrker. Kilde: Wikimedia Commons.

Løste øvelser

-Oppgave 1

I kreftene tabell i figur 2 veier 225 g (blå spenning) og 150 g (rød spenning) henges, med vinklene vist. Finn verdien av balanseringskraften og vinkelen som denne formen med den vertikale aksen.

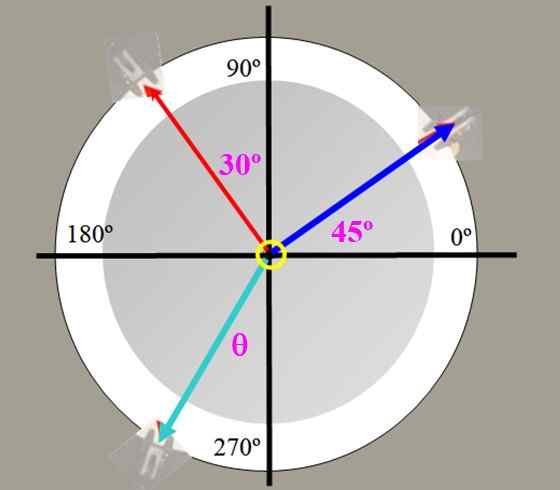Figur 4. Krefter bord for trening 1.

Løsning

Problemet kan arbeides med vektene uttrykt i gram (krefter). La s₁ = 150 gram og P₂ = 225 gram, de respektive komponentene i hver er:

P_1x = 225 . cos 45º g = 159.10 g; P_1y = 225 . cos 45º g = 159.10 g

P_2x = -150 . Sen 30º G = -75.00 g; P_{2 og} = 150 . Cos 30º g = 129.90 g

Den resulterende vekten P_R Komponentene legger algebraisk til:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Balansegangen P_OG er den motsatte vektoren P_R:

P_Eks = -84.10 g

P_Hei = -289.00 g

Størrelsen på balansegangen beregnes med:

P_OG = (S_Eks² + P_Hei²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

Vinkelen θ på figuren er:

θ = arctg (-84.10 / -289.00) = 16.2. med hensyn til aksen og negativ.

-Oppgave 2

Finn balanseringsvektoren til systemet vist på figuren, vel vitende om at hver kvadrat måler 10 m side.

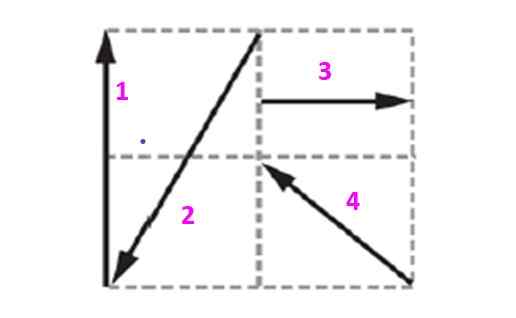Figur 5. Diagram for eksemplet løst 2.

Løsning

Vektorene i dette rutenettet vil bli uttrykt i form av enheten og ortogonale vektorer Yo og J som bestemmer flyet. Vektor 1, som vil bli betegnet som v₁ Den har 20 m størrelse og er rettet vertikalt oppover. Det kan uttrykkes som:

Det kan tjene deg: Strålingsvarmeoverføring (med eksempler)

v₁ = 0 Yo +tjue J m

Fra tegningen observeres det at vektor 2 er:

v₂ = -10 Yo - tjue J m

Vektor 3 er horisontal og peker i den positive adressen:

v₃ = 10 Yo + 0 J  m

Endelig er vektor 4 skrå 45 º, siden det er diagonalen til torget, og derfor måler komponentene det samme:

v₄ = -10 Yo + 10 J m

Merk at tegnet -.

Den resulterende vektoren oppnås ved å legge til komponentkomponent:

v_R = -10 Yo + 10 J m

Da er balanseringsvektoren til systemet:

v_OG = 10 Yo - 10 J m

Referanser

1. Beardon, t. 2011. En introduksjon til vektorer. Gjenopprettet fra: Nrich.Matte.org.
2. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley. 38-52.
3. Figueroa, d. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk.31-68.
4. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Editorial Company. 15-53.
6. Tilleggskalkulatorvektor. Gjenopprettet fra: 1728.org
7. Vektorer. Gjenopprettet fra: Wikibooks.org