Gratis vektorer egenskaper, eksempler, øvelser

De gratis vektorer De er de som er fullt spesifisert etter størrelsesorden, deres retning og deres betydning, uten at det er nødvendig å indikere et søknadspunkt eller et bestemt opprinnelse.

Siden uendelige vektorer kan trekkes på denne måten, er en fri vektor ikke en unik enhet, men et sett med parallelle og identiske vektorer som er uavhengige av stedet der de ligger.

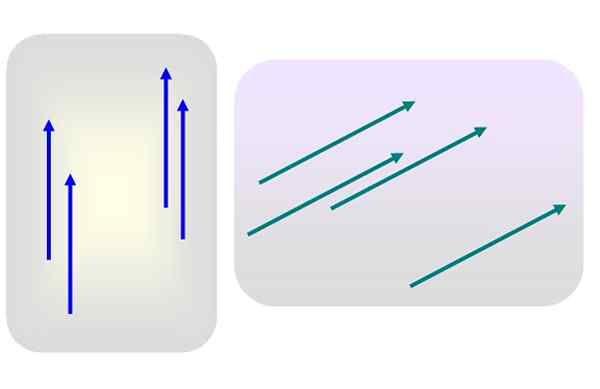
Figur 1. Forskjellige gratis vektorer. Kilde: Selvlaget.

La oss si at det er flere vektorer av størrelses- 3 rettet vertikalt opp, eller størrelsesorden 5 og skrå til høyre, som i figur 1.

Ingen av disse vektorene blir spesielt brukt på et eller annet punkt. Da er noen av de blå eller grønne vektorene representative for deres respektive gruppe, siden dens egenskaper - modul, retning og sans - ikke blir endret i det hele tatt når de blir overført til et annet sted i flyet.

En gratis vektor er vanligvis betegnet i trykt tekst med en liten og dristig bokstav, for eksempel v. Eller med små bokstaver og en pil på toppen hvis det er en manuskripttekst.

[TOC]

 Eksempler

Fordelen som gratis vektorer har er at de kan flyttes etter plan eller rom og opprettholde egenskapene sine, siden enhver representant for settet er like gyldig.

Det er grunnen til at i fysikk og mekanikk ofte brukes. For eksempel for å indikere den lineære hastigheten til et fast stoff som beveger seg, er det ikke nødvendig å velge et bestemt punkt i objektet. Da oppfører hastighetsvektoren seg som en fri vektor.

Et annet eksempel på fri vektor er styrets par. EN par Den består av to krefter med like stor størrelse og retning, men av motsatte sanser, påført i forskjellige punkter med et faststoff. Effekten av et par er ikke å overføre objektet, men å forårsake en rotasjon takket være øyeblikk produsert.

Figur 2 viser et par krefter påført ratt. Gjennom krefter F₁ og F₂, Dreiemomentet som snur rattet rundt midten er opprettet og i en timeplan.

Det kan tjene deg: Bornitrid (BN): Struktur, egenskaper, innhenting, bruk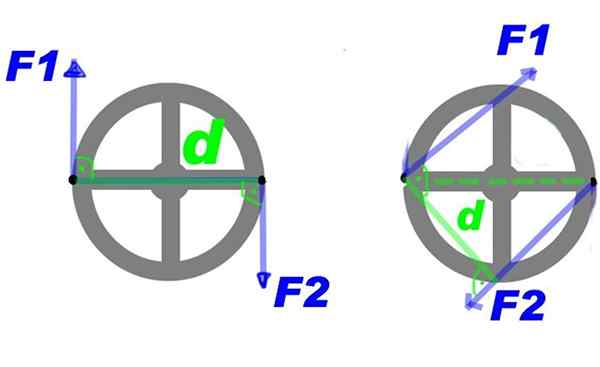 Figur 2. Et par krefter påført et ratt gir en scoringssving. Kilde: Bensko [Public Domain].

Du kan gjøre noen endringer på paret og fortsette å oppnå den samme roterende effekten, for eksempel øke kraften, men redusere avstanden mellom dem. Eller opprettholde styrke og avstand, men bruk paret på et annet par punkter på rattet, det vil si snu dreiemomentet rundt midten.

Tid for styrets par eller ganske enkelt par, Det er en vektor hvis modul er Fd og er vinkelrett på hjulplanet vinkelrett. I eksemplet som vises av stevne, gir tidsving negativ fornuft.

Egenskaper og egenskaper

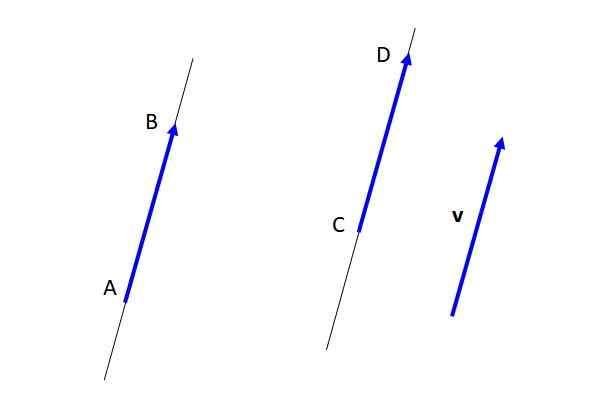
I motsetning til den frie vektoren V, vektorene AB og CD De er faste (se figur 3), siden de har spesifisert utgangspunkt og ankomstpunkt. Men å være utstyr med hverandre, og på sin side med vektoren v, De er representative for den frie vektoren v.

Figur 3. Gratis vektorer, utstyr og faste vektorer. Kilde: Selvlaget.

De viktigste egenskapene til frie vektorer er følgende:

-Hvilken som helst vektor AB (Se figur 2) Det er som sagt representativt for den frie vektoren v.

-Modulen, retningen og betydningen er den samme i enhver gratis vektorrepresentant. I figur 2, vektorene AB og CD De representerer den frie vektoren v Og de er utstyr.

-Gitt et punkt P med rom, er det alltid mulig å finne en gratis vektorrepresentant v hvis opprinnelse er i P og sa at representant er unik. Dette er den viktigste egenskapen til gratis vektorer og den som gjør dem så allsidige.

Kan tjene deg: Europa (satellitt): Kjennetegn, komposisjon, bane, bevegelse

-En seilet fri vektor er betegnet som 0 Og det er settet med alle vektorer som mangler størrelse, retning og mening.

-Hvis vektoren AB representerer den frie vektoren v, Deretter vektoren Ba representerer den frie vektoren -v.

-Notasjon vil bli brukt V³ å utpeke settet med alle romfrie vektorer og V² Å utpeke alle frie vektorer av flyet.

Løste øvelser

Med gratis vektorer kan du utføre følgende operasjoner:

-Addisjon

-Subtraksjon

-Multiplikasjon av klatring med en vektor

-Skalarprodukt mellom to vektorer.

-Kryss produkt mellom to vektorer

-Lineær kombinasjon av vektorer

Og mer.

-Oppgave 1

En student har til hensikt å svømme fra et punkt på bredden fra den ene elven til en annen som er nettopp foran. For å ikke oppnå noe direkte med en hastighet på 6 km / t, i vinkelrett retning, har strømmen en hastighet på 4 km / t som avleder den.

Beregn hastigheten som følge av svømmeren og hvor mye som blir avledet av strømmen.

Løsning

Svømmerens utvidede hastighet er vektorsummen av hastigheten (med hensyn til elven, tegnet vertikalt opp) og hastigheten på elven (trukket fra venstre til høyre), som utføres som indikert i figuren nedenfor:

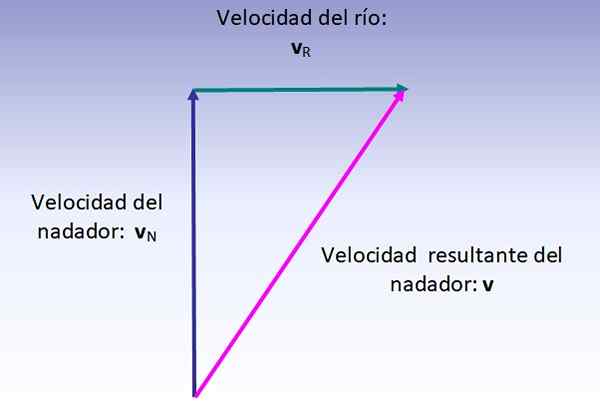
Størrelsen på den resulterende hastigheten tilsvarer hypotenusen til høyre trekant vist, derfor:

V = (6² + 4²) ^½ km/h = 7.2 km/t

Adressen kan beregnes med vinkel med hensyn til vinkelrett på kysten:

α = ARCTG (4/6) = 33.7. eller 56.3. angående kysten.

Oppgave 2

Finn tidspunktet for styrets par vist på figuren:

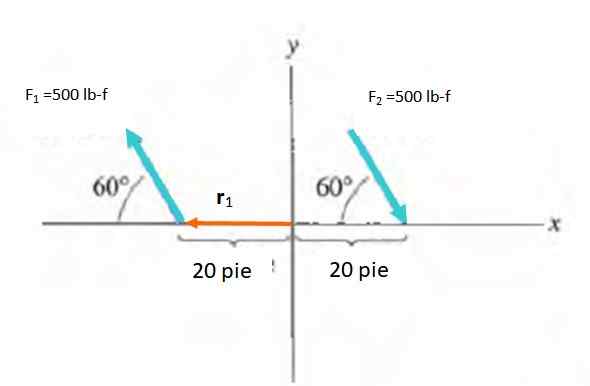
Løsning

Øyeblikket beregnes av:

Kan tjene deg: Inelastiske sjokk: I en dimensjon og eksempler

M = r x F

Øyeblikkets enheter er LB-F.fot. Siden dreiemomentet er i planet på skjermen, er øyeblikket rettet vinkelrett på det, enten utover eller innover.

Ettersom eksemplets dreiemoment har en tendens til å vri objektet som det brukes på (som ikke er vist på figuren) i en plan, blir dette øyeblikket vurdert ved å peke på skjermen og med et negativt tegn.

Øyeblikkets størrelse er m = f.d.sin a, å være i vinkelen mellom kraften og vektoren r. Du må velge et punkt for å beregne øyeblikket, som er en gratis vektor. Opprinnelsen til referansesystemet er valgt, derfor r Går fra O til anvendelsespunktet for hver styrke.

M₁ = M₂ = -Fdsen60º = -500 . tjue .Sen 60º LB-F . Fot = -8660.3 lb-f . fot

Netto øyeblikk er summen av m₁ og M₂: -17329.5 lb-f . fot.

Referanser

1. Beardon, t. 2011. En introduksjon til vektorer. Gjenopprettet fra: Nrich.Matte.org.
2. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley. 38-52.
3. Figueroa, d. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk.31-68.
4. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Editorial Company. 15-53.
6. Tilleggskalkulatorvektor. Gjenopprettet fra: 1728.org
7. Vektorer. Gjenopprettet fra: det er.Wikibooks.org