Vektorer i verdensrommet hvordan du kan graf, applikasjoner, øvelser

EN vektor i rommet Det hele er representert av et koordinatsystem gitt av x, og og z. Nesten alltid flyet Xy Det er planet for den horisontale overflaten og aksen z representerer høyden (eller dybden).

De kartesiske koordinataksene vist i figur 1, del rommet i 8 regioner som kalles Octavers, analog med hvordan aksene x - og Del flyet i 4 kvadranter. Vi vil da ha 1 oktant, 2. ocanto og så videre.

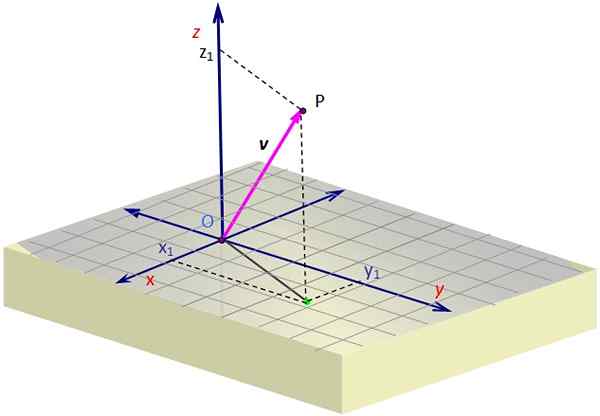
Figur 1. En vektor i rommet. Kilde: Selvlaget.

Figur 1 inneholder en representasjon av en vektor v i rommet. Noe perspektiv er nødvendig for å skape illusjonen av tre dimensjoner på skjermen på skjermen, som oppnås ved å trekke en skrå visning.

For å tegne en 3D -vektor, må du hjelpe de stiplede linjene som bestemmer koordinatene til projeksjonen eller "skyggen" av nettet v Over overflaten x-og. Denne projeksjonen begynner i O og slutter på det grønne punktet.

Når du er der, må du fortsette med vertikalen til høyden (eller dybden) som er nødvendig i henhold til verdien av z, til du kommer til P. Vektoren er hentet fra O og slutter i P, som i eksemplet er i 1. OCant.

[TOC]

applikasjoner

Vektorer i verdensrommet er mye brukt i mekanikk og andre grener av fysikk og ingeniørfag, siden strukturene som omgir oss krever geometri i de tre dimensjonene.

Posisjonsvektorer i rommet brukes til å plassere objekter med hensyn til et referansepunkt kalt opprinnelse ENTEN. Derfor er de også nødvendige verktøy i navigasjonen, men det er ikke alt.

Kan tjene deg: Elektromagnetiske bølger: Maxwell -teori, typer, egenskaper

Kreftene som virker på strukturer som bolter, støtter, kabler, stag og mer er vektor natur og er orientert i rommet. For å vite virkningen av den, er det nødvendig å kjenne adressen din (og også søknadspunktet ditt).

Og ofte er retningen til en styrke kjent med to punkter i verdensrommet som tilhører dens handlingslinje. På denne måten er styrken:

F = F eller

Hvor f er størrelsen eller modulen for kraft og eller Det er enhetsvektoren (modul 1) rettet langs handlingslinjen til F. 

3D -vektornotasjon og representasjoner

Før du løser noen eksempler, vil notasjonen av 3D -vektorer bli gjennomgått kort.

I eksemplet på figur 1 har vektor V, hvis opprinnelsessted sammenfaller med opprinnelsen eller og hvis avslutning er punkt P, koordinater x og z positivt, mens koordinat og Det er negativt. Disse koordinatene er: x₁, og₁, z₁, som nettopp er koordinatene til P.

Så hvis vi har en vektor knyttet til opprinnelsen, det vil si, hvis utgangspunkt sammenfaller med O, er det veldig enkelt å indikere koordinatene, som vil være de av det ekstreme punktet eller P. For å skille mellom et punkt og en vektor, vil vi bruke for de nyeste fetme bokstavene og parentesene, som dette:

v = < x₁, og₁, z₁ >

Mens punkt P er betegnet med parenteser:

P = (x₁, og₁, z₁)

En annen representasjon benytter seg av enhetsvektorer Yo, J og k som definerer de tre plassbeskrivelsene i aksene x, og og z henholdsvis.

Disse vektorene er vinkelrett på hverandre og utgjør en Ortonormal base (Se figur 2). Dette betyr at en 3D -vektor kan skrives i form av dem som:

Kan tjene deg: bølgende bevegelse: egenskaper, bølger typer, eksempler

v = v_x Yo + v_og J + v_z k

Vinkler og cosenos direktører av en vektor

Figur 2 viser også regissørene γ -vinkler₁, γ₂ og γ₃ enn vektoren v henholdsvis med aksene x, og og z. Når du kjenner disse vinklene og vektorenes størrelse, er dette fullstendig bestemt. I tillegg oppfyller styremedlemmers kosiner følgende forhold:

(Cos γ₁)² + (Cos γ₂)² + (Cos γ₃)² = 1

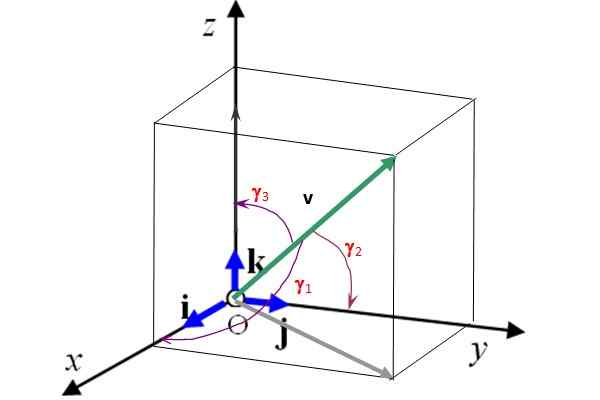Figur 2. Enhetsvektorer I, J og K bestemmer de 3 foretrukne romets retninger. Kilde: Selvlaget.

Løste øvelser

-Oppgave 1

I figur 2 er y -vinklene₁, γ₂ og γ₃ enn vektoren v av modul 50 form med koordinataksene er henholdsvis: 75.0º, 60.0º og 34.3. Finn de kartesiske komponentene i denne vektoren og representer den med tanke på enhetsvektorene Yo, J og k.

Løsning

Projeksjonen av vektoren v på aksen x er v_x = 50 . Cos 75º = 12.941. Tilsvarende projeksjonen av v på aksen og er v_og = 50 cos 60 º = 25 og til slutt på aksen z er v_z = 50. cos 34.3. = 41.3. Nå v kan uttrykkes som:

v = 12.9 Yo + 25.0 J + 41.3 k

-Oppgave 2 

Finn spenninger i hver av kablene som holder bøtta på figuren som er i likevekt, hvis vekten av dette er 30 n.

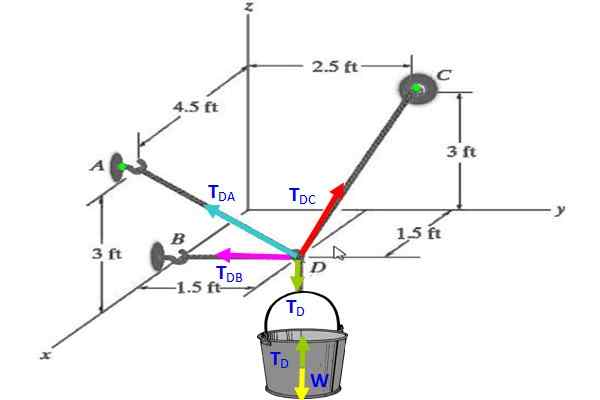Figur 3. Spenningsdiagram for oppgave 2.

Løsning

På bøtta indikerer det frie kroppsdiagrammet det T_D (grønn) kompenserer for vekt W (gul), derfor t_D = W = 30 n.

I knuten, vektoren T_D  Det er rettet vertikalt ned, da:

T_D = 30 (-k) N.

For å etablere de gjenværende spenningene må du følge følgende trinn:

Trinn 1: Finn koordinatene til alle punkter

A = (4.5; 0; 3) (A er på veggplanet X-Z)

B = (1.5; 0; 0) (B er på x -aksen)

Kan tjene deg: adresse (fysisk)

C = (0, 2.5, 3) (C er på veggplanet og z)

D = (1.5; 1.5; 0) (D er på det horisontale planet  x-og)

Trinn 2: Finn vektorene i hver retning ved å trekke fra koordinatene til slutten og begynnelsen

Gir =

DC =

Db =

Trinn 3: Beregn moduler og enhetsvektorer

En enhetsvektor oppnås ved uttrykk: eller = r / r, med r (ved fet skrift) å være vektoren og r (uten fet) modulen til nevnte vektor.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; DC = ((-1.5) ² + 1² + 3²)^½ = 3.5

eller_Gir = 4.5 =

eller_DC = 3.5 =

eller_Db =

eller_D =

Trinn 4: Uttrykk alle spenninger som vektorer

T_Gir = T_Gir eller_Gir = T_Gir

T_DC = T_DC eller_{DC =}  T_DC

T_Db = T_Db eller_Db = T_Db

 T_D = 30

Trinn 5: Bruk den statiske likevektstilstanden og løse ligningssystemet

Til slutt blir den statiske balansetilstanden brukt på bøtta, slik at vektorsummen til alle krefter på knuten er ugyldig:

T_Gir + T_DC + T_Db + T_D = 0

Ettersom spenningene er i verdensrommet, vil det føre til et tre ligningssystem for hver komponent (x, og og z) av spenninger.

0.67 t_Gir -0.43 t_DC + 0 t_Db = 0

-0.33 t_Gir + 0.29 t_DC - T_Db = 0

0.67 t_Gir + 0.86 t_DC +0 t_Db - 30 = 0

Løsningen er: t_Gir = 14.9 n; T_Gir = 23.3 n; T_Db = 1.82 n

Referanser

1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley. 38-52.
2. Figueroa, d. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk.31-68.
3. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Editorial Company. 15-53.
5. Tilleggskalkulatorvektor. Gjenopprettet fra: 1728.org