Colineale vektorer

Vi forklarer hva colineale vektorer er, Colineal -vektorsystemet, og vi legger flere eksempler

Hva er de kollineale vektorene?

De Colineale vektorer De er en av de tre typene eksisterende vektorer. Dette er de vektorene som er i samme retning eller handlingslinje. Dette betyr følgende: To eller flere vektorer vil være colineal hvis det er tilfelle at de er ordnet i linjer som er parallelle med hverandre.

En vektor er definert som en styrke påført en kropp og er preget av å ha en retning, en sans og en skala. Vektorer kan finnes i planet eller i rommet og kan være av forskjellige typer: colineale vektorer, samtidige vektorer og parallelle vektorer.

Når er det kollineale vektorer?

Vektorene er colineal hvis virkningen av en er nøyaktig den samme virkningen av alle andre vektorer, uavhengig av størrelse og retning på hver av vektorene.

Vektorer brukes som representasjoner på forskjellige områder som matematikk, fysikk, algebra og også i geometri, der vektorer bare er colineal når retningen deres er den samme, uavhengig av at deres betydning ikke er.

Eksempler på colineale vektorer

• To eller flere vektorer er colineal hvis forholdet mellom koordinater er det samme.

Eksempel 1

Du har vektorer m = m_x; m_y og n = n_x; N_. Disse er kollinære hvis:

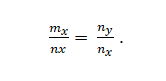
Eksempel 2

Det kan bestemmes om vektorene j = 3,6,15 og p = 1,2,5 er kollinære gjennom forholdet til deres koordinater, som du må være proporsjonal med hverandre; det er å si: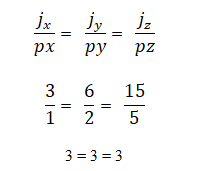

• To eller flere vektorer er colineal hvis produktet eller vektormultiplikasjonen er lik null (0). Dette er fordi, i koordinatsystemet, er hver vektor preget av sine respektive koordinater, og hvis disse er proporsjonale med hverandre, vil vektorene være kollinære. Dette uttrykkes som følger:

Kan tjene deg: tilsvarende sett: Hva er, forklaring, eksempler

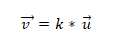
Eksempel 1

Du har vektorer a = (10, 5) og b = (6, 3). For å avgjøre om de er colineal, blir den avgjørende teorien brukt, som etablerer likheten mellom kryssprodukter. På denne måten må du:

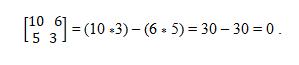
Colineal vektorsystem

Colineale vektorer er representert grafisk ved å bruke retningen og retningen til disse - med tanke på at disse må gå gjennom applikasjonspunktet - og modulen, som er en spesifikk skala eller lengde.

Det colineale vektorsystemet dannes når to eller flere vektorer virker på et objekt eller et legeme, som representerer en kraft og virker i samme retning.

For eksempel, hvis to colineale krefter blir brukt på et organ, vil den resulterende av disse bare avhenge av den forstand de handler. Det er tre tilfeller, som er:

Colineale vektorer med motsatte sanser

Det resulterende av to colineale vektorer er lik summen av disse:

R = ∑ f = f₁ + F_2.

Eksempel

Hvis to F -styrker virker på en vogn₁ = 40 n og f₂ = 20 n i motsatt retning (som vist på bildet), er resultatet:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

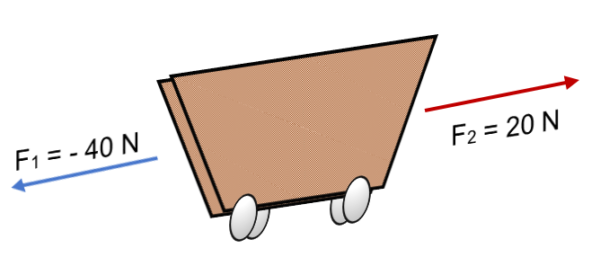Det negative tegnet uttrykker at kroppen vil bevege seg til venstre, med en styrke som tilsvarer 20 n.

Colineale vektorer i samme forstand

Størrelsen på den resulterende kraften vil være lik summen av colineale vektorer:

R = ∑ f = f₁ + F_2.

Eksempel

Hvis to F -styrker virker på en vogn₁ = 35 n og f₂ = 55 N i samme retning (som vist på bildet), er resultatet:

R = ∑ f = 35 n + 55n.

R = 90 n.

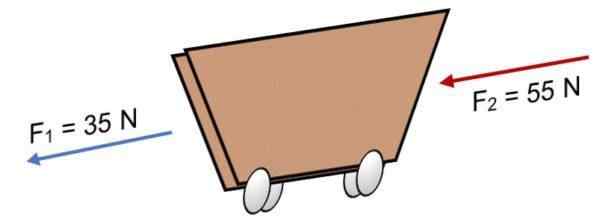
Det positive resultatet indikerer at kollineale vektorene virker til venstre.

Det kan tjene deg: Regel T: Karakteristikker, slik at det er eksempler

Colineale vektorer med like størrelser og motsatte sanser

Resultatet av de to kollineale vektorene vil være lik summen av de kollineære vektorene:

R = ∑ f = f₁ + F_2.

Ettersom kreftene har samme størrelse, men i motsatt retning -det vil si at en vil være positiv og en annen negativ -ved å legge til de to kreftene vil resultatet være lik null.

Eksempel

Hvis to F -styrker virker på en vogn₁ = -7 n og f₂ = 7 n, som har samme størrelse, men i motsatt retning (som vist på bildet) er resultatet:

R = ∑ f = (-7 n) + 7n.

R = 0.

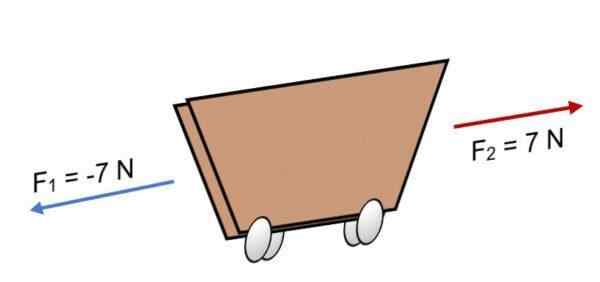
Ettersom resultatet er lik 0, betyr det at vektorer balanserer med hverandre og derfor er kroppen i balanse eller hvile (den vil ikke bevege seg).

Forskjell mellom colineal og samtidig vektorer

Colineale vektorer er preget av å ha samme retning på samme linje, eller fordi de er parallelle med en linje; Det vil si at de er parallelle linjedirektorer vektorer.

For deres del er samtidig vektorer definert fordi de er i forskjellige handlingslinjer som blir oppfanget på et enkelt punkt.

Med andre ord, de har samme opprinnelsespunkt eller ankomst -Regardless av modulen deres, mening eller retning -former en vinkel mellom dem.

Samtidig vektorsystemer løses ved matematiske eller grafiske metoder, som er parallellogrammetoden for krefter og metode for kreftene polygon. Gjennom disse vil verdien av en resulterende vektor bli bestemt, noe som indikerer retningen en kropp vil bevege seg.

I utgangspunktet er hovedforskjellen mellom de kollinære og samtidige vektorene handlingen de handler: Collineals opptrer i samme linje, mens de samtidige i forskjellige.

Kan tjene deg: System of Equations: Solution Methods, Eksempler, øvelser

Det vil si at de kollinære vektorene virker i et enkelt plan, "x" eller "y"; Og den samtidige handlingen i begge flyene, fra samme punkt.

Colineale vektorer er ikke på et tidspunkt, som de samtidige gjør det, fordi de er parallelle med hverandre.

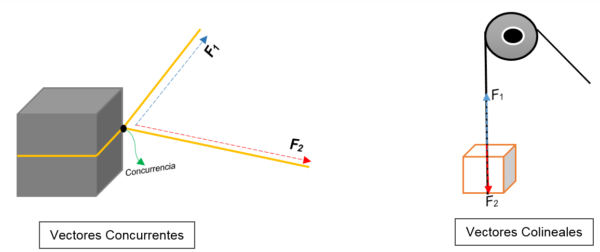
I venstre bilde kan du se en blokk. Den er bundet med et tau og knuten deler det inn i to; Når du blir funnet mot forskjellige orienteringer og med forskjellige krefter, vil blokken bevege seg mot samme retning.

To vektorer blir representert på et tidspunkt (blokken), uavhengig av modul, retning eller retning.

På den annen side vises på riktig bilde en remskive som løfter en boks. Tauet representerer handlingslinjen; Når det blir stoppet, virker to krefter (vektorer) på den: en spenningsstyrke (når du klatrer opp blokken) og en annen kraft, som utøver vekten på blokken. Begge har samme retning, men i motsatte sanser; De er ikke enig på et tidspunkt.