Equipocent Vectors Definisjon, notasjon, øvelser

To eller flere Vektorer er utstyr Hvis de har samme modul, er den samme retningen og like sansen, selv når opprinnelsesstedet er annerledes. Husk at egenskapene til en vektor er nettopp: opprinnelse, modul, retning og sans. 

Vektorer er representert med et orientert eller pilsegment. Figur 1 viser representasjon av flere vektorer i planet, hvorav noen er utstyr i henhold til definisjonen opprinnelig gitt.

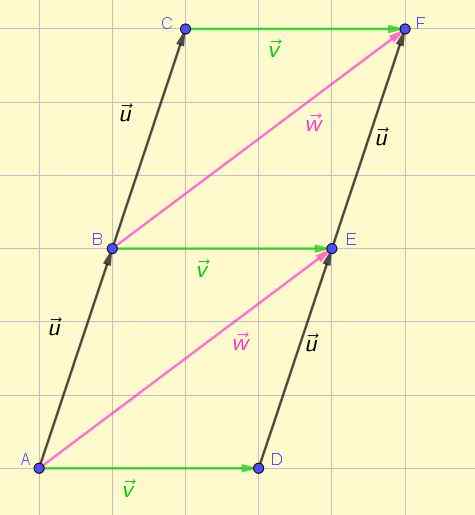Figur 1. Utstyr og ikke -utstyrsvektorer. Kilde: Selvlaget.

Fra første øyekast er det mulig å sette pris på at de tre grønne vektorene har samme størrelse, samme retning og samme sans. Det samme kan bekreftes om de to rosa vektorene og de fire svarte vektorene.

Tallrike naturstørrelser har en vektoratferd, slik er tilfellet med hastighet, akselerasjon og styrke, for bare å nevne noen. Derav viktigheten av å karakterisere dem på riktig måte.

[TOC]

Notasjon for vektorer og utstyr

For å skille vektorbeløpene for skalarmengdene, brukes ofte svart -type bokstav eller en pil på bokstaven. Når du jobber med håndvektorer, er det nødvendig å skille dem med pilen, og når et trykt medium brukes, brukes dristige.

Vektorer kan nektes å indikere utgangspunkt eller opprinnelse og deres ankomstpunkt. For eksempel AB, BC, AV og Ef av figur 1 er imidlertid vektorer AB, BC, AV og Ef De er skalare mengder eller tall som indikerer størrelsen, modulen eller størrelsen på deres respektive vektorer.

For å indikere at to vektorer er utstyr, brukes symbolet "∼ ". Med denne notasjonen kan vi i figuren påpeke følgende vektorer som er utstyr med hverandre:

Kan tjene deg: Kinetisk energi: Kjennetegn, typer, eksempler, øvelser

ABOBC∼DE∼EF 

De har alle samme størrelse, retning og mening. Oppfyller derfor regelverket som er angitt ovenfor.

Gratis, glidende og motsatte vektorer

Noen av vektorene i figuren (for eksempel AB) er en representant for settet med alle faste faste vektorer. Dette uendelige settet definerer klassen av gratis vektorer eller.

eller = AB, BC, fra, EF, ..

En alternativ notasjon er som følger:

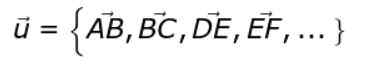
Hvis fet skrift eller pil ikke er plassert på toppen eller, Vi vil referere til vektorkodulen eller.

Gratis vektorer brukes ikke på et bestemt punkt.

For deres del Glidende vektorer De er utstyrsutstyr til en gitt vektor, men søknadspunktet deres må være inneholdt i vektorhandlingslinjen.

Og Motsatte vektorer De er vektorer som har samme størrelse og retning, men motsatte sanser, selv om de i engelske tekster kalles Motsatte adresser Siden adressen også indikerer betydningen. Motsatte vektorer er ikke utstyr.

Øvelser

-Oppgave 1

Hvilke andre vektorer av de som er vist i figur 1 er utstyr med hverandre?

Løsning

Bortsett fra de som allerede er angitt i forrige seksjon, observeres det fra figur 1 at Annonse, Være og Ec De er også utstyrsvektorer med hverandre:

AD ∼ Be ∼ Ce 

Noen av dem er en representant for klassen med gratis vektorer v.

Vektorer er også utstyr imellom Ae og Bf :

Ae ∼ Bf 

Som er klassrepresentanter W.

-Oppgave 2

Punktene A, B og C er på kartesiske XY -plan, og deres koordinater er:

Kan tjene deg: ideell gass: modell, oppførsel, eksempler

A = (-4.1), b = (-1.4) og c = (-4, -3)

Finn koordinatene til et fjerde punkt D slik at vektorene AB og CD Være utstyr.

Løsning 

Så det CD være utstyr AB må ha samme modul og samme retning som AB .

Modulen til AB Square er:

|AB|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D -koordinater er ukjent for hva vi kan si: D = (x, y)

Da: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Som |AB| = |CD| Det er en av forholdene for AB og CD Være utstyr du har:

(x + 4)^2 + (y + 3)^2 = 18

Siden det er to ukjente, er det nødvendig med en annen ligning, som kan oppnås fra betingelsen som AB og CD være parallell og i samme forstand.

Vektor ab helling

Vektorhellingen AB Angir adressen din:

I påvente av AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Som indikerer at vektoren AB 45º Form med x -aksen.

CD -vektorhelling

Skråningen av CD Det beregnes på samme måte:

I påvente av CD = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Samsvarer med dette resultatet med skråningen av AB Du har følgende ligning:

Y + 3 = x + 4 

Som betyr y = x + 1.

Hvis dette resultatet erstattes i ligningen av likheten mellom modulene, er det:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Forenkling er:

2 (x+4)^2 = 18, 

Som tilsvarer:

(x+4)^2 = 9

Det er x+4 = 3 som innebærer at x = -1. Slik at koordinatene til D er (-1, 0).

Sjekk

Vektorkomponenter AB De er (-1-(-4); 4 -1) = (3; 3)

Kan tjene deg: Thévenin Theorem: Det som består av applikasjoner og eksempler

og de av vektoren CD De er (-1-(-4)); 0 -(-3)) = (3; 3)

Noe som betyr at vektorer er utstyr. Hvis to vektorer har de samme kartesiske komponentene har samme modul og retning, er de derfor utstyr.

-Øvelse 3

Den frie vektoren eller har størrelsesorden 5 og adresse 143.1301º.

Finn sine kartesiske komponenter og bestem koordinatene til punktene B og C, vel vitende om at faste vektorer AB og CD er utstyr. Koordinatene til A er (0, 0) og koordinatene til punkt C er (-3,2).

Løsning 

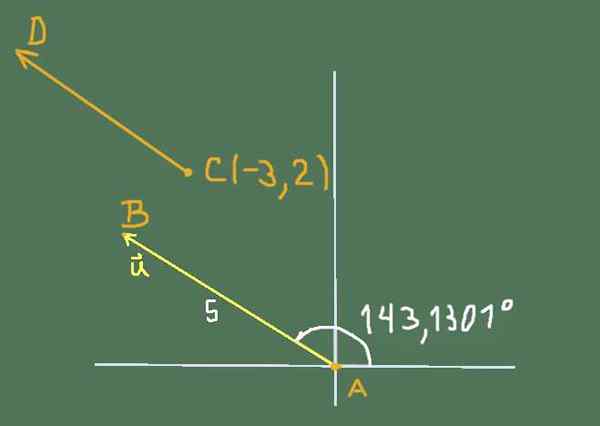
Situasjonen foreslått av øvelsen kan representeres av følgende figur:

Figur 2. Diagram for oppløsning av trening 3. Kilde: Selvlaget.

Kartesiske komponenter av eller er

eller = (5*cos (143,1301º); 5*sin (143,1301º))) 

Å gjøre beregningene gjenstår:

eller = (-4; 3) 

B -koordinater er ukjente, så vi plasserer B (x, y)

Vektorens koordinater AB De er (x-0; y-0), men ettersom det er utstyr med u må oppfylles likheten av komponenter, konkluderes det derfor med at koordinatene til B er (-4, 3).

Tilsvarende vektorkoordinatene CD De er (x-(-3)); (og - 2) Det må være utstyr u, leller det fører til:

 x + 3 = -4 og y -2 = 3

Da vil koordinatene til punkt D være (-7, 5).

Referanser

1. Beregning.DC. Fast vektor. Gratis vektor. Gjenopprettet fra: Beregning.DC
2. 2d Descartes. Faste vektorer og frie vektorer av planet. Hentet fra: Ressurser.utdanning.er
3. Guao Project. Utstyrsvektorer. Gjenopprettet fra: Guao.org
4. Resnick, r., Krane, k. (2001). Fysikk (på engelsk). New York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Fysikk for forskere og ingeniører (på engelsk) (6. utgave). Brooks/Cole.
6. Tupler, Paul a. (2000). Fysikk for vitenskap og teknologi. Volum I. Barcelona: red. Jeg snudde meg.
7. Weisstein, e. "Vektor". I Weisstein, Eric w. Mathworld (på engelsk). Wolfram Research.