Øyeblikkelig hastighetsdefinisjon, formel, beregning og øvelser

De øyeblikkelig hastighet Det er definert som øyeblikkelig forskyvningsendring over tid. Det er et konsept som gir stor presisjon til studiet av bevegelse. Og det er et fremskritt med hensyn til gjennomsnittshastigheten, hvis informasjon er veldig generell.

For å få øyeblikkelig hastighet, la oss se på et tidsintervall så lite som mulig. Differensialberegning er det perfekte verktøyet for å uttrykke denne ideen matematisk.

Øyeblikkelig hastighet står for mobilhastighet på hvert punkt i ruten. Kilde: Pixabay.

Utgangspunktet er gjennomsnittshastigheten:

La oss nå få til å tilnærme seg 0 alt som kan. Dette er en grense og resultatet vil være nettopp øyeblikkelig hastighet:

Denne grensen er kjent med derivatets navn. I notasjonen om differensialberegning har du:

Forutsatt at bevegelsen er begrenset til en rett linje, kan den dispenseres med vektornotasjonen.

[TOC]

Instant hastighetsberegning: Geometrisk tolkning

Følgende figur viser den geometriske tolkningen av konseptet derivat: det er skråningen på linjen tangent Til kurven x (t) vs. t På hvert punkt.

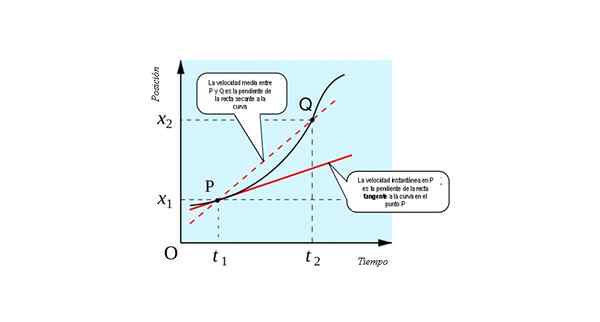Den øyeblikkelige hastigheten i P tilsvarer numerisk med skråningen av linjetangenten til kurven X Vs. t på punkt p. Kilde: Kilde: すじにく シチュー [CC0].

Du kan forestille deg hvordan du får grensen hvis punktet Q gradvis nærmer seg. Det vil komme en tid hvor begge punktene er så nærme, at man ikke kan skilles fra den andre.

Linjen som forener dem, vil da tørke (rett som skjærer seg inn i to punkter) for å være tangent (rett som berører kurven på et enkelt punkt). Derfor, for å finne den øyeblikkelige hastigheten til en mobil partikkel vi bør ha:

• Grafen over partikkelenes plassering som en funksjon av tid. Finne skråningen på linjen Tangens til kurven i hvert øyeblikk av tid, har du øyeblikkelig hastighet på hvert punkt okkupert av partikkelen.

Kan tjene deg: Ampère lov: formel og ligninger, demonstrasjon, øvelser

O vel:

• Partikkelposisjonsfunksjonen x (t), som er avledet for å oppnå hastighetsfunksjonen V (t), da evalueres denne funksjonen hver gang t, En bekvemmelighet. Posisjonsfunksjonen er ment å være avledbar.

Noen spesielle tilfeller i beregningen av øyeblikkelig hastighet

-Hellingen på linjen tangent til kurven i P er 0. En nullhelling betyr at mobilen stoppes og at hastigheten selvfølgelig er 0.

-Hellingen på linjens tangent til kurven i P er større enn 0. Hastigheten er positiv. I grafen ovenfor betyr det at mobilen beveger seg bort fra eller.

-Hellingen på linjen tangent til kurven i P er mindre enn 0. Hastigheten ville være negativ. I grafen ovenfor er det ingen punkter som det, men i så fall vil partikkelen nærme seg eller.

-Hellingen på linjen tangent til kurven er konstant i P og alle andre punkter. I dette tilfellet er grafen en rett linje og mobilen har Ensartet linjebevegelse MRU (hastigheten er konstant).

Generelt sett funksjonen V (t) Det er også en tidsfunksjon, som igjen kan ha avledet. Hva om det ikke var mulig å finne de som ble avledet fra funksjonene x (t) og V (t)?

I tilfelle av x (t) Det kan være at skråningen - den øyeblikkelige hastigheten - endret skilt skarpt. Eller det vil gå fra null til en annen verdi umiddelbart.

I så fall grafikken x (t) Det ville presentere tips eller hjørner ved de plutselige endringene. Veldig forskjellig fra saken representert i forrige bilde, der kurven x (t) Det er en myk kurve, uten punkter, hjørner, diskontinuiteter eller brå endringer.

Kan tjene deg: bose einstein kondensat

Sannheten er at for ekte mobiler er myke kurver de som best representerer objektets oppførsel.

Den generelle bevegelsen er ganske kompleks. Mobil kan stoppes en stund, akselerere for å bevege seg fra hvile for å ha en hastighet og komme seg bort fra utgangspunktet, holde fart en stund, og stopp deretter for å stoppe igjen og dermed stilen.

De kan starte på nytt og fortsette i samme retning. Eller handle tilbakeslag og retur. Dette kalles en variert bevegelse i en dimensjon.

Under noen eksempler på beregning av øyeblikkelig hastighet vil avklare bruken av de gitte definisjonene:

Løst øyeblikkelig hastighetsøvelser

Oppgave 1

En partikkel beveger seg langs en rett linje med følgende bevegelseslov:

x (t) = -t³ + 2 t² + 6 T - 10

Alle enhetene er i internasjonalt system. Finne:

a) Partikkelens plassering på t = 3 sekunder.

b) Gjennomsnittshastigheten i intervallet mellom t = 0 s og t = 3 s.

c) Gjennomsnittshastigheten i intervallet mellom t = 0 s og t = 3 s.

d) den øyeblikkelige hastigheten til partikkelen til det forrige spørsmålet, ved t = 1 s.

Svar

a) For å finne partikkelens plassering, bevegelsesloven (posisjonsfunksjon) ved t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Det er ikke noe problem at stillingen er negativ. Tegnet (-) indikerer at partikkelen er til venstre for opprinnelsen eller.

b) I beregningen av gjennomsnittshastigheten er de endelige og startposisjonene til partikkelen påkrevd i de angitte tider: x (3) og x (0). Posisjonen ved t = 3 er x (3) og er kjent om forrige resultat. Posisjonen på t = 0 sekunder er x (0) = -10 m.

Kan tjene deg: statisk: historie, hvilke studier, applikasjoner, lover

Ettersom den endelige posisjonen er den samme som den første, konkluderes det umiddelbart at gjennomsnittshastigheten er 0.

c) Gjennomsnittshastigheten er årsaken mellom avstanden og tiden brukt. Nå er avstanden modulen eller størrelsen på forskyvningen, derfor:

Avstand = | x2 - x1 | = | -10-(-10) | M = 20 m

Merk at avstanden som reiste alltid er positiv.

v_{m = 20 m/3 s = 6.7 m/s}

d) Her er det nødvendig å finne det første derivatet av stillingen angående tid. Deretter blir det evaluert for t = 1 sekund.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Oppgave 2

Nedenfor er grafen til posisjonen til en mobil som en funksjon av tid. Finn øyeblikkelig hastighet på t = 2 sekunder.

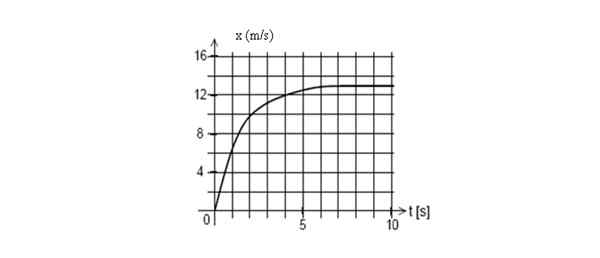Posisjon graf kontra tid for en mobil. Kilde: Selvlaget.

Svar

Tegn tangentlinjen til kurven på t = 2 sekunder, og beregner deretter skråningen, og tar to punkter på linjen.

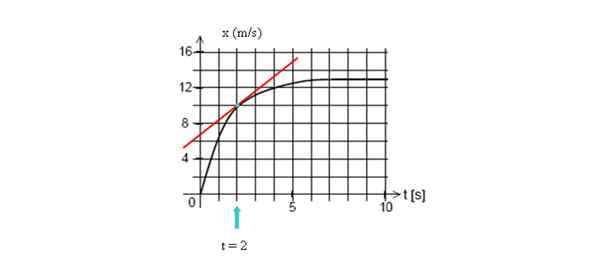For å beregne øyeblikkelig hastighet på det angitte punktet, tegner du tangentlinjen til det punktet og finner skråningen. Kilde: Selvlaget.

I dette eksemplet vil vi ta to punkter som lett blir visualisert, hvis koordinater er (2 s, 10 m) og kuttet med den vertikale aksen (0 s, 7 m):

Referanser

1. Giancoli, d. Fysikk. Prinsipper med applikasjoner. 6^th Utgave. Prentice Hall. 22-25.
2. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 21-22.
3. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7^ma. Utgave. Mexico. Cengage Learning Editors. 23-25.