Gjennomsnittlig akselerasjon hvordan beregnet og løste øvelser

De Gjennomsnittlig akselerasjon til_m Det er størrelsen som beskriver variasjonen av hastigheten på en partikkel i løpet av tiden. Det er viktig, fordi det viser variasjonene som bevegelsen opplever.

For å uttrykke denne størrelsesorden i matematiske termer, er det nødvendig å vurdere to hastigheter og to øyeblikk av tid, som henholdsvis er betegnet som V₁ og v₂, og T₁ og T₂.

Den gjennomsnittlige akselerasjonen er en veldig viktig filmparameter. Kilde: Pixabay.

Ved å kombinere verdiene i henhold til definisjonen som tilbys, vil følgende uttrykk bli tatt:

I det internasjonale systemet hvis enhetene for en_m vil være m/s², Selv om andre enheter som involverer lengde per kvadrat enhet vil tjene.

For eksempel er km/t.s som leser "kilometer i timen og for det andre". Merk at tids enheten vises to ganger. Når du tenker på en mobil som beveger seg langs en rett linje, betyr det at mobilen for hvert sekund øker hastigheten med 1 km/t. Eller avtar med 1 km/t i hvert sekund som passerer.

[TOC]

Akselerasjon, hastighet og hastighet

Selv om det er assosiert med akselerasjon med en økning i hastighet, er sannheten at det nøye observerer definisjonen, viser det seg at enhver hastighetsendring innebærer eksistensen av en akselerasjon.

Og hastigheten endres ikke alltid i størrelsesorden. Det kan hende at mobilen bare varierer fra retning og holder hastigheten konstant. Fortsatt er det en akselerasjon som er ansvarlig for denne endringen.

Et eksempel på dette er en bil som gir en kurve med konstant hastighet på 60 km/t. Kjøretøyet er underlagt en akselerasjon, som er ansvarlig for å endre hastighetsretningen slik at bilen følger kurven. Sjåføren bruker det ved å bruke rattet.

Slik akselerasjon er rettet mot midten av den buede banen, for å få bilen til å ikke komme ut av den. Motta akselerasjonsnavn radial enten normal. Hvis den radielle akselerasjonen plutselig ble annullert, kunne ikke bilen lenger gi kurven og fortsette i en rett linje.

Kan tjene deg: Wimshurst Machine: History, How It Works and Applications

En bil som beveger seg gjennom en kurve er et eksempel på to -dimensjonal bevegelse, mens når den marsjerer i en rett linje, er bevegelsen en -dimensjonal. I dette tilfellet er den eneste effekten av akselerasjon å endre hastigheten på bilen.

Denne akselerasjonen kalles akselerasjon tangensiell. Det er ikke eksklusivt for den endimensjonale bevegelsen. Bilen som gir kurven ved 60 km/t kan samtidig akselerere 70 km/t mens du tar den. I dette tilfellet må sjåføren bruke både rattet og gasspedalen.

Hvis vi vurderer en endimensjonal bevegelse, har den gjennomsnittlige akselerasjonen en geometrisk tolkning som ligner på gjennomsnittshastigheten, som en skråning av tørkelinjen som kutter kurven i punktene P og Q på hastighetsgrafen kontra tid.

Dette kan sees i følgende figur:

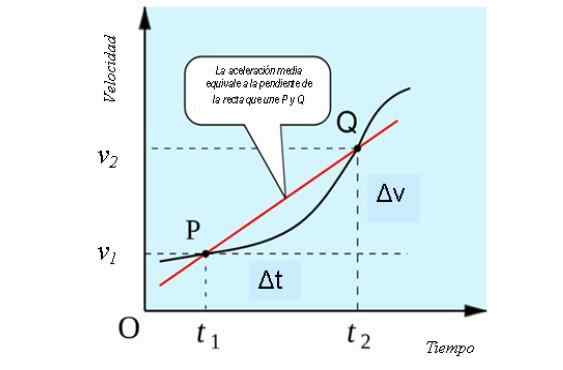Geometrisk tolkning av gjennomsnittlig akselerasjon. Kilde: Kilde: すじにく シチュー [CC0].

Hvordan den gjennomsnittlige akselerasjonen beregnes

La oss se på noen eksempler for å beregne gjennomsnittlig akselerasjon i forskjellige situasjoner:

I) På et bestemt øyeblikk av tid har en mobil som beveger seg langs en rett linje en hastighet på + 25 km/t og 120 sekunder senere har en annen på -10 km/t. Hva var den gjennomsnittlige akselerasjonen?

Svar

Ettersom bevegelsen er en -dimensjonal, kan vektortrasjonen dispenseres med, i hvilket tilfelle:

v_enten = +25 km/h = +6.94 m/s

v_F = -10 km/h = - 2.78 m/s

Δt = 120 s

Hver gang du har en øvelse med blandede størrelser som dette, der det er timer og sekunder, er det nødvendig å overføre alle verdiene til de samme enhetene.

Å være en endimensjonal bevegelse, har vektornotasjonen blitt dispensert med.

Ii) En syklist beveger seg østover med en hastighet på 2.6 m/s og 5 minutter senere går sørover til 1.8 m/s. Finn den gjennomsnittlige akselerasjonen.

Det kan tjene deg: Vy Canis Majoris: oppdagelse, egenskaper, struktur, trening og evolusjon

Svar

Bevegelsen er ikke en -dimensjonal, derfor brukes vektornotasjonen. Enhetsvektorene Yo og J De indikerer adressene ved siden av følgende tegnkonvensjon, og letter beregningen:

• Nord: +J
• Sør: -J
• Dette: +Yo
• Vest: -Yo

v₂ = - 1.8 J m/s

v₁ = + 2.6 Yo m/s

Δt = 5 minutter = 300 sekunder

Akselerasjonsskiltet i den endimensjonale bevegelsen

Som alltid hva som skjer med gjennomsnittlig eller gjennomsnittlig størrelsesorden, er informasjonen som er gitt global. De tilbyr ikke detaljer om hva som skjedde med mobilen i hvert øyeblikk av tid, men det de bidrar er fortsatt verdifullt for beskrivelsen av bevegelsen.

Gjennom begge tegn på hastighet og akselerasjon er det mulig å vite om en mobil som beveger seg på en linje akselererer eller bremser. I begge situasjoner er akselerasjonen til stede, siden hastigheten endrer seg.

Dette er noen interessante betraktninger angående tegn på disse to størrelsene:

• Gjennomsnittlig hastighet og akselerasjon, begge av samme tegn, betyr at mobilen blir raskere og raskere og raskere.
• Hastighet og akselerasjon med forskjellige tegn er et tegn på en mobil har signert.

Det er vanligvis tenkt at når det er en negativ akselerasjon, bremser mobilen. Dette er sant hvis mobilhastigheten er positiv. Men hvis det er negativt, øker faktisk hastigheten.

Som alltid når bevegelsen blir studert, tenkes spesielle tilfeller. For eksempel hva som skjer når den gjennomsnittlige akselerasjonen er null?. Betyr det at mobilen alltid har opprettholdt sin konstante hastighet?

Svaret er nei. Mobilen kunne ha variert hastigheten i intervallet som ble vurdert, men den første hastigheten og finalen var den samme. For øyeblikket er detaljene om hva som skjedde i intervallet ukjent, siden den gjennomsnittlige akselerasjonen ikke gir mer informasjon.

Kan tjene deg: Joule Effekt: Forklaring, eksempler, øvelser, applikasjoner

Hva om den gjennomsnittlige akselerasjonen til_m Det er lik akselerasjon til Når som helst i det midlertidige intervallet? Dette er en veldig interessant situasjon som kalles rettlinjet bevegelse enhetlig variert eller MRUV).

Betyr at hastigheten endres jevnt over tid. Derfor er akselerasjonen konstant. I naturen er det en slik bevegelse, som alle er kjent med: fritt fall.

Fritt fall: En bevegelse med konstant akselerasjon

Det er et kjent faktum at jorden tiltrekker seg gjenstander mot sitt sentrum, og at ved å frigjøre noen i en viss høyde, opplever den akselerasjonen av tyngdekraften, hvis verdi er omtrent konstant og lik 9.8 m/s² nær overflaten.

Hvis luftmotstand ikke griper inn, er bevegelsen vertikal og er kjent som fritt fall. Når akselerasjonen er konstant og velger t₀ = 0, den gjennomsnittlige akselerasjonsligningen transformeres til:

Der det oppnås en kjent formel for å finne hastigheten i hvert øyeblikk av høsten:

v_F = v₀ + AT = GT (V₀= 0)

Hvor a = g = 9.8 m/s²

Trening løst

Et objekt slippes fra nok høyde. Finn hastigheten etter 1.25 sekund.

Svar

v_enten = 0, siden objektet er droppet, da:

v_F = GT = 9.8 x 1.25 m/s = 12.25 m/s, rettet vertikalt mot bakken. (Den vertikale retningen er tatt ned som positiv).

Når objektet nærmer seg bakken, øker hastigheten med 9.8 m/s for hvert sekund går. Massen til objektet er ikke involvert. To forskjellige gjenstander, falt fra samme høyde og samtidig utvikler samme hastighet som de faller.

Referanser

1. Giancoli, d. Fysikk. Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 21-35.
2. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 20-34.
3. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7^ma. Utgave. Mexico. Cengage Learning Editors. 21-39.