Antiderivative formler og ligninger, eksempler, øvelser

EN Antiderivat F (x) av en funksjon F(x) kalles også primitiv eller ganske enkelt den ubestemte integralen av nevnte funksjon, hvis i et gitt intervall Yo, Det er sant, det F '(x) = f (x)

La oss for eksempel ta følgende funksjon:

f (x) = 4x³

Et antiderivat av denne funksjonen er f (x) = x⁴, siden ved å utlede f (x) av avledningsregelen for kreftene:

Det oppnås nøyaktig f (x) = 4x³.

Imidlertid er dette bare en av de mange antiderivativene til F (x), siden denne andre funksjonen: g (x) = x⁴ + 2 Det er også, fordi ved å utlede g (x) med hensyn til x, er det den samme oppnås tilbake f (x).

La oss sjekke det:

Husk at den som er avledet fra en konstant er 0. Derfor til begrepet x⁴ Du kan legge til hvilken som helst konstant, og dets derivat vil fortsette å være 4x³.

Det konkluderes med at enhver funksjon av den generelle formen f (x) = x⁴ + C, der C er en virkelig konstant, fungerer som antiderivat av F (x).

Det forrige illustrerende eksemplet kan uttrykkes som følger:

df (x) = 4x³ Dx

Det udefinerte antiderivatet eller integralen uttrykkes med symbolet ∫, derfor:

F (x) = ∫4x³ dx = x⁴ + C

Der funksjonen f (x) = 4x³  Det kalles Integrering, og C er Integrasjonskonstant.

[TOC]

Eksempler på antiderivativer

Figur 1. Anti -Hotley er ikke annet enn en ubestemt integrert. Kilde: Pixabay.

Å finne et antiderivat av en funksjon er enkel i noen tilfeller der derivatene er velkjente. Vær for eksempel funksjonen f (x) = sen x, en uniderivert for det er en annen funksjon f (x), slik at når den avledes oppnås f (x).

Den funksjonen kan være:

F (x) = - cos x

La oss sjekke at det er sant:

F '(x) = (- cos x)' =- (-sen x) = sin x

Derfor kan vi skrive:

∫sen x dx = -cos x + c

I tillegg til å kjenne derivatene, er det grunnleggende og enkle integrasjonsregler for å finne ubestemt antiderivat eller integrert.

Kan tjene deg: påfølgende derivater

Være en virkelig konstant, da:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Hvis en H (x) -funksjon kan uttrykkes som sum eller subtraksjon av to funksjoner, er dens ubestemte integral:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Dette er linearitetens egenskap.

De Maktregel For integraler kan det etableres på denne måten:

Denne regelen har en åpenbar begrensning: Siden nevneren N +1 Det kan ikke gjøres 0, derfor n ≠ -1.

I tilfelle av n = -1 brukes følgende regel:

5.- ∫x ^-1 Dx = ln x +c

Det er lett å demonstrere at derivatet av ln x Det er nettopp x ^-1.

Differensiallikninger

En differensialligning er en der det ukjente er som et derivat.

Nå, fra forrige analyse, er det lett å innse at den omvendte operasjonen til derivatet er det udefinerte antiderivatet eller integralen.

La f (x) = y '(x), det vil si avledet fra en viss funksjon. Vi kan bruke følgende notasjon for å indikere dette derivatet:

Det følger umiddelbart det:

dy = f (x) dx

Det ukjente av differensialligningen er funksjonen y (x), den derivatet er f (x). For å fjerne det er det forrige uttrykket integrert på begge sider, noe som tilsvarer å bruke antiderivatet:

∫dy = ∫f (x) dx

Den venstre integralen løses ved integrasjonsregel 1, med k = 1 og dermed blir den etterspurte -awaitten ryddet:

og (x) = ∫f (x) dx = f (x) + c

Og siden C er en virkelig konstant, å vite hvilken som er passende i hvert tilfelle, må uttalelsen inneholde tilstrekkelig tilleggsinformasjon til å beregne verdien av C. Dette kalles Innledende tilstand.

Vi vil se eksempler på anvendelse av alt dette i neste avsnitt.

Kan tjene deg: punktlig estimat

Antideriverte øvelser

- Oppgave 1

Bruk integrasjonsreglene for å få følgende udefinerte antiderivater eller integraler av funksjonene som er gitt, forenkle resultatene så mye som mulig. Det er praktisk å bekrefte resultatet ved avledning.

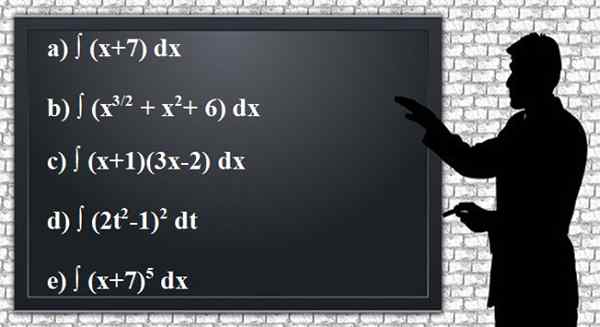Figur 2. Definerte anteriverte eller integrerte øvelser. Kilde: Pixabay.

Løsning på

Vi bruker først regel 3, siden integreringen er summen av to vilkår:

∫ (x +7) dx = ∫ xdx +∫7dx

For den første integreringen brukes styrets regel:

∫ xdx = (x² /2)+C₁

I den andre integrerte regel 1 gjelder det å være k = 7:

∫7dx = 7∫dx = 7x + c₂

Og nå blir resultatene lagt til. De to konstantene er gruppert i en, generisk kalt C:

∫ (x+7) dx = (x² /2) + 7x + C

Løsning b

Ved linearitet dekomponerer denne integralen i tre enklere integraler, som maktens styre vil bli brukt til:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Legg merke til at for hver integral vises en integrasjonskonstant, men de møtes i en enkelt samtale C.

Løsning c

I dette tilfellet er det praktisk å anvende distribusjonens distribusjonsegenskaper for å utvikle integreringen. Deretter bruker du maktens regel for å finne hver integral separat, som i året før.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Den imøtekommende leseren vil observere at de to sentrale begrepene er like, derfor reduseres de før de integrerer:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Løsning e

En måte å løse integralen på ville være å utvikle kraft, som det ble gjort i eksempel D. Ettersom eksponenten er høyere, ville det imidlertid være nødvendig å gjøre en variabel endring, for ikke å måtte gjøre en så lang utvikling.

Kan tjene deg: kontinuerlig tilfeldig variabel

Den variable endringen er som følger:

U = x + 7

Avleder på begge sider dette uttrykket:

du = dx

Integralen transformeres til en enklere med den nye variabelen, som er løst med maktens regel:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Til slutt blir endringen returnert for å gå tilbake til den opprinnelige variabelen:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Oppgave 2

En partikkel er opprinnelig i ro og beveger seg langs x -aksen. Dens akselerasjon for t> 0 er gitt ved funksjon a (t) = cos t. Det er kjent at ved t = 0 er posisjonen x = 3, alle i enhetene i det internasjonale systemet. Det blir bedt om å finne hastigheten V (t) og posisjon X (t) i partikkelen.

Løsning

Siden akselerasjon er den første avledet fra hastighet med hensyn til tid, har du følgende differensialligning:

a (t) = v '(t) = cos t

Det følger at:

v (t) = ∫ cos t dt = sin t + c₁

På den annen side vet vi at hastigheten igjen er derivatet av posisjonen, derfor integrerer vi igjen:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Integrasjonskonstanter bestemmes ut fra informasjonen som er gitt i uttalelsen. Først sier han at partikkelen opprinnelig var i ro, derfor V (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Da må du x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + C₂ = 3 → C₂ = 3+1 = 4

Hastighets- og posisjonsfunksjoner er definitivt slik:

v (t) = sen t

x (t) = - cos t + 4

Referanser

1. Engler, a. 2019. Integrert beregning. National University of the Coast.
2. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
3. Gratis matematikkekster. Antiderivativer. Gjenopprettet fra: Matematikk.Liibretexts.org.
4. Wikipedia. Antiderivat. Hentet fra: i.Wikipedia.org.
5. Wikipedia. Ubestemt integrasjon. Gjenopprettet fra: er.Wikipedia.org.