Boltzmann konstant historie, ligninger, beregning, øvelser

De Boltzmann konstant Det er verdien som relaterer den gjennomsnittlige kinetiske energien til et termodynamisk system eller et objekt med den absolutte temperaturen på det samme. Selv om de ofte er forvirrede, er ikke temperatur og energi det samme konseptet.

Temperaturen er et mål på energi, men ikke selve energien. Med Boltzmann konstant er en knyttet til hverandre som følger:

OG_c = (3/2) k_B  T

Boltzmann vert i Wien. Kilde: Dadotet på engelsk Wikipedia [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Denne ligningen er gyldig for et ideelt monoatomisk gassmolekyl m, hvor OG_c Det er hans kinetiske energi gitt i Joules, K_B Det er Boltzmanns konstante og T Det er den absolutte temperaturen i Kelvin.

På denne måten, når temperaturen øker, øker også den gjennomsnittlige kinetiske energien med stoffmolekylet, som forventet å skje. Og det motsatte skjer når temperaturen avtar, og kan nå det punktet hvor hele bevegelsen opphører, den laveste mulige eller absolutte temperaturen er nådd.

Når du snakker om gjennomsnittlig kinetisk energi, er det nødvendig å huske at kinetisk energi er assosiert med bevegelse. Og partiklene kan bevege seg på mange måter, for eksempel å bevege, rotere eller vibrere. Selvfølgelig vil ikke alle gjøre det på samme måte, og ettersom de er utallige, blir gjennomsnittet tatt for å karakterisere systemet.

Noen energilater er mer sannsynlig enn andre. Dette konseptet er av radikal betydning i termodynamikk. Energien som vurderes i den forrige ligningen er kinetisk oversettelse av kinetisk energi. Av sannsynligheten for statene og deres forhold til Boltzmann Constant vil snakke litt senere.

I 2018 ble Kelvin omdefinert og med ham Boltzmann -konstanten, som i det internasjonale systemet er omtrent 1.380649 x 10^-23 J. K^-1. Mye mer presisjon kan oppnås for Boltzmann -konstanten, som er blitt bestemt i mange laboratorier over hele verden, ved forskjellige metoder.

[TOC]

Historie

Den berømte konstanten skylder navnet til fysikeren Ludwig Boltzmann (1844-1906), født i Wien, som dedikerte livet sitt som vitenskapsmann til studiet av den statistiske oppførselen til systemene med mange partikler, fra synspunktet til Newtonian Mechanics.

Selv om atomets eksistens i dag er universelt akseptert, i det nittende århundre troen på om atomet virkelig eksisterte eller var en gjenstand som mange fysiske fenomener ble forklart var i full debatt.

Kan tjene deg: normal vektor: beregning og eksempel

Boltzmann var en sterk forsvarer av atomets eksistens, og i sin tid møtte han hard kritikk av sitt arbeid av mange kolleger, som vurderte at de inneholdt uoppløselige paradokser.

Han erklærte at observerbare fenomener på makroskopiske nivåer kunne forklares gjennom de statistiske egenskapene til bestanddeler som atomer og molekyler.

Denne kritikken kan skyldes den dype episoden med depresjon som førte til at han tok sitt eget liv i begynnelsen av september 1906, da han fortsatt hadde mye å gjøre, fordi han ble ansett som en av de store teoretiske fysikerne i sin tid og der var lite med at andre forskere vil bidra til å bekrefte sannheten i teoriene deres.

Det skjedde ikke lenge etter hans død da nye funn om atomets natur og hans konstituerende partikler ville bli lagt til for å gi grunnen til Boltzmann.

Boltzmanns konstante og Plancks verk

Nå, Boltzmann er konstant k_B Det ble introdusert som det er kjent i dag en stund etter arbeidet til den østerrikske fysikeren. Det var Max Planck, i hans lov om utslippet av den svarte kroppen, et verk han presenterte i 1901, som på den tiden ga ham verdien av 1,34 x 10²³ J/k.

I løpet av 1933 ble Boltzmann lagt til Wien som en plakat hyllest en plakett med definisjonen av entropi som involverer den berømte konstanten: S = k_B Logg w, ligning som vil bli diskutert senere.

I dag er Boltzmanns konstant uunnværlig i anvendelsen av de termodynamiske lovene, statistisk mekanikk og informasjonsteori, hvor denne fysikeren med trist slutt var en pioner.

Verdi og ligninger

Gasser kan beskrives i makroskopiske termer og også i mikroskopiske termer. For den første beskrivelsen er det konsepter som tetthet, temperatur og trykk.

Det må imidlertid huskes at en gass er sammensatt av mange partikler, som har en global tendens til en viss oppførsel. Det er den trenden som er makroskopisk målt. En måte å bestemme Boltzmanns konstante er takket være den velkjente ligningen av ideelle gasser:

p.V = n. R. T

Her p Det er gasstrykk, V Det er volumet, n Det er antall føflekker til stede, R Det er gassens konstant og T Det er temperaturen. I en mol med ideell gass blir følgende forhold mellom produktet oppfylt p.V, og oversettelsens kinetiske energi K Hele settet er:

Kan tjene deg: Corpuscular Model of Matter

p.V = (2/3). K

Derfor er kinetisk energi:

K = (3/2) n.R.T

Ved å dele med det totale antallet molekyler til stede, som vil bli kalt n, oppnås den gjennomsnittlige kinetiske energien til en enkelt partikkel:

OG_c = K /n

OG_c= (3/2n) n.R.T

I en mol er det antall partikler n_TIL, Og derfor er det totale antall partikler N = nnA, opphold:

OG_c = (3/2nn_TIL) n.R.T

Nettopp kvotienten R/n_TIL Det er Boltzmanns konstante, og blir demonstrert at den kinetiske energien til gjennomsnittlig oversettelse av en partikkel bare avhenger av den absolutte temperaturen og ikke andre størrelser som trykk, volum eller til og med typen molekyl:

OG_c = (3/2) k_B. T

Boltzmanns konstante og entropi

En gass har en gitt temperatur, men at temperaturen kan samsvare med forskjellige indre energiletilstander. Hvordan visualisere denne forskjellen?

Tenk på samtidig lansering av 4 mynter og måtene de kan falle:

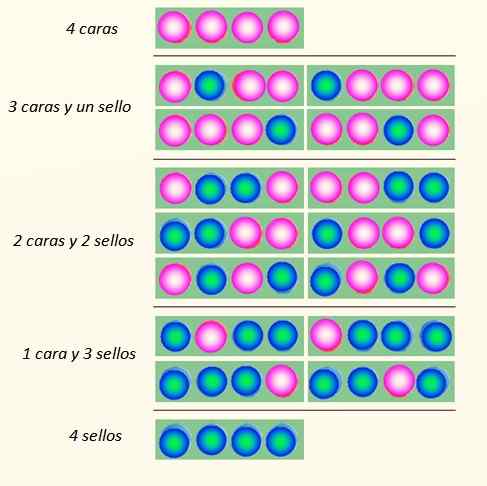Måter 4 mynter kan falle. Kilde: Selvlaget

Myntsettet kan anta totalt 5 stater, som blir vurdert Makroskopisk, beskrevet på figuren. Hvilke av disse statene vil leseren si at det er mest sannsynlig?

Svaret skal være tilstanden til 2 ansikter og 2 kors, fordi det har totalt 6 muligheter, av de 16 illustrert på figuren. Og 2⁴ = 16. Disse tilsvarer statene mikroskopisk.

Og hva hvis 20 mynter lanseres i stedet for 4? Det ville være totalt 2^tjue muligheter eller "mikroskopiske tilstander". Det er et mye større og vanskeligere antall å håndtere. For å lette behandlingen av stort antall, er logaritmer veldig passende.

Det som virker tydelig er at staten med den største lidelsen er mest sannsynlig. De mest bestilte statene som 4 ansikter eller 4 frimerker er litt mindre sannsynlige.

Entropien til en makroskopisk tilstand er definert som:

S = k_B ln w

Hvor W Det er antall mulige mikroskopiske tilstander og k_B Det er Boltzmanns konstante. Som ln w Det er dimensjonsløst, entropi har de samme enhetene som k_B: Joule/K.

Dette er den berømte ligningen i Boltzmanns gravstein i Wien. Imidlertid er mer enn entropi, det aktuelle er endringen av det:

Det kan tjene deg: Termodynamiske variabler: som er og øvelser løst

ΔS = k_B ln w₂ - k_B ln w₁ = k_B ln (w₂/w₁)

Hvordan beregnes K_B?

Verdien av Boltzmann -konstanten oppnås eksperimentelt presist med målinger basert på Akustisk termometri, som utføres ved hjelp av eiendommen som etablerer avhengigheten av lydhastigheten i en gass med temperaturen på den samme.

Faktisk er lydhastigheten i en gass gitt av:

Hvor b _adiabatisk Det er den adiabatiske komprimerbarhetsmodulen gitt av:

B_adiabatisk = γP

Og ρ er gasstetthet. For den forrige ligningen, p Det er presset fra den aktuelle gassen og γ Det er den adiabatiske koeffisienten, hvis verdi for en spesifikk gass finnes i tabeller.

Metrologiinstitutter opplever også andre måter å måle konstanten på, for eksempel Johnson støytermometri, som bruker de termiske svingningene som oppstår tilfeldig i materialene, spesielt hos drivere.

Løste øvelser

-Oppgave 1

Finne:

a) Den kinetiske energien til gjennomsnittlig oversettelse OG_c som har et ideelt gassmolekyl ved 25 ºC

b) Oversettelsens kinetiske energi K av molekylene i 1 mol av denne gassen

C) Gjennomsnittshastigheten til et oksygenmolekyl ved 25 ºC

Faktum

m_oksygen = 16 x 10 ^-3 kg/mol

Løsning

til) OG_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 k = 6.2 x 10^-tjueen J

b) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/mol .K x 298 k = 3716 j

c) OG_c = ½ mv², Når man tar i betraktning at oksygenmolekylet er diatomisk og molmassen må multipliseres med 2, vil den være:

-Oppgave 2

Finn endring av entropi når 1 mol gass okkupert med et volum på 0.5m³ Det utvides til å okkupere 1 m³.

Løsning

ΔS = k_B ln (w₂/w₁)

W₂= 2^NW₁ (Det var 2⁴ Mikroskopiske tilstander for lanseringen av de 4 myntene, husk?)

Hvor n er antall partikler som er til stede i 0.5 mol gass 0.5 x n_TIL:

ΔS = k_B LN (2^N W₁/w₁) = k_B ln 2^N= k_B 0.5n_TIL ln 2 = 2.88 J/K

Referanser

1. Atkins, p. 1999. Fysisk kjemi. Omega -utgaver. 13-47.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 664-672.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. 647-673.
5. Hvis omdefinering. Kelvin: Boltzmann Constant. Gjenopprettet fra: NIST.Gov