U -test av Mann - Whitney hva som er og når det gjelder, utførelse, eksempel

De U -test av Mann - Whitney Det brukes for å sammenligne to uavhengige prøver når de har få data eller ikke følger en normalfordeling. På denne måten anses det for å være en test ikke parametrisk, I motsetning til motstykket ditt Student t test, som brukes når prøven er stor nok og følger normalfordelingen.

Frank Wilcoxon foreslår det for første gang i 1945, for prøver av identiske størrelser, men to år senere ble det utvidet i tilfelle av prøver av forskjellig størrelse av Henry Mann og D. R. Whitney.

Figur 1. U -testen av Mann - Whitney blir brukt for sammenligning av uavhengige prøver. Kilde: Pixabay.

Ofte brukes testen for å verifisere om det er et forhold mellom en kvalitativ variabel og en annen kvantitativ.

Et illustrerende eksempel er å ta et sett med hypertensive mennesker og trekke ut to grupper, som de daglige blodtrykksdataene er registrert i en måned.

For en gruppe blir behandlingen A og en annen brukt behandlingen B. Her er blodtrykk den kvantitative variabelen og behandlingstypen er den kvalitative.

Du vil vite om medianen, og ikke gjennomsnittet, av de målte verdiene er statistisk like eller annerledes, for å fastslå om det er en forskjell mellom begge behandlingene. For å få svaret blir Wilcoxon eller U -testen av Mann - Whitney brukt.

[TOC]

Problemtilnærming i U -testen av Mann - Whitney

Et annet eksempel der testen kan brukes er som følger:

Anta at du vil vite om forbruket av brus skiller seg betydelig i to regioner i landet.

En av dem heter Region A og den andre regionen B. En oversikt over liter som konsumeres ukentlig i to prøver blir utført: en av 10 personer for region A og en annen av 5 personer for region B.

Dataene er som følger:

-Region A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Region b: 12,14, 11, 30, 10

Følgende spørsmål reises:

Avhenger forbruket av brus (y) av regionen (x)?

Kvalitative variabler kontra kvantitative variabler

-Kvalitativ variabel x: Region

-Kvantitativ variabel og: Gassforbruk

Hvis mengden liter som konsumeres er den samme i begge regioner, vil konklusjonen være at det ikke er noen avhengighet mellom de to variablene. Måten å vite er å sammenligne gjennomsnittlig eller median trend for de to regionene.

Normal sak

Hvis dataene fulgte en normalfordeling, blir to hypoteser hevet: Null H0 og H1 -alternativet gjennom sammenligningen mellom midlene:

Kan tjene deg: bemerkelsesverdige produkter

-H0: Det er ingen forskjell mellom gjennomsnittet av de to regionene.

-H1: Midlene for begge regioner er forskjellige.

Sak med ingen - normal tendens

Tvert imot, hvis dataene ikke følger en normalfordeling eller bare prøven er veldig liten å vite, i stedet for å sammenligne gjennomsnittet, vil den bli sammenlignet Medianen av de to regionene.

-H0: Det er ingen forskjell mellom medianen av de to regionene.

-H1: Medianene i begge regioner er forskjellige.

Hvis medianene sammenfaller, blir nullhypotesen oppfylt: det er ingen sammenheng mellom brusforbruk og regionen.

Og hvis det motsatte skjer, er den alternative hypotesen sann: det er en sammenheng mellom forbruk og region.

Det er for disse tilfellene der U -testen av Mann - Whitney er indikert.

Prøve eller ikke -parrede prøver

Følgende viktige problemstillinger for å avgjøre om Mann Whitneys U -test brukes, er om antallet data i begge prøvene er identisk, noe som tilsvarer å si at de samtidig.

Hvis de to prøvene er sammenkoblet, vil den originale Wilcoxon -versjonen gjelde. Men hvis ikke, som tilfellet med eksemplet, blir den modifiserte Wilcoxon -testen brukt, som er nettopp Mann Whitneys U -test.

Mann whitney u testegenskaper

U -testen av Mann -Whitney En ikke -parametrisk test, gjeldende for prøver som ikke følger normalfordelingen eller med få data. Den har følgende egenskaper:

1.- Sammenlign medianene

2.- Fungerer med bestilte områder

3.- Det er mindre kraftig, forståelse av makt sannsynligheten for å avvise nullhypotesen når det i virkeligheten er falsk.

Når man tar hensyn til disse egenskapene, brukes U -testen av Mann - Whitney når:

-Dataene er uavhengige

-De følger ikke normalfordelingen

-Null H0 -hypotesen aksepteres hvis mediet til de to prøvene sammenfaller: MA = MB

-H1 -alternativ hypotesen aksepteres hvis mediet til de to prøvene er forskjellige: MA ≠ MB

Mann Formula - Whitney

U -variabelen er kontraststatiteten som brukes i Mann - Whitney -testen, og den er definert:

U = min (UA, UB)

Dette betyr at u er det minste av verdiene mellom UA og UB, brukt på hver gruppe. I vårt eksempel ville det være for hver region: a o b.

UA- og UB -variabler er definert og beregnet i henhold til følgende formel:

Ua = nb + na (na +1)/2 - ra

UB = NB + NB (NB +1)/2 - RB

Kan tjene deg: Reduksjon av lignende vilkår

Her er Na- og Nb -verdiene størrelsene på prøvene som tilsvarer henholdsvis region A og B, og på den annen side er RA og RB rekkevidde summer som vi vil definere nedenfor.

Trinn for å bruke testen

1.- Bestill verdiene til de to prøvene.

2.- Tilordne et ordreområde til hver verdi.

3.- Riktig eksisterende ligaturer i dataene (gjentatte verdier).

4.- Beregn Ra = sum av utvalget av prøven a.

5.- Finn RB = summen av utvalget av prøve B.

6.- Bestem UA- og UB -verdien, i henhold til formlene gitt i forrige seksjon.

7.- Sammenlign UA og UB, og den mindreårige av de to er tildelt den eller eksperimentelle statistikken (det vil si dataene) sammenlignet med den teoretiske eller normale statistikken.

Praktisk anvendelse av anvendelse

Nå bruker vi de nevnte problemet med brus som tidligere er hevet:

Region A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Region B: 12,14, 11, 30, 10

Avhengig av at midlene til begge prøvene er statistisk de samme eller forskjellige, fortsetter vi med å akseptere eller avvise nullhypotesen: det er ingen sammenheng mellom variabelen og og x, det vil si at forbruket av brus ikke avhenger av regionen:

H0: MA = MB

H1: MA ≠ MB

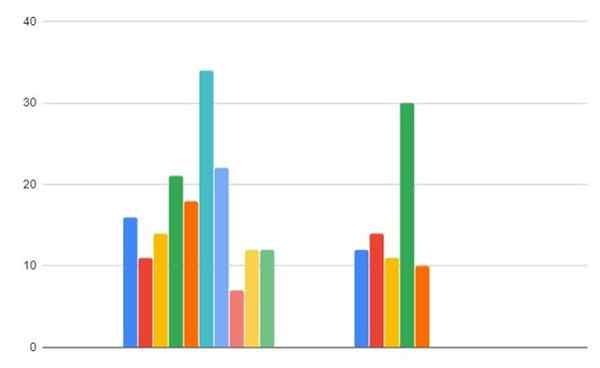Figur 2. Gassforbruksdata i region A og B. Kilde: f. Zapata.

- Trinn 1

Vi fortsetter med å bestille dataene i fellesskap for de to prøvene, og bestiller verdiene fra minst til største:

Merk at verdien 11 vises 2 ganger (en gang i hver prøve). Opprinnelig har den posisjoner eller områder 3 og 4, men ikke for å overvurdere eller undervurdere den ene eller den andre gjennomsnittsverdien er valgt som et område, det vil si 3,5.

Tilsvarende videreføres 12 -verdien, som gjentas tre ganger med områdene 5, 6 og 7.

Vel, verdien 12 er tildelt det gjennomsnittlige området 6 = (5+6+7)/3. Og det samme for verdi 14, som har ligering (vises i begge prøvene) i posisjon 8 og 9, er gjennomsnittlig område 8 tildelt.5 = (8+9)/2.

- Steg 2

Dataene for region A og B blir deretter separert igjen, men nå tildeles deres tilsvarende områder i en annen rad:

Region A

Region b

RB -områder oppnås fra summeret for elementene i den andre raden for hvert tilfelle eller region.

Trinn 3

De respektive UA- og UB -verdiene beregnes:

UA = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Eksperimentell verdi u = min (19, 31) = 19

Trinn 4

Teoretikeren skal visstnok følge en normalfordeling n med parametere gitt utelukkende av størrelsen på prøvene:

Kan tjene deg: irrasjonelle tall: historie, egenskaper, klassifisering, eksempler

N ((Na⋅nb) /2, √ [NB (Na + NB +1) /12])

For å sammenligne variabelen eller eksperimentelt oppnådd, med den teoretiske er det nødvendig å gjøre en variabel endring. Det går fra variabelen eller eksperimentell til verdien karakterisert, som vil bli kalt Z, For å kunne sammenligne med en normalfordeling som er karakterisert.

Den variable endringen er som følger:

Z = (u - na.Nb / 2) / √ [na. NB (Na + NB + 1) / 12] 

Det skal bemerkes at for endring av variabel ble parametrene for den teoretiske distribusjonen for u brukt. Deretter den nye Z -variabelen, som er en hybrid mellom teoretisk og eksperimentell eller en normalfordeling karakterisert N (0,1).

Sammenligningskriterier

Hvis z ≤ zα ⇒ Null H0 -hypotesen er akseptert

Ja Z> Zα ⇒ Null H0 -hypotesen blir avvist

De kritiske verdiene Zα karakterisert avhenger av nivået av tillit som kreves, for eksempel for et tillitsnivå α = 0,95 = 95% som er den mest vanlige har den kritiske verdien Zα = 1,96.

For dataene som er vist her:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0,73

Som er under den kritiske verdien 1.96.

Da er den endelige konklusjonen at nullhypotesen blir akseptert:

Det er ingen forskjell i forbruket av brus mellom regioner A og B.

Online kalkulatorer for U -testen av Mann - Whitney

Det er spesifikke programmer for statistiske beregninger, inkludert SPSS og Minitab, men disse programmene er betalt og bruken av dem er ikke alltid enkelt. Dette er fordi de gir så mange alternativer, at bruken praktisk talt er forbeholdt statistikkeksperter.

Heldigvis er det flere veldig presise, gratis og enkle online programmer som tillater blant annet U -Whitney U -testene.

Disse programmene er:

-Samfunnsvitenskapelig statistikk (Socscistatistics.com), som har både U-Whitney U-test og Wilcoxon for balanserte eller sammenkoblede prøver.

-AI-terapistatistikk (AI-terapi.com), som har flere av de vanlige beskrivende statistiske testene.

-Statistisk å bruke (fysikk.CSBSJU.EDU/statistikk), en av de eldste, så grensesnittet ditt kan se utdatert ut, selv om det er et veldig effektivt gratis program.

Referanser

1. Dietrichson. Kvantitative metoder: Ranges Test. Gjenopprettet fra: Bookdown.org
2. Marín J p. SPSS Guide: Analyse og prosedyrer i ikke -parametriske tester. Gjenopprettet fra: Halweb.UC3M.er
3. Usal MOOC. Ikke -parametrisk test: U of Mann - Whitney. Gjenopprettet fra: YouTube.com
4. Wikipedia. U -test av Mann - Whitney. Gjenopprettet fra: er.Wikipedia.com
5. Xlstat. Hjelpesenter. Mann Test Tutorial - Whitney i Excel. Gjenopprettet fra: Hjelp.Xlsat.com