Generell parabola -ligning (eksempler og øvelser)

De Lignelse generell ligning inneholder kvadratiske vilkår i x og i og, så vel som lineære termer i begge variablene pluss et uavhengig begrep. Den første symmetriaksen er parallell med den vertikale aksen, og den av den andre er den horisontale aksen.

Generelt sett den kvadratiske ligningen som mangler den kryssede begrepet Xy Det er skrevet som:

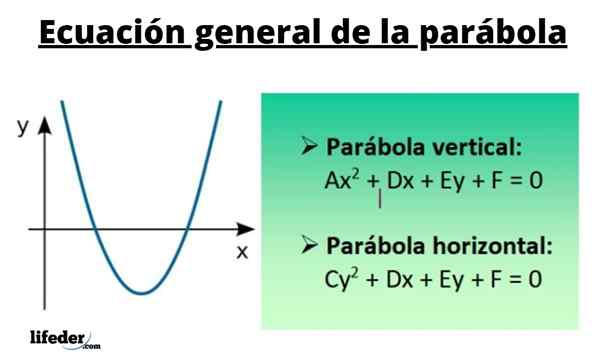
Øks² + Cy² +Dx + ey + f = 0

Verdiene av A, C, D, E og F er reelle tall. Å pålegge betingelsene ved ∙ C = 0 og A+C ≠ 0, kurven som følger av å tegne punktene som tilfredsstiller denne ligningen er en parabola.

Sak 1

For en vertikal lignelse er dens generelle ligning:

Øks² + Dx + ey + f = 0

Hvor a og e er forskjellig fra 0. Med andre ord, når et begrep vises med x², Lignelsen er vertikal.

Sak 2

For sin del, for den horisontale lignelsen har du:

Cy² + Dx + ey + f = 0

Her er C og D også forskjellig fra 0, derfor tilsvarer den kvadratiske uttrykket og².

I alle fall er den generelle ligningen for lignelsen kvadratisk i en av variablene og lineær i den andre.

Lignelseselementer

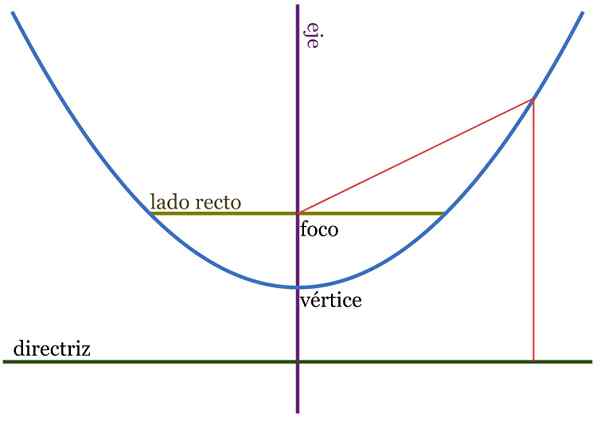Figur 2. Lignelseselementer. Avstandene QF og QH er like. Kilde: Wikimedia Commons.

Parabolaen, definert som et geometrisk sted, består av settet med punkter i ett plan som tilsvarer et annet punkt som heter fokus Og også av en linje, kjent som Rett retningslinje.

Fra den generelle ligningen er det mulig å studere lignelsen ved å spesifisere elementene. Inkludert fokus og retningslinje, er disse elementene beskrevet kort:

-Akser, som refererer til symmetriaksen til parabola, kan være horisontalt (parallelt med abscissa -aksen) eller vertikal (parallelt med ordinatene) aksen).

Kan tjene deg: Vanlig faktor for gruppering av begreper: eksempler, øvelser

-Orientering, som igjen tilsvarer aksenes orientering. Lignelsen er vertikal hvis symmetriaksen er vertikal, og den er horisontalt når aksen også er.

-Toppunkt, Det er punktet der aksen krysser lignelsen.

-Fokus, punkt som ligger på aksen, inne i lignelsen og på avstand p av toppunktet. Alle punktene i parabola ekvist fokus og retningslinjen.

-Parameter, Det er avstanden p Mellom fokuset og toppunktet.

-Rett retningslinje, som er vinkelrett på y -aksen og også en avstand p av toppunktet til lignelsen, men krysser den ikke, siden den er på utsiden.

-Rett side, Det er tauet som går gjennom fokuset, og krysser lignelsen i to punkter, vinkelrett på aksen.

-Eksentrisitet, at i tilfelle av parabolaen er det alltid verdt 1.

-Grafisk representasjon.

Informasjon for å bestemme alle disse elementene er inneholdt i den generelle ligningen.

Den kanoniske formen

For å bestemme elementene i parabolen, er det noen ganger praktisk å gi den generelle formen til den kanoniske formen til den samme, ved hjelp av metoden for å fullføre firkanter i den kvadratiske variabelen.

Denne kanoniske formen er:

(X-H)² = 4p (y-k)

Hvor punkt (h, k) er toppunktet v av lignelsen. Den kanoniske formen til den generelle ligningen kan også bli, utvikle det bemerkelsesverdige produktet og omorganisere vilkårene.

Eksempler

Eksempel 1

Følgende er parabola -ligninger generelt:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -og² = 0

I a) Koeffisientene identifiseres: a = 4, c = 0, d = 0, e = 5, f = -3. Det er en lignelse hvis symmetriakse er vertikal.

Kan tjene deg: syntetisk divisjon

For sin del, i B) gjenstår den generelle ligningen:

- og² + 3x - 2y + 1 = 0

Og koeffisientene er: c = -1, d = 3, e = -2 og f = 1.

Eksempel 2

Neste lignelse er i en kanonisk form:

(Y-1)² = 6 (x-3)

For å finne dens generelle ligning utvikles det bemerkelsesverdige produktet og parentesen utføres til høyre:

og² -2y + 1 = 6x -18

Nå blir alle vilkårene til venstre vedtatt, og de er gruppert praktisk:

og² -2y + 1- 6x +18 = 0 → og² - 6x -2y + 19 = 0

Som det kvadratiske uttrykket er og² Det er en horisontal lignelse. Koeffisientene er:

C = 1; D = -6; E = -2, F = 19.

Løste øvelser

Oppgave 1

Neste lignelse er gitt generelt:

x² -10x -12y - 11 = 0

Det blir bedt om å skrive det i den kanoniske formen.

Løsning

Gå til den kanoniske formen oppnås ved å fullføre firkanter, i dette tilfellet i variabel x. Begrepene i x begynner i parenteser:

(x² -10x) -12y - 11 = 0

Du må forvandle det som er i parenteser til en perfekt firkantet trinomial, som oppnås ved å legge til 5², som naturlig må trekkes fra, for ellers endres uttrykket. Det forblir slik:

(x² −10x+5²) −12y - 11−5²= 0

De tre begrepene i parenteser utgjør den perfekte firkantede trinomialen (X-5)². Det kan sjekkes ved å utvikle dette bemerkelsesverdige produktet for å bekrefte. Nå gjenstår lignelsen:

(X-5)² -12y -36 = 0

Det som følger er å faktorere begrepene utenfor parentesen:

(X-5)² -12 (y +3) = 0

Som endelig forvandles til:

(X-5)² = 12 (y +3)

Eksempel 2

Finn elementene i forrige lignelse og bygg grafikken din.

Løsning

Toppunkt

Parteksen til parabolaen har koordinater V (5, -3)

Det kan tjene deg: hepagonal prisme

Akser

Linjen x = 5.

Parameter

Angående parameterverdien p som vises i den kanoniske formen: (x-h)² = 4p (y-k) sammenligner begge ligningene:

4p = 12

P = 12/4 = 3

Orientering

Denne lignelsen er vertikal og åpnes. Ettersom toppunktet er lokalisert ved x = 5, y = -3, er symmetriaksen den vertikale linjen x = 5.

Fokus

Fokuset er på linjen x = 5, derfor har det en koordinat x = 5 også.

Koordinaten og av fokuset må være p-enheter over k, det vil si: p + k = 3 + (-3) = 0, så er fokuset på punktet (5.0).

Rett retningslinje

Den er vinkelrett på aksen, derfor er den av formen y = c, nå, som en avstand p fra toppunktet er langt fra, men utenfor lignelsen betyr det at det er i en avstand p under k:

y = k -p = -3-3 = -6

Rett side

Dette segmentet kutter til lignelsen, passerer gjennom fokuset og er parallelt med retningslinjen, derfor er det inneholdt i linjen Y = 0.

Grafisk representasjon

Det kan enkelt fås fra gratis online grafikkprogramvare, for eksempel Geogebra. I inngangsboksen er den plassert som følger:

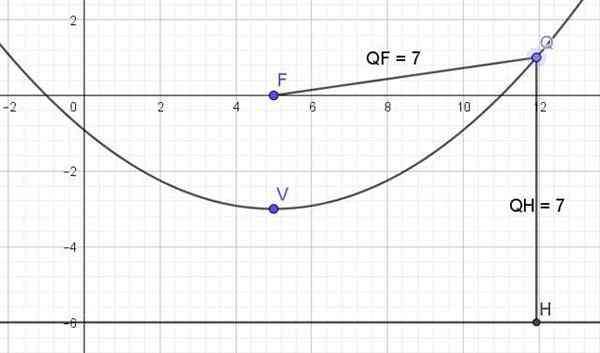Figur 3. Graf over lignelsen x² -10x -12y - 11 = 0. Kilde: f. Zapata.

Referanser

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
2. Hoffman, J. Valg av matematikkproblemer. Volum 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.