Konveks speil

Hva er et konveks speil?

Han Konveks speil Eller divergent er et buet speil, nesten alltid sfærisk og med den reflekterende overflaten på utsiden av sfæren, for eksempel ornamentene i juletreet. Takket være konvekse speil er det mulig.

For eksempel er speilene som er plassert i gatene for å lette transitt av kjøretøyene i smale kors konveks, siden de produserer et bilde med et bredt synsfelt.

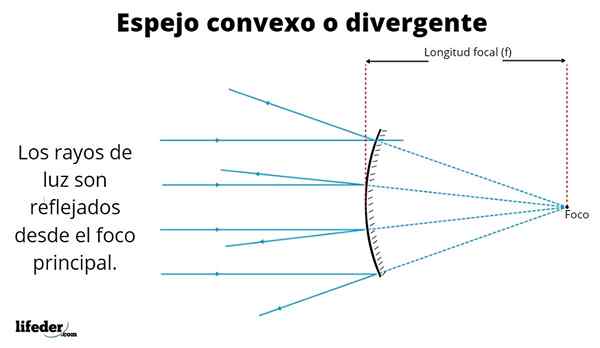
Illustrasjon av et konveks speil

Bildene som er dannet er forskjellige, avhengig av stedet der objektet er plassert. Det overlegne bildet viser parallelle stråler fra en fjern fontene som solen.

Strålene gjenspeiles i henhold til refleksjonsloven, noe som indikerer at lynets vinkel er den samme som den gjenspeiles. Som vi kan se, er de reflekterte strålene atskilt - de krysser ikke - når de forlater den spekulære overflaten, og det er derfor denne typen speil også er kjent som avvikende.

Når refleksjonene strekker seg tilbake fra speilet - diskontinuerlige linjer i figuren - krysser disse på et punkt som kalles fokus.

Kjennetegn på konvekse speil

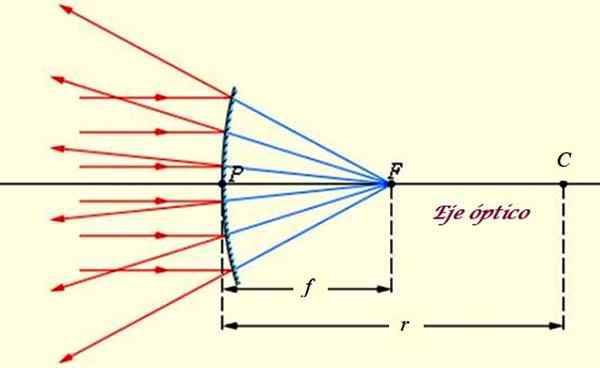Konveks eller divergerende speil, som strålene fra en fjern fontene som solen påvirker. Kilde: f. Zapata.

Det konvekse speilet har følgende egenskaper (se overlegen bilde):

-Speilets bemerkelsesverdige punkter er:

• C Senteret, som faller sammen med sentrum av sfæren som speilet tilhører.
• F fokuset, der strålene reflekterte bak speilet konvergerer.
• Toppunktet P av det samme, som tilsvarer sentrum av den sfæriske overflaten og er kollineal med C og F.

Kan tjene deg: ío (satellitt)

-Har Optisk akse enten Hovedaksen, som er linjen vinkelrett på den spekulære overflaten. Rays som påvirker den optiske aksen gjenspeiles i samme retning.

-Sentrum av sfæren som speilet tilhører er på punkt C og R er dets radius. A C er kjent som Curvature Center, samtidig som r er han Kurvaturradius og indikerer hvor buet speilet er: en mindreårig r, mer fremhevet er den konvekse formen.

-Krysspunktet for de reflekterte strålene er kjent som Brennpunkt av speilet. Avstanden mellom F og P er omtrent r/2:

F = r/2

Dette uttrykket er gyldig for speil hvis størrelse er mye lavere enn krumningsradius.

-Bildet som dannes er mindre og også virtuelt, siden det ligger bak speilet, som vi vil se neste.

Bildedannelse i det konvekse speilet

Å vite hvordan bildet som dannes i det konvekse speilet er strålebehandlingen, som består av å representere lysstrålene som kommer ut av objektet gjennom rette linjer.

Disse strålene reflekteres på overflaten av speilet, og de reflekterte strålene trekkes også. Strålemetoden gjelder for alle slags speil, ikke bare konvekser.

Ved å forlenge de reflekterte strålene, krysser de seg på et bestemt punkt, og det er nettopp der bildet dannes. Utvidelsen av de reflekterte strålene som kommer fra et utvidet objekt som et tre, vises i den nedre figuren med diskontinuerlige linjer.

I de nedre figurene er tre stråler fra objektet tegnet, veldig spesiell og lett å trekke, så vel som refleksjonene:

Kan tjene deg: termisk utvidelse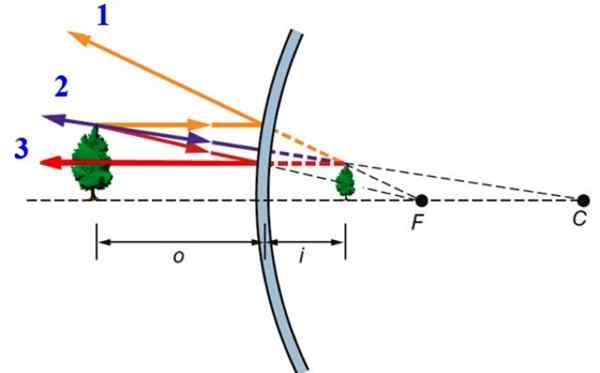 Figur 2.- Bildedannelse i det konvekse speilet. Kilde: f. Zapata.

-Ray 1, som påvirker parallell med den optiske aksen.

-Ray 2, som påvirker eksolitering av den reflekterte strålen passerer nøyaktig gjennom speilets fokus, det vil si punkt F. Denne strålen gjenspeiles parallelt med den optiske aksen.

-Endelig Ray 3, som når vinkelrett på den sfæriske overflaten, og av denne grunn gjenspeiles det i samme retning.

I prinsippet gjelder denne prosedyren for hvert punkt i treet, men med informasjonen hentet fra de 3 trukket strålene er det nok å finne bildet av objektet: det dannes bak speilet, den er riktig og mindre enn originalen.

Eksempler og anvendelser av konvekse speil

Mange veldig trukket sfæriske overflater fungerer som konvekse speil, for eksempel lyse og sølv julepynt, så vel som nye og lyse stålbiler.

Også konvekse speil har mange praktiske anvendelser, for eksempel:

Speil for å forhindre trafikkulykker

Konvekse speil i gater og veier er med på å unngå ulykker, siden de lar deg se trafikken som kommer fra hjørnene.

Overvåkningsspeil

I butikker og banker er det vanligvis konvekse speil for å oppdage tyver, samt for å unngå kollisjoner mellom mennesker og gaffeltruckbiler som sirkulerer i hallene og mellom hyllene.

Bakspeil

Biler og motorsykler har konvekse speil, som produserer litt mindre bilder, men dekker mer synsfelt enn flate speil.

Cassegrain teleskop

Et av speilene i Cassegrain -reflektoren, sekundærspeilet, er konveks, selv om det ikke er sfærisk og tjener til å gjenspeile bildet mot hovedspeilet i teleskopet.

Kan tjene deg: Gravitasjonsenergi: Formler, egenskaper, applikasjoner, øvelser

Konvekse speilligninger

Tenk på rektanglene til følgende figur, bestemt av Ray 1, som kommer fra toppen av pilen, dens refleksjon og utvidelsen av dette.

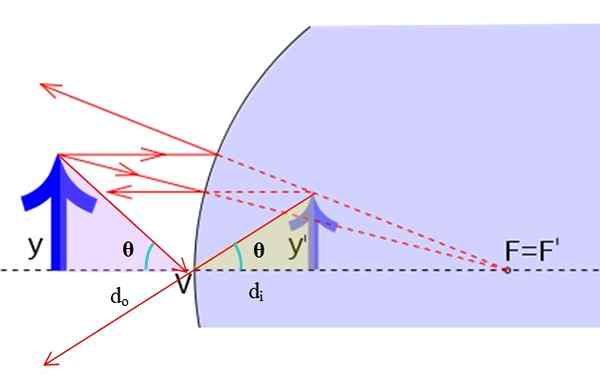Geometri for å finne speilforstørrelsen. Kilde: f. Zapata.

Det opprinnelige bildet har høyde, og mens høyden på det virtuelle bildet er og ' . Det er sant, det:

Tan θ = y/d_enten = Y '/d_Yo

Speilforstørrelse

Årsaken mellom høyden på bildet og høyden på objektet er speilforstørrelse, Det kalles det, selv om det oppnådde bildet er mindre enn det virkelige objektet. Vi betegner det av m:

M = y '/ y = d_Yo /d_enten

Forholdet mellom objektet og dets bilde i det konvekse speilet

La oss nå vurdere denne andre figuren, der AVF -regionen kan betraktes som en riktig trekant, siden speilets krumning ikke er veldig uttalt. Derfor:

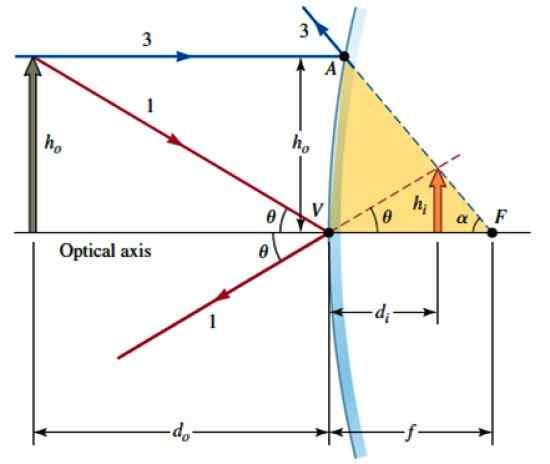Geometri for å finne det matematiske forholdet mellom objektet og dets bilde. Kilde: Katz, D. Fysikk for forskere og ingeniører.

Av ≈ h_enten

Så:

Tan α = h

Derfor:

Det inverse av dette uttrykket er forstørrelsen, da:

Derfor:

1- (d_Yo /f) = D_Yo /d_enten

Ved å dele alt mellom D_Yo:

Endelig:

 Nå, for speil, gjelder noen tegnkonvensjoner. Selv om vi vet at en avstand alltid er positiv, skilles de i alle avstander bak speilet med et negativt tegn.

Derfor, som F og d_Yo De er bak speilet, de blir lagt et skilt mindre, mens for avstanden d_enten Det er ikke nødvendig, siden det er foran speilet. Dermed gjenstår den forrige ligningen:

Det kan demonstreres at denne ligningen også er gyldig for det konkave speilet.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 2. Mc Graw Hill.
2. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
3. Katz, d. 2017. Fysikk for forskere og ingeniører. Cengage Learning.
4. Thomas, w. 2008. Konseptuell fysikk. McGraw Hill.
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.