Matte

Overjektive funksjon, egenskaper, eksempler

Overjektive funksjon, egenskaper, eksempler

EN OVERIVISJON FUNKSJON Det er ethvert forhold der hvert element som tilhører Codominium er et bilde av minst ett domeneelement. Også kjent som funksjon Om, De er en del av klassifiseringen av funksjoner angående måten elementene deres er relatert til.

For eksempel en funksjon F: a → B definert av F (x) = 2x

Som leses "F det går fra TIL før B definert av F (x) = 2x "

Berøring Definer start- og ankomstsett A og b.

A: 1, 2, 3, 4, 5 Nå verdiene eller bildene som hvert av disse elementene vil bli utgitt når de blir evaluert i F, De vil være elementene i codominium.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Dermed danner settet B: 2, 4, 6, 8, 10

Det kan konkluderes da at:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 definert av F (x) = 2x er en oversvivende funksjon

Hvert element i kodominiet må være minst en operasjon av den uavhengige variabelen gjennom den aktuelle funksjonen. Det er ingen bildegrensende, et element av codominium kan være et bilde av mer enn ett element i domenet og fortsette å håndtere en OVERIVISJON FUNKSJON.

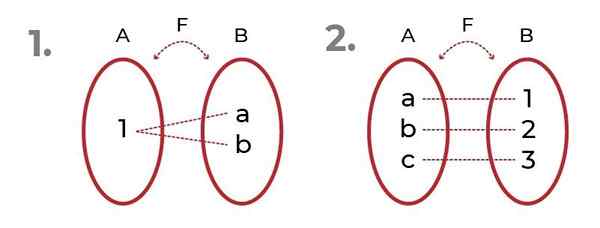
Bildet viser 2 eksempler med Onjektive funksjoner.

Kilde: Forfatter

I det første observeres det at bildene kan henvises til det samme elementet, uten at det går ut over Overvisning av funksjonen.

I det andre ser vi en rettferdig fordeling mellom domene og bilder. Dette gir opphav til Bijektivfunksjon, hvor kriteriene for Injeksjonsfunksjon og oversvektiv funksjon.

En annen metode for å identifisere Onjektive funksjoner, er å bekrefte om kodominiet er lik funksjonens rangering. Dette betyr at hvis ankomstsettet er lik bildene som leveres av funksjonen når du evaluerer den uavhengige variabelen, Funksjonen er oversvivende.

[TOC]

Egenskaper

Å overveie Overvirkende Følgende må oppfylles til en funksjon:

Være F: dF → CF

∀ B ℮ CF  OG til ℮  DF   / F (a) = b

Dette er den algebraiske måten å etablere det på For alle "B" som tilhører CF Det er en "A" som tilhører DF  slik at F -funksjonen evaluert i "A" er lik "B". 

Det kan tjene deg: radikale egenskaper

Overvisning er en særegenhet ved funksjoner, der codominium og rang er like. Dermed utgjør elementene evaluert i funksjonen ankomstsettet.

Kondisjonering av funksjoner

Noen ganger en funksjon som ikke er Overvirkende, kan gjennomgå en viss kondisjonering. Disse nye forholdene kan gjøre det til en OVERIVISJON FUNKSJON.

Alle typer modifikasjoner av funksjonen og kodominiet til funksjonen er gyldige, der målet er å oppfylle overvisningsegenskapene i det tilsvarende forholdet.

Eksempler: Løste øvelser

Å møte forholdene til Overvisning Ulike kondisjoneringsteknikker bør brukes, dette for å sikre at hvert element i kodominiet er innenfor settet med bilder av funksjonen.

Oppgave 1

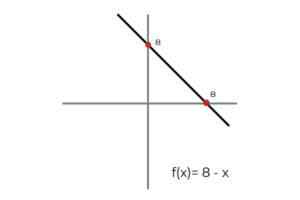
  • Være funksjonen F: r → R definert av linjen F (x) = 8 - x

A: [Alle reelle tall]

Kilde: Forfatter

I dette tilfellet beskriver funksjonen en kontinuerlig linje, som dekker alle reelle tall både i deres domene og rekkevidde. Fordi funksjonens rangering RF Det er lik kodominium R Det kan konkluderes med at:

F: r → R definert av linjen F (x) = 8 - x er en OVERIVISJON FUNKSJON.

Dette gjelder alle lineære funksjoner (funksjoner hvis større grad av variabelen er en).

Oppgave 2

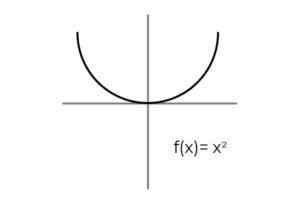
  • Studere funksjonen F: r → R definert av F (x) = x2 : Definere om det er en OVERIVISJON FUNKSJON. I tilfelle det ikke er det, vis den nødvendige kondisjonen for å gjøre det overvektivt.
Kilde: Forfatter

Den første tingen å vurdere er kodominiet til F, som består av reelle tall R. Det er ingen måte for funksjonen å kaste negativ verdi, noe som utelukker negative ekte blant mulige bilder.

Kondisjonering av intervallet codominium [0 , ∞ ]. Det unngås å forlate elementer i co -alomio uten å relatere gjennom F.

Bildene gjentas for par elementer i den uavhengige variabelen, for eksempel x = 1 og x = - 1.  Men dette påvirker bare Injektivitet  av funksjonen, ikke å være et problem for denne studien.

Kan tjene deg: påfølgende derivater

På denne måten kan det konkluderes med at:

F: r  →[0, ∞ ) definert av F (x) = x2    Det er en oversvivende funksjon

Øvelse 3

  • Definere forholdene til kodominiet de ville Overvirkende til funksjoner

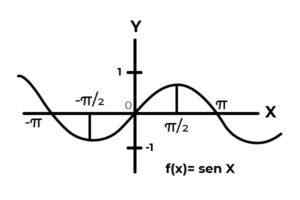
F: r  → R definert av F (x) = sin (x)

F: r  → R definert av F (x) = cos (x)

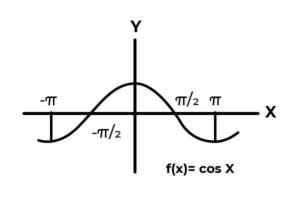Kilde: Forfatter Kilde: Forfatter.

Oppførselen til trigonometriske funksjoner ligner på bølger, og er veldig vanlig å finne repetisjoner av den avhengige variabelen mellom bildene. Også i de fleste tilfeller er funksjonen for funksjonen begrenset til en eller flere sektorer av den virkelige linjen.

Dette er tilfelle av sinus og kosinusfunksjoner. Der verdiene deres svinger i intervallet [-1, 1]. Nevnte intervall må kondisjonere codominium for å oppnå konvolutten til funksjonen.

F: r  →[-eleven] definert av F (x) = sin (x)  Det er en oversvivende funksjon

F: r  →[-eleven]definert av F (x) = cos (x) Det er en oversvivende funksjon

Oppgave 4

  • Studere funksjonen

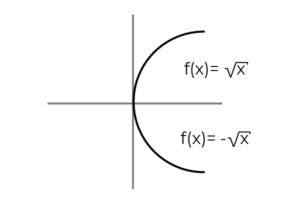
F: [0, ∞ ) → R definert av F (x) = ± √x   betegner hvis det er en OVERIVISJON FUNKSJON

Kilde: Forfatter

Funksjonen F (x) = ± √x  Det har den spesielle som definerer 2 avhengige variabler ved hver verdi av "x" . Det vil si at området mottar 2 elementer for hvert som utføres i domenet. En positiv og negativ verdi for hver verdi av "x" må verifiseres for hver verdi av "x".

Når du observerer startmonteringen, bemerkes det at domenet allerede er begrenset, dette for å unngå ubestemmelser som produseres når du evaluerer et negativt tall i en dreiemomentrot.

Når du verifiserer funksjonsområdet, viser det at hver codominium -verdi tilhører området.

På denne måten kan det konkluderes med at:

F: [0, ∞ ) → R definert av F (x) = ± √x  Det er en oversvivende funksjon

Kan tjene deg: Samtidig vektorer: Kjennetegn, eksempler og øvelser

Oppgave 4

  • Studere funksjonen F (x) = ln x  betegner hvis det er en OVERIVISJON FUNKSJON. Tilstand ankomst og avgangssett for å tilpasse funksjonen til kriteriene for overvisning.
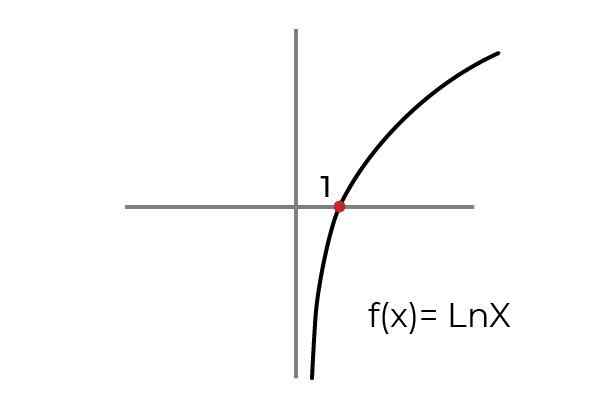Kilde: Forfatter

Som vist i grafen funksjonen F (x) = ln xer definert for verdiene til "x" større enn null. Mens verdiene til "og" eller bilder kan ta noen reell verdi.

På denne måten kan vi begrense domenet til F (x) = til intervallet (0 , ∞ )

Mens funksjonens rangering kan opprettholdes som sett med reelle tall R.

Med tanke på dette kan det konkluderes med at:

F: [0, ∞ ) → R definert av F (x) = ln x  Det er en oversvivende funksjon

Oppgave 5

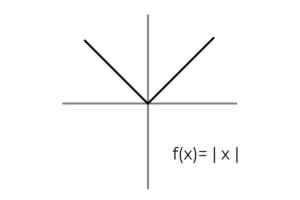
  • Studer absolutt verdifunksjon F (x) = | x | og utpeke ankomst- og avgangssettene som er samlet til kriteriene for allegivitet.
Kilde: Forfatter

Funksjonens domene er oppfylt for alle reelle tall R. På denne måten må den eneste kondisjonen utføres i kodominiet, med hensyn til at den absolutte verdifunksjonen bare tar positive verdier.

Kodominiet til funksjonen er etablert utjevning av den til området for det samme

[0 , ∞ )

Nå kan det konkluderes med at:

F: [0, ∞ ) → R definert av F (x) = | x |  Det er en oversvivende funksjon

Foreslåtte øvelser

  1. Kontroller om følgende funksjoner er overvektive:
  • F: (0, ∞ ) → R definert av F (x) = log (x + 1)
  • F: r → R definert av F (x) = x3
  • F: r →[1, ∞ )  definert av F (x) = x2  + 1
  • [0, ∞ ) → R definert av F (x) = log (2x + 3)
  • F: r → R definert av F (x) = sek x
  • F: r - 0 → R definert av F (x) = 1 / x

Referanser

  1. Introduksjon til logikk og kritisk tenking. Merrilee h. Laks. University of Pittsburgh
  2. Problemer i matematisk analyse. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Stang.
  3. Elementer av abstrakt analyse. Mícheál O'Searcoid PhD. Institutt for matematikk. University College Dublin, Beldfield, Dublind 4
  4.  Introduksjon til logikk og til metodikken til de deduktive vitenskapene. Alfred Tarski, New York Oxford. Oxford University Press.
  5.  Matematiske analyseprinsipper. Enrique Linés Escardó. Redaksjonell tilbakevending. Til 1991. Barcelona, ​​Spania.