Trigonometriske begrenser hvordan du løser dem, løste øvelser

De trigonometriske grenser De er grenser for funksjoner slik at disse funksjonene er dannet av trigonometriske funksjoner.

Det er to definisjoner som må være kjent for å forstå hvordan beregningen av en trigonometrisk grense blir utført. Disse definisjonene er:

- Grense for en "f" -funksjon når "x" har en tendens til "b": den består av å beregne verdien som f (x) nærmer seg når "x" nærmer seg "b", uten å hevde "b".

- Trigonometriske funksjoner: trigonometriske funksjoner er henholdsvis sine kosinus- og tangentefunksjoner, betegnet med sin (x), cos (x) og solbrun (x).

De andre trigonometriske funksjonene oppnås fra de tre funksjonene nevnt ovenfor.

Funksjoner grenser

For å avklare konseptet med en funksjonsgrense, vil vi fortsette å vise noen eksempler med enkle funksjoner.

- Grensen for f (x) = 3 når "x" har en tendens til "8" er lik "3", siden funksjonen alltid er konstant. Det spiller ingen rolle hvor mye "x" er verdt, verdien av f (x) vil alltid være "3".

- Grensen for f (x) = x-2 når "x" har en tendens til "6" er "4". Siden når "X" er nær "6", nærmer "X-2" seg "6-2 = 4".

- Grensen for g (x) = x² når "x" har en tendens til "3" er lik 9, siden "X" nærmer seg "3" 3 ", nærmer seg" 3² = 9 ".

Som det kan bemerkes i de foregående eksemplene, består beregning av en grense i å evaluere verdien som "x" har en tendens til i funksjonen, og resultatet vil være verdien av grensen, selv om dette bare gjelder for kontinuerlige funksjoner.

Er det mer kompliserte grenser?

Svaret er ja. De foregående eksemplene er de enkleste eksemplene på grenser. I beregningsbøker er hovedgrenseøvelsene de som genererer en ubestemmelse av type 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 og (∞)^0.

Kan tjene deg: Pythagorean identiteter: Demonstrasjon, eksempel, øvelser

Disse uttrykkene kalles ubestemmelser siden de er uttrykk som matematisk gir mening.

I tillegg til det, avhengig av funksjonene som er involvert i den opprinnelige grensen, kan resultatet oppnådd når du løser ubestemmelsene være forskjellige i hvert tilfelle.

Eksempler på enkle trigonometriske grenser

For å løse grenser er det alltid veldig nyttig å kjenne grafene til de involverte funksjonene. Nedenfor er grafene til bihule-, kosinus- og tangensfunksjonene.

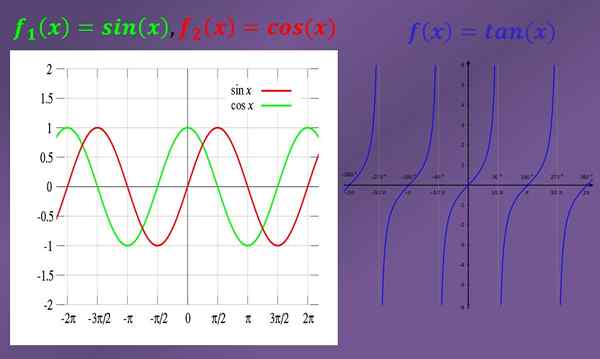
Noen eksempler på enkle trigonometriske grenser er:

- Beregn uten (x) grensen når "x" har en tendens til "0".

Når du ser grafen, kan du se at hvis "x" nærmer seg "0" (både til venstre og høyre), så nærmer grafikken til brystet seg også "0". Derfor er syndsgrensen (x) når "x" har en tendens til "0" er "0".

- Beregn grensen til cos (x) når "x" har en tendens til "0".

Når man observerer grafen til kosinuset, kan det sees at når "x" er nær "0", så er grafen til kosinuset nær "1". Dette innebærer at grensen til cos (x) når "x" har en tendens til "0" er lik "1".

En grense kan eksistere (å være et tall), som tilfellet er i de tidligere eksemplene, men det kan også hende at det ikke eksisterer som vist i følgende eksempel.

- Grensen for solbrun (x) når "x" har en tendens til "π/2" til venstre er lik "+∞", som det kan sees i grafikken. På den annen side er grensen for solbrun (x) når "x" har en tendens til "-π/2" til høyre er lik "-∞".

Trigonometriske begrenser identiteter

To veldig nyttige identiteter når trigonometriske grenser blir beregnet er:

Kan tjene deg: Ikke -lineær programmering: Metoder og øvelser

- Grensen for "sin (x)/x" når "x" har en tendens til "0" er lik "1".

- Grensen for "(1-kos (x))/x" når "x" har en tendens til "0" er lik "0".

Disse identitetene brukes veldig ofte når du har en slags ubestemmelse.

Løste øvelser

Løs følgende grenser ved å bruke identitetene beskrevet ovenfor.

- Oppgave 1

Beregn grensen for "f (x) = uten (3x)/x" når "x" har en tendens til "0".

Hvis "F" -funksjonen blir evaluert i "0", vil en ubestemmelse av type 0/0 oppnås. Derfor må vi prøve å løse denne ubestemmelsen ved å bruke de beskrevne identitetene.

Den eneste forskjellen mellom denne grensen og identiteten er tallet 3 som vises innenfor sinusfunksjonen. For å anvende identiteten, må "f (x)" -funksjonen skrives om som følger "3*(uten (3x)/3x)". Nå er både brystargumentet og nevneren like.

Så når "x" har en tendens til "0", er bruk av identitet "3*1 = 3". Derfor er grensen for f (x) når "x" har en tendens til "0" lik "3".

- Oppgave 2

Beregn grensen for “g (x) = 1/x - cos (x)/x” når “x” har en tendens til “0”.

Når “x = 0” erstattes i g (x) en ubestemmelse av typen ∞ -∞. For å løse det blir brøkene trukket fra, noe som gir som et resultat "(1-kos (x))/x".

Nå, ved å bruke den andre trigonometriske identiteten, er grensen for g (x) at "x" har en tendens til "0" er lik 0.

- Øvelse 3

Beregn grensen for "H (x) = 4Tan (5x)/5x" når "X" har en tendens til "0".

Igjen hvis H (x) blir evaluert i “0”, vil en ubestemmelse av type 0/0 oppnås.

Omskriving som (5x) som uten (5x)/cos (5x) viser det seg at h (x) = (uten (5x)/5x)*(4/cos (x)))).

Det kan tjene deg: Innskrevet vinkel på en sirkel: Definisjon, teoremer, eksempler

Bruke at grensen på 4/cos (x) når “x” har en tendens til “0” er lik “4/1 = 4” og den første trigonometriske identiteten oppnås at grensen på H (x) når “x” har en tendens "0" er lik "1*4 = 4".

Observasjon

Trigonometriske grenser er ikke alltid lett å løse. I denne artikkelen ble det bare vist grunnleggende eksempler.

Referanser

1. Fleming, w., & Varberg, D. OG. (1989). Prealculus matematikk. Prentice Hall Ptr.
2. Fleming, w., & Varberg, D. OG. (1989). Precalculus matematikk: en problemløsende tilnærming (2, illustrert Ed.). Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Algebra og trigonometri med analytisk geometri. Pearson Education.
4. Larson, r. (2010). Prealculus (8 utg.). Cengage Learning.
5. Lojal, j. M., & Viloria, n. G. (2005). Flat analytisk geometri. Mérida - Venezuela: Venezuelansk redaksjon C. TIL.
6. Pérez, ca. D. (2006). Prequalculus. Pearson Education.
7. Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning (Niende utg.). Prentice Hall.
8. Saenz, J. (2005). Differensialberegning med tidlige transcendente funksjoner for vitenskap og ingeniørfag (Second Edition Ed.). Hypotenuse.
9. Scott, c. TIL. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (Reprint Ed.). Lynkilde.
10. Sullivan, m. (1997). Prequalculus. Pearson Education.