Jevn akselererte rettlinjede bevegelsesegenskaper, formler

Han jevn akselerert rettlinjet bevegelse Det er den som passerer over en rett linje og hvor mobilen øker eller reduserer hastigheten med konstant hastighet. Denne hastigheten er størrelsen som beskriver rytmen som hastigheten endres og kalles akselerasjon.

Når det. I andre typer bevegelse er akselerasjon også i stand til å endre retning og hastighetsfølelse, eller til og med endre retningen, som i den ensartede sirkulære bevegelsen.

Figur 1. Akselererte bevegelser er de hyppigste. Kilde: Pixabay.

Siden akselerasjonen representerer endringen av hastighet over tid, er enhetene i det internasjonale systemet M/S² (meter på sekunder kvadrat). Som hastighet kan akselerasjon tildeles positivt eller negativt tegn, ettersom hastigheten øker eller avtar.

En akselerasjon sier på +3 m/s² Det betyr at for hvert sekund som går øker mobilhastigheten med 3 m/s. Hvis den i begynnelsen av bevegelsen (ved t = 0) var mobilhastigheten +1 m/s, vil den etter et sekund være 4 m/s og etter 2 sekunder vil den være 7 m/s.

I den enhetlige varierte rettlinjede bevegelsen blir hastighetsvariasjonene som mobile objekter daglig opplevelse tatt i betraktning i betraktning. Det er en mer realistisk modell enn den ensartede rettlinjede bevegelsen. Fortsatt er det fremdeles ganske begrenset, da det begrenser mobilen til å reise bare på en rett linje.

[TOC]

Kjennetegn

Dette er hovedegenskapene til den jevnt akselererte rettlinjede bevegelsen:

-Bevegelsen passerer alltid langs en rett linje.

-Akselerasjonen av mobilen er konstant, både i størrelse og i retning og betydning.

-Mobilhastighet øker (eller reduserer) lineær.

-Siden akselerasjon til forblir konstant over tid t, Grafen med størrelsesorden som en funksjon av tid er en rett linje. I eksemplet vist i figur 2 er linjen blå og akselerasjonsverdien leses på den vertikale aksen, omtrent +0.68 m/s².

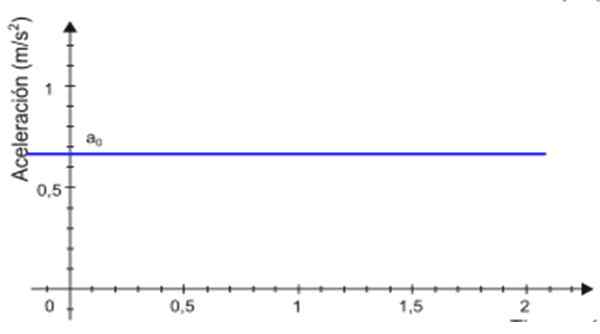Figur 2. Akselerasjonsgraf i henhold til tid for en jevn variert rettlinjet bevegelse. Kilde: Wikimedia Commons.

-Hastighetskartet v Om t Det er en rett linje (i grønt i figur 3), hvis skråning tilsvarer mobil akselerasjon. I eksemplet er skråningen positiv.

Det kan tjene deg: Bornitrid (BN): Struktur, egenskaper, innhenting, bruk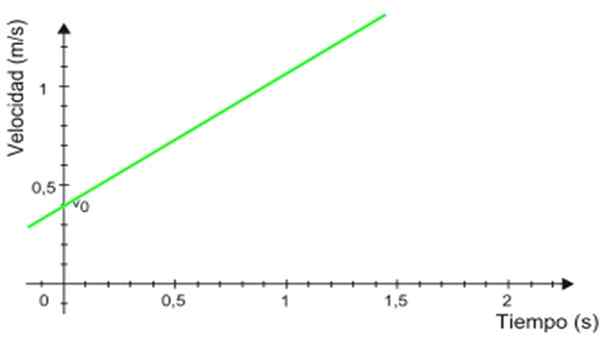 Figur 3. Hastighetsgraf basert på tid for en jevn variert rettlinjet bevegelse. Kilde: Wikimedia Commons.

-Kuttet med den vertikale aksen indikerer den opprinnelige hastigheten, i dette tilfellet er det 0.4 m/s.

-Endelig er grafen til X -posisjonen kontra tid kurven vist i rødt i figur 4, som alltid er en lignelse.

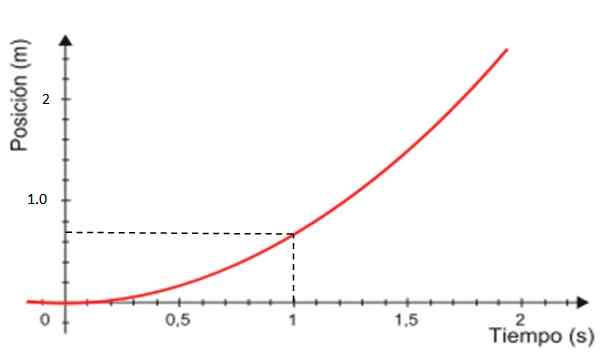Figur 4. Grafikk av stillingen basert på tid for en jevn variert rettlinjet bevegelse. Kilde: Modified Wikimedia Commons.

Avstand reist fra graf V vs. t

Ved å ha graf V vs. t, beregningen av avstanden som er reist av mobilen er veldig enkel. Den tilbakelagte avstanden tilsvarer området under linjen som er inkludert i ønsket tidsintervall.

I eksemplet som vises, antar du at du vil vite avstanden som er reist av mobilen mellom 0 og 1 sekund. Ved å bruke denne grafen, se figur 5.

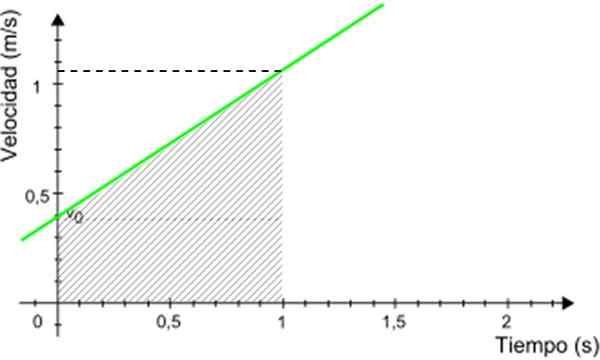Figur 5. Graf for å beregne avstanden som er reist av mobilen. Kilde: Modified Wikimedia Commons.

Avstanden som ble søkt numerisk ekvivalent med området med skyggelagt trapesoid i figur 3. Trapezoidområdet er gitt av: (Hovedbase + mindre base) x høyde/2

Avstand reist = (0.4 + 1.05) x 1/2 m = 0.725 m

Det er også mulig å dele det skyggelagte området i en trekant og et rektangel, beregne de tilsvarende områdene og legge dem til. Avstanden er positiv, selv om partikkelen går til høyre eller til venstre.

Formler og ligninger

Både gjennomsnittlig akselerasjon og øyeblikkelig akselerasjon har samme verdi i MRUV, derfor:

-Akselerasjon: til = konstant

Når akselerasjonen er lik 0, er bevegelsen ensartet rettlinjig, siden hastigheten vil være konstant i dette tilfellet. Tegnet på til Det kan være positivt eller negativt.

Siden akselerasjonen er skråningen på linjen V mot T, er ligning V (t):

-Hastighet avhengig av tid: v (t) = v_enten + PÅ

Hvor v_enten Det er den første mobilhastighetsverdien

-Posisjon avhengig av tid: x (t) = x_enten + v_enten T +½at² 

Når tiden ikke er tilgjengelig, men i stedet er det hastigheter og forskyvninger, er det en veldig nyttig ligning som oppnås ved å fjerne tiden for v (t) = v_enten + PÅ og erstatte den i den siste ligningen. Er om:

Kan tjene deg: Potensiell energi: Kjennetegn, typer, beregning og eksempler

-Ligning som ikke inneholder tid: v² = v_enten² +2.til.Δx

Løste øvelser

Når du løser en kinematikkøvelse, er det viktig å sikre at situasjonen som foreslås tilpasser seg modellen som skal brukes. For eksempel er likningene av den ensartede rettlinjede bevegelsen ikke gyldige for en akselerert bevegelse.

Og de av den akselererte bevegelsen er ikke gyldige for en sirkulær eller krøllete bevegelse, for eksempel. Den første av disse øvelsene løst nedenfor kombinerer to mobiler med forskjellige bevegelser. For å løse det riktig, er det nødvendig å gå til riktig bevegelsesmodell.

-Trening løst 1

For å finne ut dybden på en brønn, slipper et barn en mynt og aktiverer samtidig stoppeklokken, som stopper nettopp når du lytter til valutakuppet mot vann. Lesingen var 2.5 sekunder. Å vite at lydhastigheten i luften er 340 m/s, beregne dybden på brønnen.

Løsning

Være h Dybden på brønnen. Valutaen reiser denne avstanden i fritt fall, en jevn variert vertikal bevegelse, med innledende hastighet 0, siden valutaen er droppet, og konstant akselerasjon ned på den samme som 9.8 m/s². Ta en tid t_m Ved å gjøre dette.

Når valutaen kolliderer med vann, reiser lyden forårsaket av klikket opp til barnets øre, som stopper stoppeklokken når du lytter til den. Det er ingen grunner til å tro at hastigheten på lyden endres mens du klatrer på brønnen, så lydbevegelsen er ensartet rettlinjet. Lyden tar tid t_s For å nå barnet.

Bevegelsesligning for valutaen:

H = ½.g.t_m ² = 4.9 t_m ²

Der de er erstattet x og til av ligningen for posisjonen gitt i forrige seksjon, av h og g.

Lydbevegelsesligning:

h = v_s . t_s = 340 t_s

Dette er den kjente ligningen Avstand = hastighet x tid. Med disse to ligningene er det tre ukjente: H, TM og TS. I tider er det et forhold, er det kjent at alt tar 2.5 sekunder som skjer, derfor:

t_m + t_s = 2.5 s

Utjevning av begge ligningene:

4.9 t_m ² = 340 t_s

Å rydde en av tidene og erstatte:

4.9 t_m ²= 340.(2.5 - t_m)

Når du utvikler begrepet til høyre og transponerer begreper, oppnås det:

Kan tjene deg: Vertikal skudd: Formler, ligninger, eksempler

4.9 t_m ²+340 t_m - 850 = 0

Dette er en andre grads ligning med to løsninger: 2.416 og -71.8. Den positive løsningen er valgt, som er den som gir mening, siden tiden ikke kan være negativ og i alle fall må være mindre enn 2.5 sekunder. For denne tiden oppnås det ved å erstatte dybden på brønnen:

4.9 t_m ²= 4.9 x 2.416² M = 28.6 m

-Trening løst 2

En bil som reiser ved 90 km/t nærmer seg en tverrgående mulighet med trafikklys. Når det er 70 m der, er det gule lyset slått på, hvis varighet er 4 sekunder. Avstanden mellom trafikklyset og neste hjørne er 50 m.

Sjåføren har disse to alternativene: a) stå på - 4 m/s² eller b) akselerere ved + 2 m/s². Hvilke av de to alternativene lar sjåføren stoppe eller krysse hele avenyen før lyset endres til rødt?

Løsning

Driverens startposisjon er x = 0 akkurat når han ser det gule lyset. Det er viktig å konvertere enhetene riktig: 90 km/t tilsvarer 25 m/s.

I henhold til alternativ A), i løpet av de 4 sekundene som det gule lyset varer sjåføren, reiser:

x (t) = v_enten T +½at²= 25.4 -½.(-4).4²M = 68 m (2 meter før trafikklyset)

Analysere alternativ b) Du har:

x (t) = v_enten T +½at²= 25.T +½.2.t²

Mens det gule lyset varer, reiser sjåføren på denne måten:

x = 25.4 +½.2.4²M = 116 m

Men 116 m er mindre enn avstanden som er tilgjengelig for å nå neste hjørne, som er 70 + 50 m = 120 m, derfor klarer den ikke å krysse hele gaten før det røde lyset er slått på. Den anbefalte handlingen er å stoppe og holde seg 2 meter fra trafikklyset.

applikasjoner

Hver dag opplever folk effekten av akselerasjon: når de reiser med bil eller buss, siden de kontinuerlig trenger å stoppe og akselerere for å tilpasse marsjen til hindringene på veien. Akselerasjon oppleves også når den går opp eller ned i en heis.

Morsomme parker er nettsteder der folk betaler for å oppleve effekten av akselerasjon og ha det gøy.

I naturen observeres den jevnt varierte rettlinjede bevegelsen når et objekt slippes fritt, eller når det kastes vertikalt opp og forventes å komme tilbake til bakken. Hvis luftmotstanden blir foraktet, er verdien av akselerasjon av tyngdekraften: 9.8 m/s2.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.40-45.
2. Figueroa, d. Fysisk serie for vitenskap og ingeniørfag. Volum 3. Utgave. Kinematikk. 69-85.
3. Giancoli, d.  Fysikk: Prinsipper med applikasjoner. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fysikk 10. Pearson Education. 116-119