Tachtenberg -metoden hva er, eksempler

Han Trachtenberg -metoden Det er et system å utføre aritmetiske operasjoner, hovedsakelig multiplikasjon, på en enkel og rask måte, når deres regler har blitt kjent og dominert.

Han ble utviklet av den russiske ingeniøren Jakow Trachtenberg (1888-1953) da han var en fange av nazistene i en konsentrasjonsleir, som en form for distraksjon for å opprettholde fornuft mens han fortsatte i fangenskap.

Figur 1. Multiplikasjonstabeller. Kilde: Wikimedia Commons. Taulacat [CC By-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)] [TOC]

Hva er fordeler og ulemper

Fordelen som denne metoden representerer er at for å utføre multiplikasjoner er det ikke nødvendig.

Ulempen er at det ikke er noen universell regel å multiplisere med noe tall, men regelen varierer i henhold til multiplikatoren. Mønstre er imidlertid ikke vanskelig å huske og tillater i prinsippet operasjoner uten papir og blyant.

Gjennom denne artikkelen vil vi konsentrere oss om reglene for raskt å formere seg.

[TOC]

Eksempler

For å bruke metoden er det nødvendig å kjenne reglene, så vi vil presentere dem en etter ett og med eksempler:

- Multipliser et figur med 10 eller 11

Multiplikasjonsregel med 10

-For å multiplisere et hvilket som helst figur med 10, legges en null ganske enkelt til høyre. For eksempel: 52 x 10 = 520.

Regler for å multiplisere med 11

-En null legges til begynnelsen og på slutten av figuren.

-Hvert siffer er lagt til med sin høyre -håndte nabo, og resultatet plasseres under det tilsvarende sifferet til den opprinnelige figuren.

-Hvis resultatet overstiger ni, blir enheten notert og et lite punkt plasseres for å huske at vi har en enhet som vil bli lagt til i summen av neste figur med sin høyre -hånds nabo.

Detaljert multiplikasjonseksempel med 11

Multipliser 673179 med 11

Kan tjene deg: konvergensradio: Definisjon, eksempler og øvelser løst

06731790 x 11 =

--

= 7404969

De nødvendige trinnene for å nå dette resultatet, illustrert gjennom farger, er følgende:

-1 av multiplikatorenheten (11) ble multiplisert med multiplikator 9 (06731790) og den ble lagt til 0. Unity -sifferet ble oppnådd: 9.

-Så multipliserer den 1 med 7 og legger til ni gir 16 og vi har 1, dusin siffer er plassert: 6.

-Deretter multipliser 1 med 1 blir lagt til naboen til høyre 7 pluss 1 som ledet som et resultat 9 For hundre.

-Neste figur oppnås fra å multiplisere 1 med 3 pluss naboland 1, det resulterer 4 For siffer på tusenvis.

-Den multipliseres 1 med 7 og naboen blir lagt til resulterende 10, null er plassert (0) som tiende siffer og det tar en.

-Da 1 for 6 pluss nabo 7 er 13 pluss en 1 som var 14, 4 som et siffer av hundreusen og tar 1.

-Til slutt multipliser 1 med null som ble lagt til begynnelsen, og ga null mer naboen 6 pluss en som tok. Det er endelig 7 For sifferet som tilsvarer millionene.

- Multiplikasjon med tall fra 12 til 19

Å multiplisere med 12 ethvert figur: 

-En null legges til begynnelsen og en annen null på slutten av figuren for å multiplisere.

-Hvert siffer er doblet fra figuren for å bli multiplisert og legger til med sin høyre -håndte nabo.

-Hvis summen overstiger 10, legges en enhet til neste dupliseringsoperasjon og legger til med naboen.

Eksempel på multiplikasjon med 12

Multipliser 63247 med 12

0632470 x 12 =

-

758964

Detaljene for å nå dette resultatet, strengt etter reglene som er angitt, vises i følgende figur:

Figur 2. Trachtenberg -metoden for å multiplisere et hvilket som helst tall med 12. Kilde: f. Zapata.

- Utvidelse av reglene for multiplikasjoner med 13, ... til 19

Multiplikasjonsmetoden med 12 kan utvides til multiplikasjoner med 13, 14 til 19 bare endrer dupliseringsregelen for tilfelle av tretten, firedoblet i tilfelle 14 og så videre til den når 19.

Kan tjene deg: ortogonal matrise: egenskaper, demonstrasjon, eksempler

Regler for produkter innen 6, 7 og 5

- Multiplikasjon med 6

-Legg nuller til begynnelsen og slutten av figuren som skal multipliseres med 6.

-Legg til halvparten av høyre til høyre for hvert siffer, men hvis sifferet er rart å legge til 5 i tillegg.

Figur 3. Multiplikasjon av et figur med 6, etter Trachtenberg -metoden. Kilde: f. Zapata.

- Multiplikasjon med 7

-Legg nuller til begynnelsen og på slutten av figuren for å multiplisere.

-Dupliser hvert siffer og legg til den nedre halvdelen av naboen, men hvis sifferet er i tillegg til 5.

Eksempel på multiplikasjon med 7

-Multipliser 3412 med 7

-Resultatet er 23884. For å bruke reglene anbefales det først å gjenkjenne de rare sifrene og plassere en liten 5 for å huske å legge til dette tallet til resultatet.

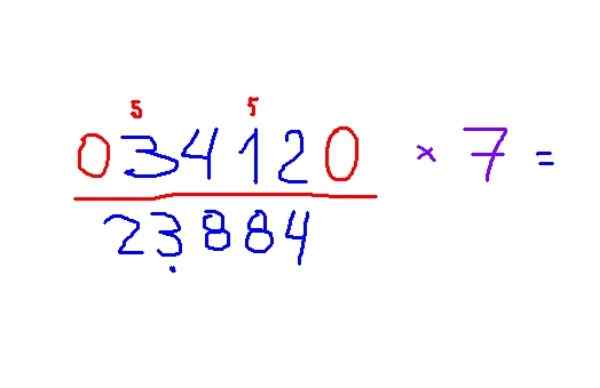Figur 4. Eksempel multiplikasjon av et figur med 7, i henhold til Trachtenbergs metode. Kilde: f. Zapata.

- Multiplikasjon med 5

-Legg nuller til begynnelsen og på slutten av figuren for å multiplisere.

-Plasser under hvert siffer den nedre halvdelen av naboen til høyre, men hvis sifferet er merkelig i tillegg 5.

Eksempel av multiplikasjon med 5

Multipliser 256413 med 5

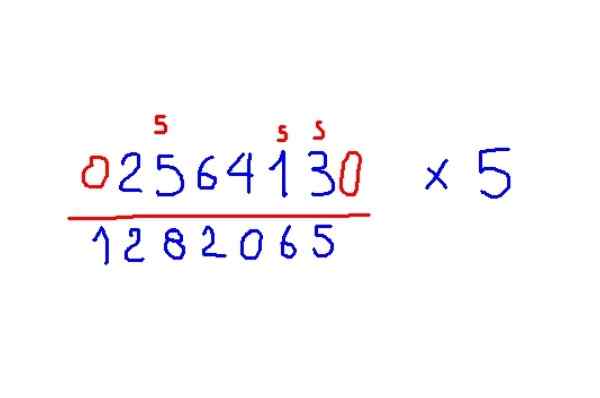Figur 5. Eksempel multiplikasjon av et figur med 5, i henhold til Trachtenberg -metoden. Kilde: f. Zapata.

Regler for produkter innen 9

-En null legges til begynnelsen og en annen på slutten av figuren for å multiplisere med ni.

-Det første sifferet til høyre oppnås ved å trekke fra det tilsvarende sifferet til figuren for å multiplisere.

-Deretter trekkes neste sifferet og naboen blir lagt til.

-Det forrige trinnet gjentas til du når null av multipliseringen, der vi trekker 1 fra naboen og resultatet kopieres under null.

Kan tjene deg: hva er delingene av 30? (Forklaring)

Eksempel på multiplikasjon med 9

Multipliser 8769 med 9:

087690 x 9 =

--

78921

Operasjoner

10 - 9 = 1

(9-6) + 9 = 12 (De 2 Og det tar 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Multiplikasjon med 8, 4, 3 og 2

-Legg nuller til begynnelsen og på slutten av figuren for å multiplisere.

-For det første sifferet til høyre fra 10 og resultatet er doblet.

-For følgende sifre trekker fra 9, blir resultatet doblet og naboen legges til.

-Når du når null, trekke fra 2 fra høyre til høyre.

- Multiplikasjon med 8

Eksempel på multiplikasjon med 8

-Multipliser 789 med 8

Figur 6. Eksempel multiplikasjon av et figur med 8, i henhold til Trachtenberg -metoden. Kilde: f. Zapata.

- Multiplikasjon med 4

-Legg nuller til høyre og venstre for å multiplisere.

-Trekk fra 10 det tilsvarende sifferet til enheten som legger til 5 hvis det er et merkelig siffer.

-Trekk fra 9 i form av hvert multipliserende siffer, tilsett halvparten av naboen til høyre, og hvis det er et merkelig siffer å legge til 5 i tillegg.

-Når du når null i begynnelsen av multipliserende sted halvparten av naboen, bortsett fra en.

Eksempel på multiplikasjon med 4

Multipliser 365187 x 4

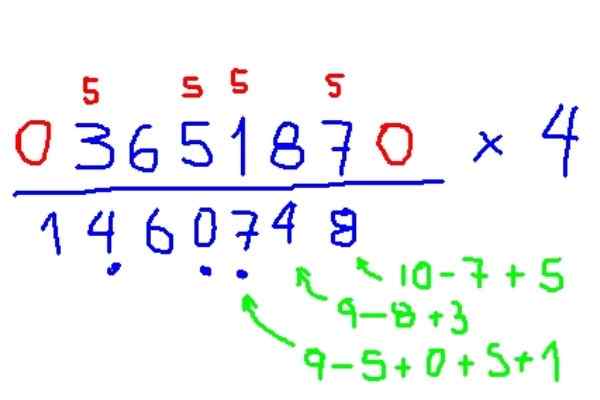Figur 7. Eksempel multiplikasjon av et figur med 4, i henhold til Trachtenberg -metoden. Kilde: f. Zapata.

- Multiplikasjon med 3

-Legg til null i hver ende av multiplisering.

-Trekk fra 10 bortsett fra enhetens siffer og legg til 5 hvis det er et merkelig siffer.

-For de andre sifrene, trekk 9 dupliser resultatet, tilsett halvparten av naboen og tilsett 5 hvis det er rart.

-Når du når null av overskriften, plasser hele halvparten av naboen minus 2.

Eksempel på multiplikasjon med 3

Multipliser 2588 med 3

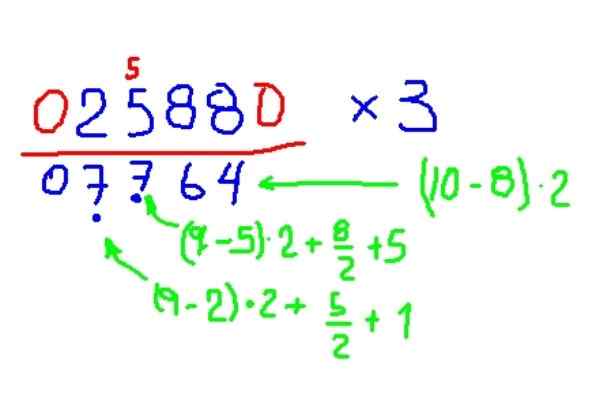Figur 8. Eksempel multiplikasjon av en figur med 3, i henhold til Trachtenberg -metoden. Kilde: f. Zapata.

- Multiplikasjon med 2

-Legg nuller til endene og doble hvert siffer, hvis du overstiger 10, legg til det neste.

Eksempel av multiplikasjon med 2

Multipliser 2374 med 2

023740 x 2

04748

Multipliser med sammensatte figurer

Reglene som er beskrevet ovenfor, brukes, men resultatene går til venstre for antall steder som tilsvarer titalls, hundrevis og så videre. La oss se på følgende eksempel:

Trening 

Multipliser 37654 med 498

0376540 x 498

301232 Rule for 8

338886 Rule for 9

150616 Rule for 4

18751692 Endelig sum

Referanser

1. Cutler, Ann. 1960.Trachtenberg Speed ​​System of Basic Mathematics. Doubleday & Co, NY.
2. Dialnet. Rask grunnleggende matematikksystem. Gjenopprettet fra: Dialnet.com
3. Matematisk hjørne. Rask multiplikasjon etter Trachtenbergs metode. Gjenopprettet fra: Rinconmatematisk.com
4. Trachtenberg Speed ​​System of Basic Mathematics. Gjenopprettet fra: TrachtenbergspeedMath.com
5. Wikipedia. Trachtenberg -metoden. Gjenopprettet fra: Wikipedia.com