Imaginære tallegenskaper, applikasjoner, eksempler

De Imaginære tall De er de som gir løsning på ligningen der den ukjente, firkantede, er lik et reelt negativt tall. Den imaginære enheten er I = √ (-1).

I ligningen: z²= - a, z Det er et tenkt tall som kommer til uttrykk som følger:

 Z = √ (-a) = i√ (a)

Å være til Et positivt reelt tall. Ja A = 1, så z = i, hvor Yo er den imaginære enheten.

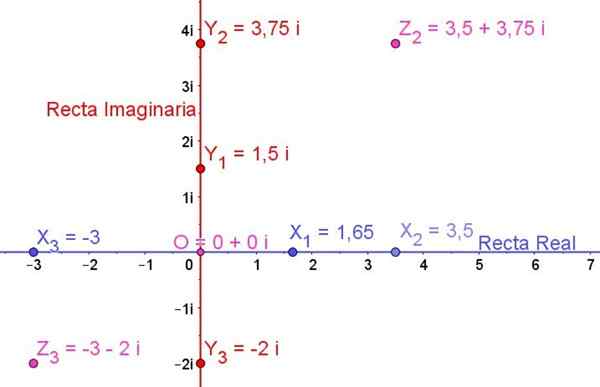Figur 1. Kompleks plan som viser noen reelle tall, noen imaginære tall og noen komplekse tall. Kilde: f. Zapata.

Generelt kommer et tenkt tall Z alltid uttrykt i form: 

z = y⋅i

Hvor og Det er et reelt tall og Yo er den imaginære enheten.

Så vel som reelle tall er representert på en linje, kalt Ekte rett, Analog de imaginære tallene er representert på Imaginær rett.

De Imaginær rett Det er alltid ortogonal (90º form) til Ekte rett og de to linjene definerer et kartesisk plan kalt Kompleks plan.

Figur 1 viser det komplekse planet og noen reelle tall, noen imaginære tall og også noen komplekse tall er representert på det:

X₁, X₂, X₃ De er reelle tall

OG₁, OG₂, OG₃ De er imaginære tall

Z₂ og z₃ De er komplekse tall

Antallet eller er den virkelige null og er også den imaginære null, slik at opprinnelsen eller er nullkomplekset uttrykt av:

0 + 0i 

[TOC]

Egenskaper

Settet med imaginære tall er betegnet med:

I = …, -3i,…, -2i, .. .,-Yo, .. .,0i, .. .,Yo, .. .,2i, .. .,3i, ...

Og noen operasjoner om dette numeriske settet kan defineres. Et imaginært tall oppnås ikke alltid fra disse operasjonene, så vi vil se dem med litt mer detaljer:

Sum og subtraksjon av imaginær

Imaginære tall kan legge til og trekke fra hverandre, og som et resultat vil det være et nytt imaginært tall. For eksempel:

Kan tjene deg: relative søskenbarn: hva er, forklaring, eksempler

 3i + 2i = 5i

4i - 7i = -3i

Imaginært produkt

Når produktet av et tenkt tall med et annet blir gjort, er resultatet et reelt tall. La oss gjøre følgende operasjon for å sjekke:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

Og som vi ser, er -6 et reelt tall, selv om det er oppnådd ved å multiplisere to rene imaginære tall.

Produkt av et reelt tall for et annet imaginært

Hvis et reelt tall multipliseres med i, vil resultatet være et tenkt tall, som tilsvarer en 90 graders rotasjon.

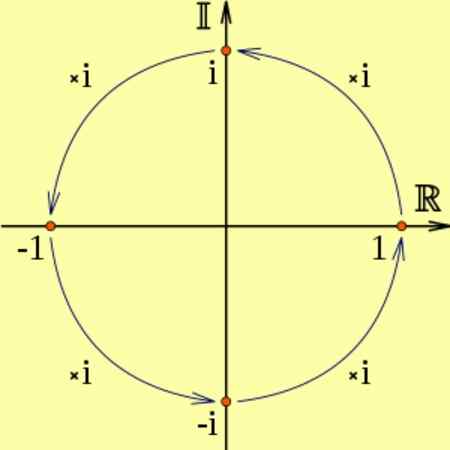
Og er det jeg² tilsvarer to påfølgende rotasjoner på 90 grader, noe som tilsvarer å multiplisere med -1, det vil si i² = -1. Det kan sees i følgende diagram:

Figur 2. Multiplikasjonen med den imaginære enheten og tilsvarer 90º rotasjoner. Kilde: Wikimedia Commons.

For eksempel:

-3 x 5i = -15i

-3 x i = -3i.

Potensiering av en tenkt

Potensieringen av et tenkt tall til en hel eksponent kan defineres:

Yo¹ = jeg

Yo² = i x i = √ (-1) x √ (-1) = -1

Yo³ = i x i² = -I

Yo⁴ = jeg² x i² = -1 x -1 = 1

Yo⁵ = i x i⁴ = jeg

Generelt må du Yoⁿ = i^(n mod 4), hvor Mod Det er resten av divisjonen mellom n og 4.

Potensieringen av negative heltall kan også lages:

Yo^-1 = 1 / i¹ = jeg / (i x i¹) = I / (i²) = I / (-1) = -i

Yo-² = 1 / i² = 1/ (-1) = -1

Yo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Generelt sett er det imaginære tallet B⋅i forhøyet til kraft n:

(B⋅i) iⁿ = bⁿ Yoⁿ = bⁿ i^(n mod 4)

Noen eksempler er følgende:

(5 i)¹² = 5¹² Yo¹² = 5¹² Yo⁰ = 5¹² x 1 = 244140625

(5 i)^elleve = 5^elleve Yo^elleve = 5^elleve Yo³ = 5^elleve x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Yo¹⁰ = 2¹⁰ Yo² = 1024 x (-1) = -1024

Sum av et reelt tall og ett tenkt

Når et reelt tall legges til med et tenkt, er resultatet verken ekte eller imaginært, det er en ny type nummer som heter Komplekst tall.

For eksempel, hvis x = 3,5 og y = 3,75i, er resultatet det komplekse tallet:

Kan tjene deg: minimums torg

Z = x + y = 3,5 + 3,75 i

Merk at de virkelige og imaginære delene ikke kan grupperes i summen, så et komplekst antall alltid vil ha en virkelig del og en annen imaginær del.

Denne operasjonen utvider settet med reelle tall til det bredeste av komplekse tall.

applikasjoner

Navnet på imaginære tall ble foreslått av den franske matematikeren René Descartes (1596-1650) som en hån eller uenighet med forslaget fra dem laget av den italienske matematikeren i Raffelle Century Bombelli.

Andre store matematikere, som Euler og Leibniz, sekunderte Descartes i denne uenigheten og kalte imaginære tall som Amfibiske tall, som ble diskutert mellom å være og intet.

Navnet på imaginære tall opprettholdes i dag, men dets eksistens og betydning er veldig reell og følbar, siden de vises naturlig på mange fysikkfelt som:

-Relativitetsteorien.

-I elektromagnetisme.

-Kvantemekanikk.

Trening med imaginære tall

- Oppgave 1

Finn løsningene av følgende ligning:

z² + 16 = 0

Løsning

z² = -16

Å ta kvadratrot i begge medlemmene du har:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = I x 4 = 4i

Med andre ord, løsningene av den opprinnelige ligningen er:

z = +4i eller z = -4i.

- Oppgave 2

Finn resultatet av å heve imaginær enhet til kraft 5 minus subtraksjon Den imaginære enheten hevet til kraft -5.

Løsning

Yo⁵ - Yo-⁵ = jeg⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Øvelse 3

Finn resultatet av følgende operasjon:

(3i)³ + 9i 

Løsning

3³ Yo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Oppgave 4

Finn løsningene av følgende kvadratiske ligning:

Kan tjene deg: eksistens og unikhet teorem: demonstrasjon, eksempler og øvelser

(-2x)² + 2 = 0

Løsning

Ligningen omorganiseres som følger:

(-2x)² = -2

Ta deretter en kvadratrot i begge medlemmene

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Da oppnås x endelig:

x = ± √2 / 2 i

Det vil si at det er to mulige løsninger:

x = (√2 / 2) i

Eller denne andre:

x = - (√2 / 2) i

- Oppgave 5

Finn verdien av Z definert av:

Z = √ (-9) √ (-4) + 7

Løsning

Vi vet at kvadratroten til et negativt reelt tall er et tenkt tall, for eksempel √ (-9) er lik √ (9) x √ (-1) = 3i.

På den annen side er √ (-4) lik √ (4) x √ (-1) = 2i.

Slik at den opprinnelige ligningen kan erstattes av:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Oppgave 6

Finn verdien av Z som følge av følgende inndeling av to komplekse tall:

Z = (9 - i²) / (3 + i)

Løsning

Ekspresjonsverdatoren kan faktorere ved bruk av følgende egenskap:

En forskjell på firkanter er produktet av summen etter forskjellen på binomialene uten å heve torget.

Så:

Z = [(3 - i) (3 + i)] / (3 + i)

Det resulterende uttrykket blir deretter forenklet ved å være igjen

Z = (3 - i)

Referanser

1. Jarl, r. Komplekse tall. Gjenopprettet fra: Matematikk.okse.Ac.Storbritannia.
2. Figuera, J. 2000. Matematikk 1. Diversifisert. Co-bo-utgaver.
3. Hoffmann, J. 2005. Valg av matematikkproblemer. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Imaginært nummer. Hentet fra: i.Wikipedia.org