Karakteristiske primtall, eksempler, øvelser

De primtall, Også kalt absolutte søskenbarn, er de naturlige tallene som bare er delbare med hverandre og 1. I denne kategorien kommer tall som: 2, 3, 5, 7, 11, 13, 17, 19, 23 og mange flere i denne kategorien.

På den annen side er et sammensatt tall delbart av seg selv, med 1 og minst ett nummer til. Vi har for eksempel 12, som er delbar med 1, 2, 4, 6 og 12. Etter stevne er ikke 1 inkludert i listen over primtall eller i forbindelsene.

Figur 1. Noen primtall. Kilde: Wikimedia Commons.

Kunnskapen om primtallene stammer fra eksterne tider; De gamle egypterne håndterte dem allerede og var sikkert kjent lenge før.

Disse tallene er veldig viktige, siden ethvert naturlig tall kan representeres av produktet av primtall, er denne unike representasjonen, bortsett fra i rekkefølgen av faktorene.

Dette faktum er fullt etablert i et teorem som heter Det grunnleggende teoremet til aritmetikk, som sier at tallene som ikke er søskenbarn, nødvendigvis består av tallprodukter som er.

[TOC]

Kjennetegn på primtall

Under hovedegenskapene til primtallene:

-De er uendelige, siden hvor stort primtall alltid kan bli funnet.

-Hvis et primtall p deler ikke nøyaktig til et annet tall til, Det sies det da p og til De er søskenbarn med hverandre. Når dette skjer, er den eneste vanlige divisoren begge 1.

Det er ikke nødvendig å til Være absolutt fetter. For eksempel er de 5 fetter, og selv om de 12 ikke er, er begge tallene søskenbarn med hverandre, siden de to har en vanlig divisor til 1.

-Når et primtall p Del en kraft av nummeret n, Det deler også en n. Tenk på 100, som er en kraft på 10, spesielt 10². Det hender at de 2 deler både 100 og 10.

-Alle primtall er rare bortsett fra 2, derfor er deres siste siffer 1, 3, 7 eller 9. De 5 er ikke inkludert, for selv om det er merkelig og fetter, er det aldri den endelige figuren av et annet primtall. Faktisk er alle tallene som ender i 5 multipler av dette, og er derfor ikke søskenbarn.

Kan tjene deg: sentral symmetri: egenskaper, eksempler og øvelser

-Ja p Det er fetter og deling av produktet av to tall til.b, så p Del en av dem. For eksempel deler Prime nummer 3 produktet 9 x 11 = 99, siden 3 er en divisor på 9.

Hvordan vite om et tall er fetter

De PRIMALITET Det er navnet gitt til kvaliteten på å være fetter. Vel, fransk matematisk Fermats lille teorem, Som sier det:

"Gitt et fetter naturlig nummer p og ethvert naturlig tall til større enn 0, er det oppfylt det til^p - til Det er et multiplum av p, så lenge som p være fetter ".

Vi kan bekrefte dette ved hjelp av små tall, for eksempel anta P = 4, At vi allerede vet at det ikke er fetter og A = 6:

6⁴ - 6 = 1296 - 6 = 1290

Tallet 1290 er ikke akkurat delbart mellom 4, derfor er ikke 4 et primtall.

La oss gjøre testen nå med p = 5, som er fetter og a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 er delbar mellom 5, siden et hvilket som helst tall som slutter 0 eller 5 er. Faktisk 7760/5 = 1554. Ettersom Fermats lille teorem er oppfylt, kan vi sikre at 5 er et primtall.

Testen gjennom teoremet er effektiv og direkte med lite tall, der operasjonen er enkel å utføre, men hva de skal gjøre hvis de ber oss om å finne ut primaliteten til et stort antall?

I så fall deles antallet suksessivt mellom alle mindre primtall, inntil en eller annen eksakt inndeling eller at kvotienten er mindre enn divisoren.

Hvis noen divisjon er nøyaktig, betyr det at antallet er sammensatt, og hvis kvotienten er mindre enn divisoren, betyr det at antallet er fetter. Vi vil utføre det i praksis i året løst 2.

Måter å finne et primtall

Det er uendelige primtall, og det er ingen unik formel for å bestemme dem. Imidlertid observerer noen primtall som disse:

Kan tjene deg: Nullvinkel: Definisjon og egenskaper, eksempler, øvelser

3, 7, 31, 127 ..

Det observeres at de er i form 2ⁿ - 1, med n = 2, 3, 5, 7, 9 ... Vi forsikrer deg:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Men vi kan ikke forsikre at generelt 2ⁿ - 1 være fetter, fordi det er noen verdier av n som det ikke fungerer, for eksempel på 4:

2⁴ - 1 = 16 - 1 = 15

Og nummer 15 er ikke fetter, siden det ender på 5. Et av de største primtallⁿ - 1 med:

N = 57.885.161

De Mersenne Formula forsikrer oss om at 2^p - 1 er alltid fetter, så lenge som p Vær også fetter. For eksempel er 31 fetter, så det er sikkert at 2³¹ - 1 Det er også:

2³¹ - 1 = 2.147.483.647

Imidlertid tillater formelen bare noen primtall å bestemmes, ikke alle.

Eulers formel

Følgende polynom gjør det mulig å finne primtall så lenge n er mellom 0 og 39:

P (n) = n² + N + 41

Senere, i delen Løste øvelser er det et eksempel på bruken av den.

ERATOSTENES -screening

Eratóstenes var en kroppsbygning og matematisk av det gamle Hellas som bodde i det tredje århundre til.C. Han utviklet en grafisk metode for å finne primtallene som vi kan utføre med små tall, det kalles Eratóstenes -skjermen (en skjerm er som en sil).

-Tallene er plassert i et bord som det som er vist i animasjonen.

-Da er de jevnt tallene merket, bortsett fra de to som vi vet er fetter. Alle andre er multipler av dette, og derfor er de ikke søskenbarn.

-Multiplene på 3, 5, 7 og 11 er også merket, unntatt dem alle fordi vi vet at de er søskenbarn.

-Multiplene på 4, 6, 8, 9 og 10 er allerede merket, fordi de er forbindelser og derfor multipler av noen av søskenbarnene som er angitt.

Kan tjene deg: Historie med trigonometri fra dens opprinnelse

-Endelig er de gjenværende tallene umerket er søskenbarn.

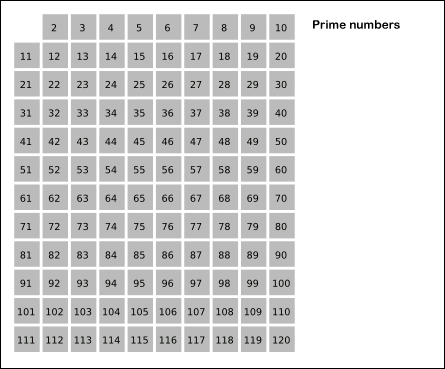Figur 2. Eratostenes screening animasjon. Kilde: Wikimedia Commons.

Øvelser

- Oppgave 1

Ved å bruke Euler -polynomet for primtall, finn 3 tall større enn 100.

Løsning

Dette er polynomet som Euler foreslo å finne primtall, som fungerer for N -verdier mellom 0 og 39.

P (n) = n² + N + 41

Gjennom Tanteo velger vi en verdi av n, for eksempel n = 8:

P (8) = 8² + 8 + 41 = 113

Ettersom n = 8 produserer et primtall større enn 100, evaluerer vi deretter polynomet for n = 9 og n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Oppgave 2

Finn ut om følgende tall er søskenbarn:

a) 13

b) 191

Løsning på

De 13 er små nok til å bruke Fermats lille teorem og hjelp av kalkulatoren.

Vi bruker A = 2 slik at tallene ikke er for store, selv om de også kan brukes A = 3, 4 eller 5:

2^{1. 3} - 2 = 8190

8190 er delbar mellom 2, siden det er til og med, derfor er 13 fetter. Leseren kan bekrefte den ved å gjøre den samme testen med A = 3.

Løsning b

191 er veldig stor for å prøve teoremet og en felles kalkulator, men vi kan rette inndelingen mellom hvert primtall. Vi utelater å dele med 2 fordi 191 ikke engang er og divisjonen ikke vil være nøyaktig eller forholdet mindre enn 2.

Vi prøvde å dele med 3:

191/3 = 63.666 ..

Og det gir ikke nøyaktig, og heller ikke kvotienten er mindre enn divisoren (63.666 ... er større enn 3)

Vi fortsetter å teste 191 av søskenbarnene 5, 7, 11, 13 og den eksakte divisjonen er ikke nådd, og heller ikke forholdet mindre enn divisoren. Til den deler seg mellom 17:

191/17 = 11, 2352 ..

Siden det ikke er nøyaktig og 11.2352 ... det er mindre enn 17, er tallet 191 fetter.

Referanser

1. Baldor, a. 1986. Aritmetikk. Codex -utgaver og distribusjoner.
2. Prieto, c. Primo -tall. Hentet fra: sider.Matem.Unam.MX.
3. Egenskaper for primtall. Gjenopprettet fra: Mae.Ufl.Edu.
4. Smartick. Primo -tall: Hvordan finne dem med silen til eratostener. Gjenopprettet fra: Smartick.er.
5. Wikipedia. primtall. Gjenopprettet fra: er.Wikipedia.org.