Firkantet prisme

Vi forklarer hva

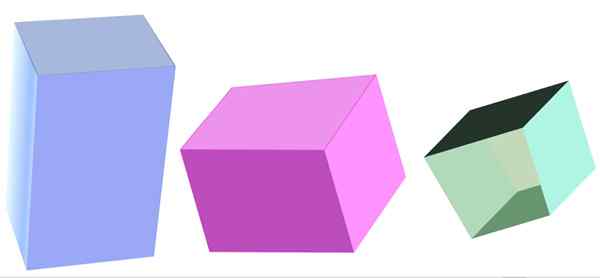
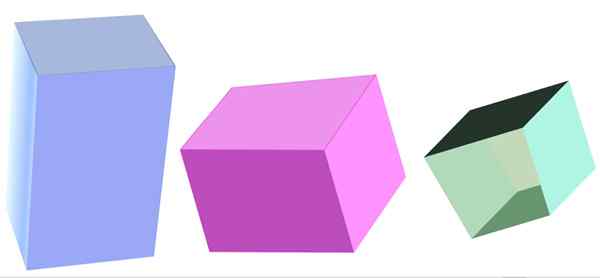Ulike typer firkantet prisme. Kilde: f. Zapata

Hva er et firedelt prisme?

Han Firkantet prisme Det er en tre -dimensjonal geometrisk figur av Polyhedros -familien. Den består av to likeverdige og parallelle ansikter, med formen som en firkantet, som en base, og fire parallellogrammer på sidene, i totalt seks ansikter.

Det er flere kriterier for å klassifisere dem, siden det er mange muligheter for form av ansikter og tilbøyeligheter. For eksempel er det Rette hjemmekjørte prismer og skråstilte firkantede prismer.

I det første tilfellet er sidene vinkelrett på basen, og så er de rektangler eller firkanter. I det andre tilfellet er sideflatene tilbøyelig med hensyn til basen, derfor kan de ikke være rektangler eller firkantede.

I tillegg kan firkantet prisme være regelmessig eller uregelmessig, avhengig av basen er en vanlig eller uregelmessig firkantet. Den vanlige kvadrilaterale er torget, hvis fire sider og dens fire vinkler måler det samme .

Et eksempel på spesiell hjemmekjørt prisme er den parallellepipede, hvis baser er parallellogrammer. Formene på boksene og mursteinene er inspirert av firkantede prismer, så gode eksempler på hvordan du bruker denne geometriske figuren i praktiske anvendelser er.

Kjennetegn på det kvadrangulære prisme

Blant de viktigste egenskapene til det kvadrangulære prisme er følgende:

• Ansiktene deres har en polygonform.
• Den har totalt 6 ansikter (2 baser og 4 sider), 12 kanter eller kanter og 8 hjørner (hjørner).
• Side ansiktene kan formes som: firkant, rektangel, parallellogram, rhombus eller rhomboid.
• Sidene kan være rette (form 90º vinkel med basene) eller skrå (det er en vinkel mindre enn 90º på den indre siden).
• Siden ansiktene til rette prismer kan bare være firkantede eller rektangler.
• Prismbasene mottar også navnet på retningslinjer.
• Hvis basen er en vanlig firkantet, er også det firedoblede prisme. Ettersom en flat figur er regelmessig hvis alle sidene har samme tiltak, er den eneste muligheten at basene er firkantede.
• Når prismebunnen er noe annet firkantet forskjellig fra torget, blir prisme ansett som uregelmessig.
• Det vanlige firkantede prisme kan registreres i en sylinder.

Kan tjene deg: Inferensiell statistikk: Historie, egenskaper, hva er det for, eksempler

Elementer i det firedoblede prisme

De fem elementene i det kvadrangulære prisme er felles for alle prismer:

• Baser, konstituert av to identiske og parallelle firkantede.
• Laterale ansikter, er de fire parallellogrammer som grenser til figuren.
• Hjørner eller hjørner, vanlige punkter som har tre tilstøtende sider av prisme.
• Kanter eller kanter, vanlig segment som har to tilstøtende ansikter.
• Høyde: Det er lengden på et vinkelrett segment med ender i basene. Når prisme er rett, sammenfaller høyden med målet på sidekantene.
• Rett seksjon, Kryssområde mellom prisme og et fly som danner 90º med sidekantene.

Følgende bilde viser hvert av disse elementene for et rett kvadrangulært prisme:

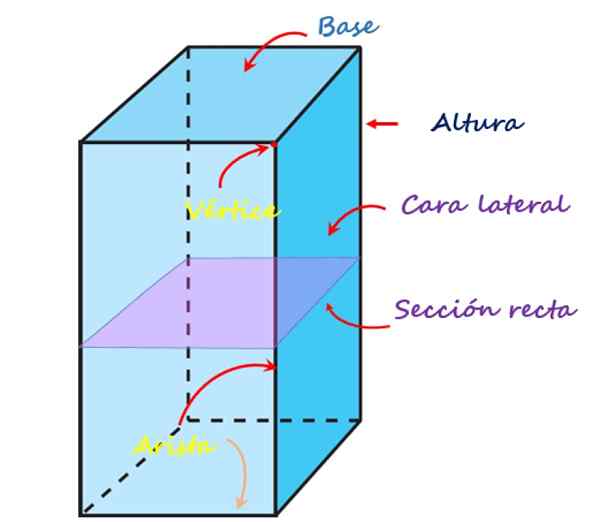Elementene i det firedoblede prisme. Kilde: f. Zapata

Ansikter, hjørner og kanter

Av stor betydning å studere det firkantede prisme er ansiktene, toppunktene og kantene:

Ansikter

Ansiktene til prisme utgjør totalt 6: de to identiske basene i form av en firedobling og 4 sidesider eller ansikter i form av parallellogram.

Hjørner

De er hjørnene på figuren, punktet der tre tilstøtende ansikter kommer.

Kanter

De er kryssets segmenter mellom prisme ansiktene. Kantene er klassifisert som:

• Basiskanter, Vanlige segmenter mellom baser og sideflater.
• Laterale kanter, Som navnet tilsier, er de de vanlige segmentene blant sideflatene.

Den øverste figuren viser de to typene kanter, utpekt med piler med forskjellige farger. Antall kanter n_TIL kan bestemmes med Euler Teorem av polyhedrosene, som knytter antall kanter til ansiktene n n_C og hjørner n_V:

Kan tjene deg: matematiske funksjoner

N_TIL = N_C + N_V −2

For det firedoblede prisme n_C = 6 og n_V = 8, derfor:

N_TIL = 6 + 8 −2 = 12

Derfor er antallet kanter eller kanter på det firkantede prisme 12.

Hvordan beregne volumet til et firkantet prisme?

Prismens volum forstås som den delen av plassen som er låst av det, og måles i kubiske enheter, som kan være kubikkmeter, kubikkcentimeter, kubikkfot eller annet passende, forutsatt at de har lengde til kuben.

Volum V er alltid en positiv mengde, og i tilfelle av kvadrangulært prisme er det gitt av produktet mellom basen til basen til_b og høyde H:

V = a_b × H

Yo) Vanlig firkantet prismevolum

Siden basene er firkantet, og kvadratet på torget er dens side ℓ kvadrat:

TIL_b = ℓ²

Deretter er volumet av prisme hvis høyde er "H":

V = ℓ² × H

) Uregelmessig firkantet prismevolum

Det avhenger av formen på basen og høyden "H" i prisme:

1.- Rektangulært baseprisme

Området til sidene rektangel "A" og "B" er:

TIL_b = A × B

Så volumet er:

V = a × b × h

2.- Romboidal Base Prism

Rhombusområdet er semiproduktet fra "D" og "D" -diagonaler:

Og volumet er:

3.- Romboid -formet baseprisme

Det rhomboid -formede baseområdet er et produkt av basen "B" og dens relative høyde "h_r”Til denne basen, som er det vinkelrett segmentet som går fra denne basen til parallellsiden til det.

TIL_b = B × H_r

Derfor er prismeens volum med denne basen:

Kan tjene deg: Hva er statistikkområdet? (Med eksempler)

V = b × h_r × H

4.- Trapezoidal baseprisme

Siden området til trapesformet er semi -stedet for de parallelle sidene "A" og "B", multiplisert med høyden "C":

Volumet av det trapesformet prisme er:

5.- Trapezoid -formet baseprisme

Området til en symmetrisk trapesoid er halvproduktet til diagonalene d og d, derfor:

I dette tilfellet er prismeens volum:

Trening løst

En trapesformet base firedelt prisme har et volum på 648 cm³. De parallelle sidene av trapezoid mål A = 10 cm og B = 5 cm, mens høyden på trapesen er C = 6 cm. Med disse dataene finn høyden på prisme.

Løsning

Siden dimensjonene til basen har, kan området ditt enkelt beregnes:

Og av formelen:

V = a_b × H

“H” er ryddet, høyden på prisme, siden volumet er kjent:

H = v/ a_b = 648 cm³ / 45 cm² = 14.4 cm

Eksempler

Rektangulært prisme eller kube

De seks ansiktene til dette rette prisme er firkantet eller rektangulært. Boksene er eksempler på rektangulære prismer, en form som også brukes i mange gjenstander og konstruksjoner som bygninger.

Kube

En kube er et vanlig firkantet prisme, hvis seks sider er formet som en firkant, for eksempel en terning eller det kjente Rubiks kubespill.

Kuben er en del av gruppen av platoniske faste stoffer, geometriske figurer som oppfyller to forhold. Det første er at hvert ansikt er en vanlig polygon, og det andre er at hvert toppunkt har til felles samme antall ansikter.

Kuben oppfyller begge forholdene, ettersom ansiktene deres har en firkantet form, som er en vanlig polygon. Og i hver av de åtte hjørnene til kuben er tre ansikter av samme konvergering.

De gjenværende platoniske faste stoffer er tetrahedronen, oktaedronen, dodekaedroen og icosaedro.